Con uno dei metodi visti si stabilisce che la conica è una parabola non degenere. Cominciamo col trasformare l'equazione in una del tipo
Y = AX2 + BX + C
mediante una rotazione degli assi cartesiani, le cui equazioni sono del tipo:
![]()
Sostituendo nell'equazione di partenza ed imponendo che si annullino i coefficienti di Y2 e XY si ottiene
![]()
e scegliendo, per esempio,
![]()
si ottiene l'equazione Y=X2+2X, che ha il vertice nel punto V=(-1;-1); basterà ora eseguire la traslazione che porti l'origine degli assi cartesiani in V: X=x'-1, Y=y'-1.
Si ottiene l'equazione y'=(x')2, che è la forma canonica
richiesta.
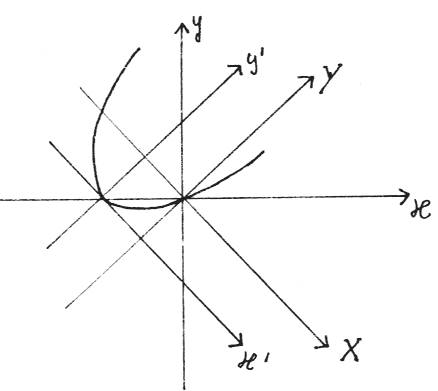
E' anche possibile determinare il vertice e l'asse di una generica parabola: dopo averla trasformata in una con asse parallelo all'asse delle ordinate, si trovano il vertice e l'asse rispetto al nuovo sistema di riferimento e, mediante la rotazione inversa, si possono ottenere vertice ed asse nel sistema di riferimento di partenza.
Si verifica facilmente che la conica è un'ellisse reale non degenere. Si esegue una traslazione di assi in modo che la conica venga ad avere il centro nell'origine:
x=X+a', y=Y+b';
si sostituisce nell'equazione di partenza e si impone che si annullino i termini di primo grado in X ed Y; si ottiene:
a' = 8/3, b' = 4/3;
la nuova equazione è:
X2 - XY + Y2 - 16/3 = 0
(notare come i coefficienti dei termini di secondo grado non cambino).
Si esegue ora una rotazione che porti ad annullare il termine XY:
(*) ![]()
sostituendo nell'equazione in X, Y ed annullando il termine in x'y' si ottiene
![]()
e scegliendo, per esempio, il valore positivo si arriva alla forma canonica
3(x') 2 + 9(y') 2 = 32
N.B.
Si può dimostrare che il valore di alfa che annulla il coefficiente di XY è quello per cui
![]()
(cotg è la cotangente)
con b non nullo (se b=0 manca già il termine xy nell'equazione di partenza!)
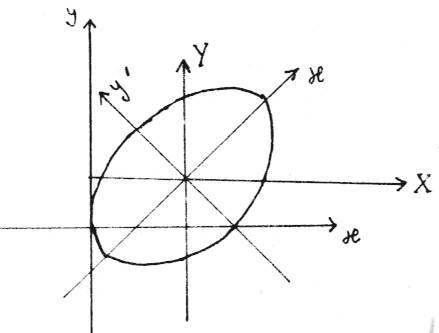
Notare come il procedimento utilizzato permetta anche di trovare il centro e gli assi della conica.