Le coniche da un punto di vista geometrico

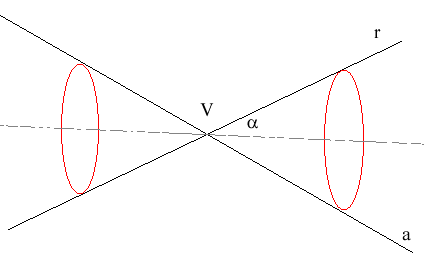
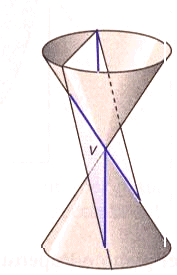
Chiamiamo "cono circolare retto" la superficie generata dalla rotazione di una retta r intorno ad un'altra retta a (asse di rotazione) incidente ad r. Il punto V di intersezione tra r ed a è detto "vertice" del cono; l'angolo a formato da r con a (minore di un angolo retto) è detto "apertura" del cono.

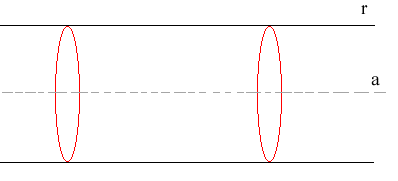
Se r è parallela ad a la superficie ottenuta si chiama "cilindro circolare retto", che può intendersi come particolare cono (si dice che il vertice è all'infinito).

DEF. 1.1 Si chiama conica la curva ottenuta intersecando un cono circolare retto con un piano.

Detto b l'angolo formato dal piano secante con l'asse di rotazione del cono distinguiamo i seguenti tipi di coniche:

1) Piano non passante per il vertice:

    a) b>a: ellisse (reale non degenere)

         Il piano taglia solo una delle due falde del cono.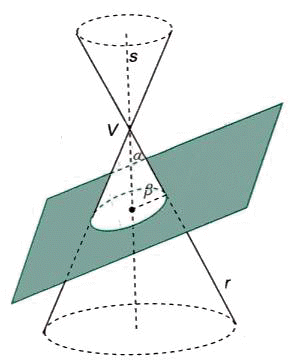

        Nel caso particolare in cui b è retto abbiamo la circonferenza.

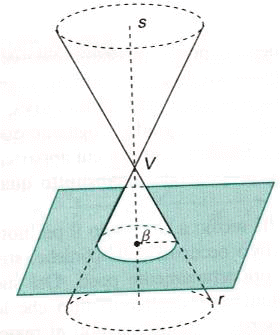
b) b=a: parabola (reale non degenere).

            Il piano taglia il cono lungo una sola falda.

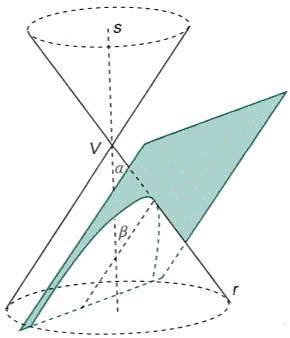
       b) b<a: iperbole (reale non degenere).

            Il piano taglia il cono lungo le due falde.

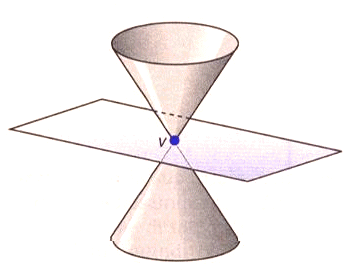
2) Piano passante per il vertice:

     a) b>a: conica degenere in un punto (detta di tipo ellittico).

           L'intersezione si riduce al solo vertice.

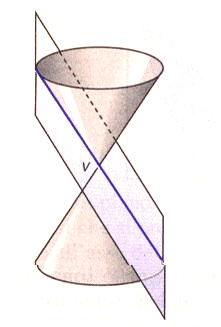
      b) b=a: conica degenere in due rette coincidenti (detta di tipo parabolico).

           Il piano è tangente al cono.

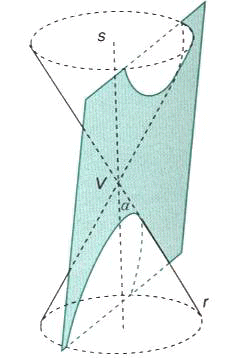
     c) b<a: conica degenere in due rette reali distinte incidenti ( tipo iperbolico).

           L'intersezione si riduce a due generatrici distinte del cono

3) Il cono ha il vertice all'infinito (cilindro):

   a) il piano non taglia il cilindro: conica immaginaria.

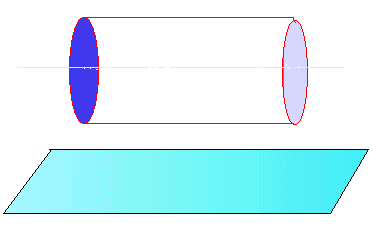
    b) il piano taglia il cilindro ed è parallelo all'asse di rotazione: conica degenere in due rette distinte parallele.

    Riepilogando si presentano i seguenti tipi di coniche:

a) CONICHE REALI NON DEGENERI

   1) Ellisse (circonferenza)

    2) Parabola

    3) Iperbole

b) CONICHE REALI DEGENERI

   4) In un punto (tipo ellittico)

    5) In due rette reali distinte parallele (tipo parabolico) o incidenti (tipo iperbolico)

    6) In due rette reali coincidenti (tipo parabolico)

c) CONICA IMMAGINARIA

   7) Ellisse immaginaria (perchè, come vedremo, rientra nel tipo ellittico).

Osservazione

Un qualsiasi cono retto ammette come sezioni tutte le possibili ellissi e parabole ma non tutte le iperboli (solo quelle i cui asintoti formano un angolo non superiore all'angolo di apertura del cono).