ALTRA FORMA DEL QUINTO POSTULATO

Prima di addentrarci nelle dispute intorno al quinto postulato domostriamo l'equivalenza tra la forma data da Euclide e quella (forse più nota) secondo cui:

postulato 5': "Per un punto esterno ad una retta passa una sola parallela ad una retta data".

Ricordiamo che l'esistenza di una parallela ad una retta data per un punto ad essa esterno viene dimostrata da Euclide nella proposizione 31 (si costruiscono due angoli alterni interni uguali....).

Con la proposizione 30 si dimostra la cosiddetta proprietà comparativa del parallelismo, ovvero che: "le parallele ad una stessa retta sono parallele fra loro" ( per la dimostrazione si sfrutta il fatto che due rette parallele formano con una trasversale angoli alterni interni uguali e viceversa).

Dimostriamo che da postulato 5 segue il postulato 5':

se per un punto P esterno ad una retta a passassero due rette parallele ad a queste dovrebbero essere tra di loro parallele ( in base alla prop. 30); ma avendo un punto in comune, P, sono coincidenti.

Dimostriamo che dal postulato 5' segue il postulato 5:

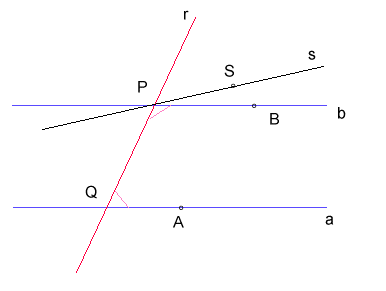
Vogliamo dimostrare che se due rette tagliate da una trasversale formano angoli coniugati interni la cui somma è minore di due retti, allora le due rette si incontrano.

Supponiamo che le due rette siano parallele; esiste per P una retta s tale che insieme ad a e alla trasversale r forma angoli coniugati interni supplementari; ma allora, per la prop. 28 (dimostrata, ricordiamolo, senza ricorrere al quinto postulato) segue che s è parallela ad a; ma anche b è parallela ad a e pertanto, per il postulato 5' s deve coincidere con b; ma allora a e b formano con la trasversale r angoli coniugati interni la cui somma è due angoli retti, mentre per ipotesi la loro somma è minore di due angoli retti; allora non può essere b parallela ad a e quindi ne segue la tesi.