IL TENTATIVO DI P. SACCHERI

Il gesuita italiano pensò di dimostrare il quinto postulato a contrariis: sia questo postulato ciò che bisogna dimostrare; si assuma a punto di partenza la negazione di esso; se questa negazione, nel corso del procedimento dimostrativo, si distrugge da sé, essa risulterà falsa e quindi il postulato, che costituisce il suo contrario, risulterà vero.

Sta di fatto che egli pose a punto di partenza due ipotesi negative del quinto postulato che "dimostrò" inconsistenti solo perché non coerenti con l'impianto sistematico della stessa geometria euclidea. Ma quelle due ipotesi suggerirono ai matematici dell'Ottocento la via per dimostrare non solo che il quinto postulato era indimostrabile, ma che era possibile costruire su di esse delle nuove geometrie "non euclidee".

Seguiamo, a grandi linee, il ragionamento che Saccheri ha esposto nell'opera "Euclide emendato da ogni macchia" (Euclides ab omni naevo vindicatus).

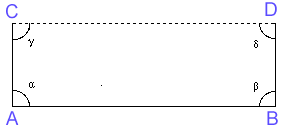
Sia un segmento AB; dagli estremi si elevino due segmenti perpendicolari di uguale grandezza tra loro, AC e BD; si congiunga C con D. Gli angoli alfa e beta sono uguali e retti; si verifica facilmente che anche gli angoli gamma e delta saranno anch'essi uguali tra loro (basta considerare le coppie di triangoli congruenti ABC e ABD e successivamente la coppia di triangoli ADC e ACB che risultano anch'essi congruenti).

Ma tali angoli saranno anche retti?

Secondo il postulato di Euclide, sí (prima ipotesi). Assumiamo ora le due ipotesi opposte a quel postulato: cioè quella per cui essi sono entrambi ottusi (seconda ipotesi), e quella per cui sono entrambi acuti (terza ipotesi). Nell'ipotesi dell'angolo ottuso, gli angoli gamma e delta saranno ognuno maggiore di un angolo retto; nell'ipotesi dell'angolo acuto, essi saranno entrambi minori di un angolo retto. È chiaro che se si assume l'ipotesi dell'angolo retto, allora vale la conclusione che la somma degli angoli interni di un triangolo è uguale a due angoli retti; ma se si assume quella dell'angolo ottuso, essa sarà sempre maggiore di due retti, e se si ammette quella dell'angolo acuto, essa sarà sempre minore di due retti.

Si esamini dunque la validità della seconda ipotesi; il quinto postulato non è per sé incompatibile con essa; allora dovrebbero valere anche i teoremi connessi a quel postulato; tra questi c'è quello per cui la somma degli angoli di un quadrilatero è uguale a quattro retti; ma nell'ipotesi dell'angolo ottuso la somma degli angoli del quadrilatero sarà di necessità maggiore di quattro retti; allora la seconda ipotesi si distrugge da sé e decade.

In realtà tale ipotesi non era decaduta, perché Saccheri non ha dimostrato incoerenza tra conseguenze e premesse assunte in via ipotetica, ma solo l'incompatibilità tra l'ipotesi ammessa e le conseguenze connesse all'ipotesi euclidea.

Saccheri poi dimostra l'insostenibilità dell'ipotesi dell'angolo acuto, ma commette un errore, in quanto estende all'infinito una proprietà che è valida al finito (per un punto esterno ad una retta si può tracciare una sola perpendicolare ad una retta data).