LICEO SCIENTIFICO 2025 - OORDINAMENTO

LICEO SCIENTIFICO 2025 - PROBLEMA 1

Soluzione proposta da Giuseppe Scoleri con la collaborazione di Angela Santamaria.

"La ragione non è nulla senza l'immaginazione" - Cartesio

Dato \(r > 0\) e \(k < 0\), si considerino la circonferenza \(C_r\), di centro l'origine e raggio \(r\), e la funzione \(f_k(x) = k|x|\).

a)

Verificare che \(f_k\) è continua ma non derivabile in \(x=0\) qualunque sia il valore di \(k\). Individua i due valori di \(r\) in corrispondenza dei quali \(C_r\) delimita con il grafico di \(f_k\), per valori opportuni di \(k\), un settore circolare nel semipiano \(y \le 0\) di area \(\pi\) e contorno di lunghezza \(4+\pi\). Stabilito che \(r=2\) è il maggiore di tali valori, in uno stesso riferimento cartesiano \(OXY\), tracciare la circonferenza \(C_2\) e il grafico della funzione \(f_{-1}\).

Soluzione del punto a

Studio della continuità di \( f_k(x) = k|x| \), con \( k < 0 \), in \( x=0 \):

La funzione \(f_k(x) = k|x|\) può essere riscritta come:

\[ f_k(x) = \begin{cases} kx & \text{se } x \ge 0 \\ -kx & \text{se } x < 0 \end{cases} \]

Per verificare la continuità in \(x=0\), dobbiamo controllare che il limite della funzione per \(x \to 0\) sia uguale al valore della funzione in \(x=0\).

\[ \lim_{x \to 0^+} f_k(x) = \lim_{x \to 0^+} (kx) = k \cdot 0 = 0 \] \[ \lim_{x \to 0^-} f_k(x) = \lim_{x \to 0^-} (-kx) = -k \cdot 0 = 0 \]

E il valore della funzione in \(x=0\) è:

\[ f_k(0) = k|0| = 0 \]

Poiché \(\lim_{x \to 0^+} f_k(x) = \lim_{x \to 0^-} f_k(x) = f_k(0) = 0\), la funzione \(f_k(x)\) è **continua in \(x=0\) per qualunque valore di \(k\)**.

Studio della derivabilità in \( x=0 \):

Calcoliamo la derivata di \(f_k(x)\) per \(x \ne 0\):

\[ f'_k(x) = \begin{cases} k & \text{se } x > 0 \\ -k & \text{se } x < 0 \end{cases} \]

Ora calcoliamo i limiti del rapporto incrementale o, equivalentemente, i limiti della derivata da destra e da sinistra in \(x=0\):

\[ \lim_{x \to 0^+} f'_k(x) = k \] \[ \lim_{x \to 0^-} f'_k(x) = -k \]

Poiché \(k < 0\), \(k\) è un valore negativo e \(-k\) è un valore positivo. Quindi, \(k \ne -k\).

Essendo i limiti delle derivate destra e sinistra diversi (e finiti), e poiché la funzione è continua in \(x=0\), possiamo affermare che la funzione \(f_k(x)\) **non è derivabile in \(x=0\) per alcun valore di \(k < 0\)**.

Rappresentazione della circonferenza e della funzione:

Ecco una rappresentazione grafica generica della circonferenza \(C_r: x^2+y^2=r^2\) e della funzione \(f_k(x) = k|x|\) (una 'V' rovesciata, dato \(k<0\)).

[Image of Grafico di Circonferenza e Funzione]

Ricerca dei punti di intersezione \(A\) e \(B\) tra \(f_k\) e \(C_r\):

Dobbiamo mettere a sistema le equazioni della circonferenza \(C_r: x^2+y^2=r^2\) e della funzione \(f_k(x) = k|x|\) (ovvero \(y = k|x|\)).

Sostituendo \(y = k|x|\) nella prima equazione, otteniamo:

\[ x^2 + (k|x|)^2 = r^2 \] \[ x^2 + k^2x^2 = r^2 \] \[ x^2(1+k^2) = r^2 \] \[ x^2 = \frac{r^2}{1+k^2} \] \[ x = \pm \sqrt{\frac{r^2}{1+k^2}} = \pm \frac{r}{\sqrt{1+k^2}} \]

Chiamiamo \(x_A = - \frac{r}{\sqrt{1+k^2}}\) e \(x_B = \frac{r}{\sqrt{1+k^2}}\).

Ora troviamo le corrispondenti ordinate \(y\). Poiché \(y=k|x|\) e \(k<0\), la \(y\) sarà sempre negativa. Per \(x_B = \frac{r}{\sqrt{1+k^2}}\) (che è positivo), \(y_B = k \left| \frac{r}{\sqrt{1+k^2}} \right| = \frac{kr}{\sqrt{1+k^2}}\). Per \(x_A = - \frac{r}{\sqrt{1+k^2}}\) (che è negativo), \(y_A = k \left| - \frac{r}{\sqrt{1+k^2}} \right| = k \frac{r}{\sqrt{1+k^2}} = \frac{kr}{\sqrt{1+k^2}}\).

Quindi i punti di intersezione sono:

\[ A \left( -\frac{r}{\sqrt{1+k^2}}, \frac{kr}{\sqrt{1+k^2}} \right) \quad \text{e} \quad B \left( \frac{r}{\sqrt{1+k^2}}, \frac{kr}{\sqrt{1+k^2}} \right) \]

Calcolo dell'area del settore circolare:

L'area del settore circolare è \(A = \frac{1}{2} r^2 \Phi\), dove \(\Phi\) è l'angolo al centro totale del settore circolare (ovvero l'angolo \(A\hat{O}B\)).

Consideriamo la metà dell'angolo al centro, che chiamiamo \(\alpha\). Data la simmetria del grafico di \(f_k(x)\) rispetto all'asse \(y\), questo angolo \(\alpha\) corrisponde all'angolo \(H\hat{O}B\), dove \(H\) è la proiezione del punto \(B\) sull'asse \(y\) (quindi \(H\) ha coordinate \((0, y_B)\)).

Nel triangolo rettangolo formato dall'origine \(O\), dal punto \(B(x_B, y_B)\) e dalla sua proiezione \(H(0, y_B)\) sull'asse \(y\), l'angolo \(H\hat{O}B\) ha tangente:

\[ \tan(H\hat{O}B) = \frac{\text{cateto opposto (segmento HB)}}{\text{cateto adiacente (segmento OH)}} = \frac{|x_B|}{|y_B|} \]

Sostituendo le coordinate di \(B\):

\[ \tan(H\hat{O}B) = \frac{r/\sqrt{1+k^2}}{-kr/\sqrt{1+k^2}} = \frac{1}{-k} \]

Dunque, l'angolo \(\alpha\) (cioè \(H\hat{O}B\)) è tale che \(\tan \alpha = \frac{1}{-k}\). Poiché \(k<0\), \(-k>0\), quindi \(\alpha\) è un angolo acuto.

\[ \alpha = \arctan\left(-\frac{1}{k}\right) \]

L'angolo totale al centro \(\Phi\) è il doppio di \(\alpha\):

\[ \Phi = 2\alpha = 2 \arctan\left(-\frac{1}{k}\right) \]

L'area del settore circolare è quindi:

\[ A = \frac{1}{2} r^2 \Phi = \frac{1}{2} r^2 \cdot \left( 2 \arctan\left(-\frac{1}{k}\right) \right) = r^2 \arctan\left(-\frac{1}{k}\right) \]

Sappiamo che l'area è \(\pi\), quindi:

\[ r^2 \arctan\left(-\frac{1}{k}\right) = \pi \quad (*) \]

Calcolo della lunghezza del contorno:

Il contorno è formato dai due segmenti \(OA\) e \(OB\) e dall'arco di circonferenza \(AB\).

Lunghezza dei segmenti \(OA\) e \(OB\): \(OA = OB = r\) (sono raggi della circonferenza).

Lunghezza dell'arco \(AB = r \cdot \Phi = r \cdot 2 \arctan\left(-\frac{1}{k}\right)\).

Quindi la lunghezza totale del contorno è:

\[ L = OA + OB + \text{arco } AB = r + r + r \cdot 2 \arctan\left(-\frac{1}{k}\right) = 2r + 2r \arctan\left(-\frac{1}{k}\right) \]

Sappiamo che la lunghezza del contorno è \(4+\pi\), quindi:

\[ 2r + 2r \arctan\left(-\frac{1}{k}\right) = 4+\pi \quad (**) \]

Ora abbiamo un sistema di due equazioni con due incognite (\(r\) e \(k\)):

\(r^2 \arctan\left(-\frac{1}{k}\right) = \pi\)
\(2r + 2r \arctan\left(-\frac{1}{k}\right) = 4+\pi\)

Dalla prima equazione, possiamo ricavare \(\arctan\left(-\frac{1}{k}\right) = \frac{\pi}{r^2}\).

Sostituiamo questo nella seconda equazione:

\[ 2r + 2r \left(\frac{\pi}{r^2}\right) = 4+\pi \] \[ 2r + \frac{2\pi}{r} = 4+\pi \]

Moltiplichiamo tutto per \(r\) (dato che \(r>0\)):

\[ 2r^2 + 2\pi = (4+\pi)r \]

Riorganizziamo in una equazione quadratica in \(r\):

\[ 2r^2 - (4+\pi)r + 2\pi = 0 \]

Calcoliamo il discriminante \(\Delta\):

\[ \Delta = (-(4+\pi))^2 - 4(2)(2\pi) = (4+\pi)^2 - 16\pi \] \[ \Delta = 16 + 8\pi + \pi^2 - 16\pi = 16 - 8\pi + \pi^2 = (4-\pi)^2 \]

Ora calcoliamo i valori di \(r\):

\[ r = \frac{(4+\pi) \pm \sqrt{(4-\pi)^2}}{2 \cdot 2} = \frac{(4+\pi) \pm |4-\pi|}{4} \]

Poiché \(\pi \approx 3.14\), \(4-\pi > 0\), quindi \(|4-\pi| = 4-\pi\).

Primo valore di \(r\):

\[ r_1 = \frac{(4+\pi) - (4-\pi)}{4} = \frac{4+\pi-4+\pi}{4} = \frac{2\pi}{4} = \frac{\pi}{2} \]

Secondo valore di \(r\):

\[ r_2 = \frac{(4+\pi) + (4-\pi)}{4} = \frac{4+\pi+4-\pi}{4} = \frac{8}{4} = 2 \]

I due valori di \(r\) sono \(\frac{\pi}{2}\) e \(2\). Il problema dice di stabilire che \(r=2\) è il maggiore di tali valori. Essendo \(\frac{\pi}{2} \approx \frac{3.14}{2} = 1.57\), **\(r=2\) è il maggiore**.

Ora dobbiamo trovare il valore opportuno di \(k\) per ciascun \(r\). Usiamo l'equazione \(\arctan\left(-\frac{1}{k}\right) = \frac{\pi}{r^2}\).

Per \(r=2\):

\[ \arctan\left(-\frac{1}{k}\right) = \frac{\pi}{2^2} = \frac{\pi}{4} \] \[ -\frac{1}{k} = \tan\left(\frac{\pi}{4}\right) \] \[ -\frac{1}{k} = 1 \] \[ k = -1 \]

Questo valore di \(k\) è accettabile, in quanto \(k<0\).

Per \(r=\frac{\pi}{2}\):

\[ \arctan\left(-\frac{1}{k}\right) = \frac{\pi}{(\pi/2)^2} = \frac{4\pi}{\pi^2} = \frac{4}{\pi} \] \[ -\frac{1}{k} = \tan\left(\frac{4}{\pi}\right) \] \[ k = - \frac{1}{\tan\left(\frac{4}{\pi}\right)} \]

Dato che \(\frac{4}{\pi} \approx \frac{4}{3.14} \approx 1.27\). Questo valore è in radianti. \(1.27\) rad è circa \(1.27 \cdot \frac{180}{\pi} \approx 72.8^\circ\). \(\tan(72.8^\circ)\) è positivo, quindi \(k\) sarà negativo, il che è coerente con \(k<0\).

Soluzione alternativa per la ricerca dei due valori del raggio della circonferenza

Vediamo come si può trovare il raggio di una circonferenza conoscendo il perimetro \(2p\) e l'area \(S\) di un suo settore circolare. Nel nostro caso, indicata con \( l \) la lunghezza dell'arco \( AB \):

\[ 2p = 4 + \pi \quad \text{da cui:} \quad l + 2r = 4 + \pi \] \[ S = \pi \]

Dalla geometria ricordiamo che:

\[ S = \frac{1}{2} \cdot l \cdot r \]

Dobbiamo quindi risolvere il seguente sistema:

\[ \begin{cases} l = 4 + \pi - 2r \\ l \cdot r = 2\pi \end{cases} \]

Sostituiamo \( l \) dalla prima equazione nella seconda:

\[ (4 + \pi - 2r) \cdot r = 2\pi \] \[ (4 + \pi)r - 2r^2 = 2\pi \] \[ 2r^2 - (4 + \pi)r + 2\pi = 0 \]

Abbiamo ottenuto una equazione di secondo grado in \(r\). Calcoliamo il discriminante:

\[ \Delta = (4 + \pi)^2 - 4 \cdot 2 \cdot 2\pi = (4 + \pi)^2 - 16\pi \] \[ \Delta = 16 + 8\pi + \pi^2 - 16\pi = 16 - 8\pi + \pi^2 = (4 - \pi)^2 \]

Le soluzioni sono:

\[ r = \frac{(4 + \pi) \pm \sqrt{(4 - \pi)^2}}{4} = \frac{(4 + \pi) \pm |4 - \pi|}{4} \]

Poiché \(4 > \pi\), abbiamo \(|4 - \pi| = 4 - \pi\):

Prima soluzione:

\[ r_1 = \frac{(4 + \pi) + (4 - \pi)}{4} = \frac{8}{4} = 2 \]

Seconda soluzione:

\[ r_2 = \frac{(4 + \pi) - (4 - \pi)}{4} = \frac{2\pi}{4} = \frac{\pi}{2} \]

Il più grande valore di \(r\) è quindi \(2\), come richiesto. Osserviamo che con \(r = 2\) si ottiene:

\[ l = 4 + \pi - 2r = 4 + \pi - 2(2) = 4 + \pi - 4 = \pi \]

L'angolo al centro del settore circolare è quindi:

\[ \Phi = \frac{l}{r} = \frac{\pi}{2} \]

Essendo l'angolo \(\Phi\) retto, osservando la figura deduciamo che \(k = -1\).

Tracciare la circonferenza \(C_2\) e il grafico della funzione \(f_{-1}\):

Per \(r=2\), la circonferenza \(C_2\) ha equazione \(x^2+y^2=2^2\), cioè \(x^2+y^2=4\).

Per \(k=-1\), la funzione è \(f_{-1}(x) = -1|x|\), ovvero \(y = -|x|\).

Questa funzione si scompone in:

\[ y = \begin{cases} -x & \text{se } x \ge 0 \\ x & \text{se } x < 0 \end{cases} \]

Il grafico di \(y=-|x|\) è una "V" rovesciata con vertice nell'origine, con pendenza \(-1\) per \(x>0\) e pendenza \(1\) per \(x<0\).

Il grafico mostra la circonferenza di raggio 2 e la funzione \(y=-|x|\). I punti di intersezione sono \((-\sqrt{2}, -\sqrt{2})\) e \((\sqrt{2}, -\sqrt{2})\)

Il grafico richiesto è il seguente.

[Image of Grafico Circonferenza e Funzione per r=2 e k=-1]

b)

Studiare la funzione \(g(x) = \sqrt{4-x^2}\), specificandone dominio, simmetrie, punti di non derivabilità, intervalli di monotonia ed insieme immagine. Verificare che il grafico di \(g\) coincide con la parte di \(C_2\) che si trova nel semipiano \(y \ge 0\). Spiegare perché \(g\) non è derivabile nel suo dominio ed esplicitare l'intervallo \([a; b]\) di ampiezza massima, con \(b>0\), nel quale \(g\) ammette una funzione inversa \(h\). Qual è l'espressione analitica di \(h\)?

Soluzione del punto b

Studio della funzione \(g(x) = \sqrt{4-x^2}\):

Dominio:

La funzione \(g(x)\) è definita se l'argomento della radice quadrata è non negativo:

\[ 4-x^2 \ge 0 \] \[ x^2 \le 4 \] \[ -2 \le x \le 2 \]

Il dominio della funzione è \([-2, 2]\).

Simmetrie:

Verifichiamo se la funzione è pari o dispari. Calcoliamo \(g(-x)\):

\[ g(-x) = \sqrt{4-(-x)^2} = \sqrt{4-x^2} \]

Poiché \(g(-x) = g(x)\), la funzione è **pari**. Il suo grafico è simmetrico rispetto all'asse \(y\).

Limiti:

La funzione è continua in un intervallo chiuso e limitato \([-2, 2]\), quindi non è necessario calcolare limiti all'infinito o ai bordi del dominio per la continuità. Calcoliamo i valori agli estremi del dominio:

\[ g(-2) = \sqrt{4-(-2)^2} = \sqrt{4-4} = 0 \] \[ g(2) = \sqrt{4-2^2} = \sqrt{4-4} = 0 \]

Punti di non derivabilità:

Calcoliamo la derivata prima di \(g(x)\) per \(x \in (-2, 2)\):

\[ g'(x) = \frac{d}{dx} (4-x^2)^{1/2} = \frac{1}{2}(4-x^2)^{-1/2} (-2x) = \frac{-x}{\sqrt{4-x^2}} \]

La derivata prima \(g'(x)\) non è definita per \(x=\pm 2\), poiché il denominatore si annulla. Verifichiamo il comportamento della derivata in questi punti calcolando i limiti:

Per \(x \to -2^+\):

\[ \lim_{x \to -2^+} g'(x) = \lim_{x \to -2^+} \frac{-x}{\sqrt{4-x^2}} = \frac{-(-2)}{\sqrt{4-((-2)^+)^2}} = \frac{2}{0^+} = +\infty \]

Per \(x \to 2^-\):

\[ \lim_{x \to 2^-} g'(x) = \lim_{x \to 2^-} \frac{-x}{\sqrt{4-x^2}} = \frac{-2}{\sqrt{4-(2^-)^2}} = \frac{-2}{0^+} = -\infty \]

Poiché i limiti delle derivate sono infinito, i punti \(x=-2\) e \(x=2\) sono **punti a tangente verticale**, quindi punti di non derivabilità

Intervalli di monotonia:

Studiamo il segno della derivata prima \(g'(x) = \frac{-x}{\sqrt{4-x^2}}\) nell'intervallo \((-2, 2)\).

Il denominatore \(\sqrt{4-x^2}\) è sempre positivo in \((-2, 2)\). Quindi il segno di \(g'(x)\) dipende solo dal segno del numeratore \(-x\).

\[ -x > 0 \implies x < 0 \] \[ -x < 0 \implies x > 0 \]

Quindi:

Per \(-2 < x < 0\), \(g'(x) > 0\), la funzione è **crescente**.
Per \(0 <x < 2\), \(g'(x) < 0\), la funzione è **decrescente**.

In \(x=0\), la funzione ha un **massimo relativo e assoluto**. Il valore del massimo è \(g(0) = \sqrt{4-0^2} = 2\). Nei punti \((-2, 0)\) e \((2, 0)\) c'è il minimo assoluto.

L'insieme immagine della funzione è \([0, 2]\).

Verifica che il grafico di \(g\) coincide con la parte di \(C_2\) che si trova nel semipiano \(y \ge 0\):

L'equazione della circonferenza \(C_2\) con centro nell'origine e raggio \(r=2\) è \(x^2+y^2=2^2\), ovvero \(x^2+y^2=4\).

Se esplicitiamo \(y\) da questa equazione, otteniamo \(y^2 = 4-x^2\), da cui \(y = \pm \sqrt{4-x^2}\).

La funzione \(g(x) = \sqrt{4-x^2}\) rappresenta solo la **semicirconferenza superiore** (quella con \(y \ge 0\)) della circonferenza \(C_2\).

Questo è coerente con il dominio \([-2, 2]\) e l'insieme immagine \([0, 2]\) di \(g(x)\).

Spiegazione del perché \(g\), come già visto, non è derivabile in non è derivabile nel suo dominio ed esplicitazione dell'intervallo \([a; b]\) di ampiezza massima, con \(b>0\), nel quale \(g\) ammette una funzione inversa \(h\). Qual è l'espressione analitica di \(h\)?

La funzione \(g(x)\) non è derivabile su tutto il suo dominio \([-2, 2]\) perché, come già visto, non è derivabile in -2 e 2. Per ammettere una funzione inversa, una funzione deve essere **iniettiva** nel suo intervallo. La funzione \(g(x)\), essendo pari e avendo intervalli di crescita e decrescita (crescente in \([-2, 0]\) e decrescente in \([0, 2]\)), non è iniettiva sul suo intero dominio \([-2, 2]\).

Per trovare un intervallo \([a; b]\) di ampiezza massima con \(b>0\) in cui \(g\) ammette una funzione inversa \(h\), dobbiamo scegliere un intervallo in cui \(g\) sia **strettamente monotona**. I due intervalli massimi di stretta monotonia sono \([-2, 0]\) (dove \(g\) è crescente) e \([0, 2]\) (dove \(g\) è decrescente).

Poiché il problema richiede che sia \(b>0\), scegliamo l'intervallo \([0, 2]\). In questo intervallo, \(g(x)\) è strettamente decrescente e quindi iniettiva, ammettendo una funzione inversa.

Per trovare l'espressione analitica di \(h(y)\), scambiamo \(x\) e \(y\) nell'equazione \(y = \sqrt{4-x^2}\) e risolviamo per \(x\):

\[ y = \sqrt{4-x^2} \]

Eleviamo al quadrato entrambi i membri (tenendo presente che \(y \ge 0\) dall'immagine di g):

\[ y^2 = 4-x^2 \] \[ x^2 = 4-y^2 \] \[ x = \pm \sqrt{4-y^2} \]

Dato che abbiamo scelto l'intervallo \([0, 2]\) per \(x\) (dove \(x \ge 0\)), dobbiamo prendere la radice positiva.

\[ x = \sqrt{4-y^2} \]

Quindi, l'espressione analitica della funzione inversa \(h\) è:

\[ h(x) = \sqrt{4-x^2} \]

Il dominio di \(h(x)\) è l'immagine di \(g(x)\) sull'intervallo \([0, 2]\), che è \([0, 2]\). L'immagine di \(h(x)\) è il dominio scelto di \(g(x)\), che è \([0, 2]\).

Si noti che l'espressione analitica di \(h(x)\) è la stessa di \(g(x)\) quando ristretta all'intervallo \([0, 2]\). Questo è vero perché, nel quadrante positivo, la semicirconferenza è simmetrica rispetto alla bisettrice \(y=x\).

Il grafico di \(g(x)\) (che è la semicirconferenza superiore) è il seguente:

c)

Sia A un punto del grafico di \(g\), situato nel primo quadrante, e siano M e R le sue proiezioni ortogonali sugli assi di riferimento. Determinare le coordinate di A in modo che il quadrilatero AMOR abbia area massima. Dopo aver verificato che tale quadrilatero è un quadrato, dimostrare che è anche quello di perimetro massimo.

Soluzione del punto c

Il grafico della funzione \(g(x)=\sqrt{4-x^2}\) (semicirconferenza superiore di raggio 2) nel primo quadrante e il quadrilatero AMOR sono rappresentati di seguito:

[Image of Grafico con punti A, M, R, O per il problema c]

Sia \(A\) un punto del grafico di \(g\) nel primo quadrante. Le sue coordinate sono \(A(x_A, y_A)\).

Poiché \(A\) si trova sul grafico di \(g(x)\) e nel primo quadrante, le sue coordinate sono \(A(t, \sqrt{4-t^2})\), con \(t > 0\).

Essendo \(A\) nel primo quadrante, \(x_A = t\) e \(y_A = \sqrt{4-t^2}\), con \(0 \le t \le 2\).

Dalla figura segue che le coordinate di M e di R sono le seguenti:

\(M\) sull'asse \(x\): \(M(t, 0)\)
\(R\) sull'asse \(y\): \(R(0, \sqrt{4-t^2})\)

L'origine è \(O(0, 0)\).

Calcolo dell'area del quadrilatero AMOR in funzione di \(t\):

Il quadrilatero AMOR è un rettangolo, poiché i suoi vertici sono \(O(0,0)\), \(M(t,0)\), \(A(t, \sqrt{4-t^2})\) e \(R(0, \sqrt{4-t^2})\), e gli assi di riferimento sono perpendicolari.

L'area di un rettangolo è data dal prodotto della base per l'altezza. In questo caso, la base è \(OM = t\) e l'altezza è \(OR = \sqrt{4-t^2}\).

\[ A(AMOR) = f(t) = OM \cdot OR = t \cdot \sqrt{4-t^2} \]

Il dominio di \(f(t)\) è \([0, 2]\), come dedotto dal dominio di \(g(x)\) nel primo quadrante.

Cerchiamo il massimo di \(y=f(t)\) in \([0, 2]\):

Per trovare il massimo, calcoliamo la derivata prima di \(f(t)\):

\[ f'(t) = \frac{d}{dt} \left( t \sqrt{4-t^2} \right) \]

Usiamo la regola del prodotto \((uv)' = u'v + uv'\):

\[ u = t \implies u' = 1 \] \[ v = \sqrt{4-t^2} = (4-t^2)^{1/2} \implies v' = \frac{1}{2}(4-t^2)^{-1/2}(-2t) = \frac{-t}{\sqrt{4-t^2}} \] \[ f'(t) = 1 \cdot \sqrt{4-t^2} + t \cdot \frac{-t}{\sqrt{4-t^2}} \] \[ f'(t) = \sqrt{4-t^2} - \frac{t^2}{\sqrt{4-t^2}} \]

Mettiamo a denominatore comune:

\[ f'(t) = \frac{(4-t^2) - t^2}{\sqrt{4-t^2}} = \frac{4-2t^2}{\sqrt{4-t^2}} \]

Per trovare i punti stazionari, poniamo \(f'(t) = 0\):

\[ 4-2t^2 = 0 \] \[ 2t^2 = 4 \] \[ t^2 = 2 \] \[ t = \pm \sqrt{2} \]

Dato che \(t \in [0, 2]\), consideriamo solo \(t = \sqrt{2}\).

Studiamo il segno di \(f'(t)\):

\[ f'(t) > 0 \implies 4-2t^2 > 0 \implies 2t^2 < 4 \implies t^2 < 2 \implies -\sqrt{2} < t < \sqrt{2} \] \[ f'(t) < 0 \implies 4-2t^2 < 0 \implies 2t^2 > 4 \implies t^2 > 2 \implies t < -\sqrt{2} \text{ o } t > \sqrt{2} \]

Considerando il dominio \([0, 2]\):

Per \(0 \le t \le \sqrt{2}\), \(f'(t) > 0\), la funzione \(f(t)\) è **crescente**.
Per \(\sqrt{2}< t \le 2\), \(f'(t) < 0\), la funzione \(f(t)\) è **decrescente**.

Questo significa che \(t = \sqrt{2}\) è un punto di massimo assoluto per l'area.

Di seguito lo studio del segno della derivata prima e del comportamento di \(f(t)\):

Intervallo	Segno di \( f'(t) \)	Comportamento di \( f(t)\)
\( 0 \le t < \sqrt{2} \)	+	Crescente ↗
\( t = \sqrt{2} \)	0	Massimo ↑
\( \sqrt{2} < t \le 2\)	-	Decrescente ↘

Le coordinate di \(A\) per cui l'area è massima sono \(A(\sqrt{2}, \sqrt{4-(\sqrt{2})^2})\), quindi \(A(\sqrt{2}, \sqrt{4-2})\), ovvero \(A(\sqrt{2}, \sqrt{2})\).

L'area massima è \(f(\sqrt{2}) = \sqrt{2} \cdot \sqrt{4-(\sqrt{2})^2} = \sqrt{2} \cdot \sqrt{2} = 2\).

Verifica che il quadrilatero AMOR di area massima è un quadrato:

Le coordinate di \(A\) per l'area massima sono \(A(\sqrt{2}, \sqrt{2})\).

In questo caso, \(OM = \sqrt{2}\) e \(OR = \sqrt{2}\).

Poiché i lati adiacenti \(OM\) e \(OR\) hanno la stessa lunghezza, e AMOR è un rettangolo, esso è un **quadrato**.

Verifica che quando il quadrilatero AMOR ha area massima ha anche perimetro massimo:

Il perimetro del rettangolo AMOR è \(2p(t) = 2 \cdot (OM + OR)\).

\[ 2p(t) = 2 \cdot (t + \sqrt{4-t^2}) \]

Per trovare il massimo del perimetro, calcoliamo la derivata prima di \(2p(t)\):

\[ (2p)'(t) = 2 \cdot \left( \frac{d}{dt} (t + \sqrt{4-t^2}) \right) \] \[ (2p)'(t) = 2 \cdot \left( 1 + \frac{-t}{\sqrt{4-t^2}} \right) \] \[ (2p)'(t) = 2 \cdot \left( \frac{\sqrt{4-t^2} - t}{\sqrt{4-t^2}} \right) \]

Poniamo \((2p)'(t) = 0\):

\[ \sqrt{4-t^2} - t = 0 \] \[ \sqrt{4-t^2} = t \]

Eleviamo al quadrato entrambi i membri (ricordando che \(t \ge 0\)):

\[ 4-t^2 = t^2 \] \[ 4 = 2t^2 \] \[ t^2 = 2 \] \[ t = \pm \sqrt{2} \]

Dato che \(t \in [0, 2]\), consideriamo solo \(t = \sqrt{2}\).

Studiamo il segno di \((2p)'(t)\). Il denominatore \(\sqrt{4-t^2}\) è positivo. Dobbiamo studiare il segno di \(\sqrt{4-t^2} - t\).

\[ \sqrt{4-t^2} - t > 0 \implies \sqrt{4-t^2} > t \]

Elevando al quadrato (per \(t \ge 0\)):

\[ 4-t^2 > t^2 \] \[ 4 > 2t^2 \] \[ 2 > t^2 \] \[ -\sqrt{2} < t < \sqrt{2} \]

Considerando il dominio \([0, 2]\):

Per \(0 \le t < \sqrt{2}\), \((2p)'(t) > 0\), il perimetro è **crescente**.
Per \(\sqrt{2} < t \le 2\), \((2p)'(t) < 0\), il perimetro è **decrescente**.

Quindi, \(t = \sqrt{2}\) è il valore che massimizza il perimetro. Questo valore coincide con il valore di \(t\) che massimizza l'area.

Dato che il valore di \(t\) per cui il quadrilatero AMOR ha area massima (\(t=\sqrt{2}\)) è lo stesso per cui ha perimetro massimo, la dimostrazione è completa.

Dimostrazione elementare algebrica per la ricerca del rettangolo di area e perimetro massimi:

Osserviamo che il rettangolo AMOR ha diagonale costante \( d=2 \), pari al raggio della semicirconferenza.

La ricerca del rettangolo AMOR di area e perimetro massimi equivale al seguente problema di massimo e minimo di geometria elementare:

Tra tutti i rettangoli di data diagonale \( d \) trovare quello di area massima. Dimostrare che il rettangolo di area massima è anche quello di perimetro massimo.

Indichiamo con \( x \) ed \( y \) le misure dei lati del rettangolo. Nel nostro caso \( x \) ed \( y \) sono le coordinate del punto \( A \) e risulta \( 0 < x < 2 \) e \( 0 < y < 2 \). Inoltre, per il Teorema di Pitagora, si ha: \( x^2+y^2=d^2=4 \).

L'area del rettangolo è \( S= x \cdot y \).

Dalla seguente relazione:

\[ (x-y)^2= x^2+y^2-2xy=d^2 -2xy \] deduciamo che: \[2xy=d^2-(x-y)^2 \] Il secondo membro assume il valore massimo quando \( (x-y)^2 \) assume il valore minimo, cioè quando \( x=y \). Quindi \( 2xy \) è massim0 quando \( x=y \). Ma se è massimo \( 2xy \) è massimo \( xy \), che è l'area del rettangolo. Pertanto: Il rettangolo AMOR ha area massima quando è un quadrato ed essendo \( x^2+y^2=d^2=4 \) si ha \(2x^2=4 \) da cui \( x=y= \sqrt{2} \). Il punto \( A\) in tal caso ha coordinate \(A=(\sqrt{2}, \sqrt{2}) \).

Dimostriamo che quando il rettangolo ha area massima anche il perimetro è massimo

Il perimetro del rettangolo è dato da : \( 2p=2x+2y=2(x+y) \). Il perimetro è massimo se è massimo \( x+y \). Ciò avviene se è massimo \( (x+y)^2 \), essendo \( x+y \) una quantità postiva.

Osserviamo che:

\[ (x+y)^2=x^2+y^2+2xy=d^2+2S \] Deduciamo che \( (x+y)^2 \) è massimo se è massimo \( d^2+2S \). Ma tale espressione, in base a quanto detto sopra, è massima quando \( x=y \).
Concludiamo che:
Il rettangolo di area massima ha anche perimetro massimo

Dimostrazione elementare geometrica per la ricerca del rettangolo di area e perimetro massimi

Dimostriamo per via geometrica che tra tutti i rettangoli di data diagonale il quadrato è quello che ha area massima e perimetro massimo.

Un rettangolo di data diagonale \( d \) possiamo inscriverlo in una circonferenza di diametro pari alla diagonale. Indichiamo con AMOR il rettangolo e iscriviamolo nella circonferenza di diametro \( AO=d \):

[Rettangolo inscritto in circonferenaImage c]

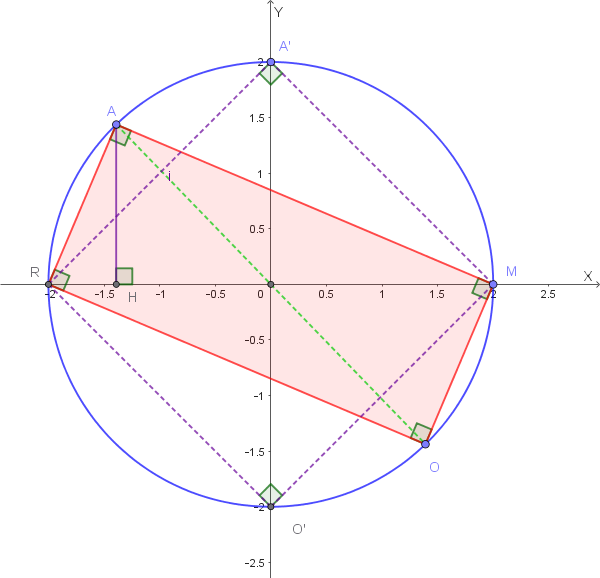
Il rettangolo AMOR ha area massima se ha area massima il triangolo AMR rettangolo in A e di ipotenusa MR uguale al diametro \( d \) della circonferenza; tale triangolo ha infatti area pari alla metà di quella del rettangolo

Il triangolo AMR ha area \( \frac{AM \cdot AH}{2} \). Essendo la base \( AM=d \) costante, tale area è massima se è massima la sua altezza AH. Ma il massimo di AH è il raggio della circonferenza, e ciò si ha quando A coincide con \( A' \).

Ma quando A coincide con \( A' \) risulta \( A'R = A'M \) e quindi il rettangolo AMOR diventa il quadrato A'MO'R: questo dimostra che il rettangolo AMOR di data diagonale ha area massima quando è un quadrato.

Per dimostrare che quando il rettangolo ha area massima anche il perimetro è massimo possiamo ripetere la dimostrazione precedente

d)

Si consideri la funzione \(F(x)=\int_{-2}^{x} \sqrt{4-t^2} \, dt\), con \(x \in [-2;2]\). Determinare \(F(2)\) e tracciare un grafico di \(F\), dopo averne studiato monotonia e concavità. Scrivere, inoltre, l’equazione della retta tangente al grafico di \(F\) nel suo punto di flesso.

Soluzione del punto d

Calcolo di \(F(2)\):

La funzione \(F(x)=\int_{-2}^{x} \sqrt{4-t^2} \, dt\), con \(x \in [-2;2]\).

Per calcolare \(F(2)\), abbiamo:

\[ F(2) = \int_{-2}^{2} \sqrt{4-t^2} \, dt \]

Osserviamo che la funzione integranda \(g(t) = \sqrt{4-t^2}\) rappresenta la semicirconferenza superiore con centro O e raggio 2 . L'integrale definito da -2 a 2 di questa funzione corrisponde all'area del semicerchio di raggio 2.

Quindi, \(F(2)\) è l'area di un semicerchio di raggio \(r=2\).

\[ F(2) = \frac{1}{2} \pi r^2 = \frac{1}{2} \pi (2^2) = \frac{1}{2} \pi \cdot 4 = 2\pi \]

Pertanto, \(F(2) = 2\pi\).

Studio della monotonia di \(F(x)\):

Il dominio di \(F(x)\) è l'intervallo \([-2; 2]\).

Per il Teorema Fondamentale del Calcolo Integrale, la derivata prima di \(F(x)\) è \(F'(x) = \sqrt{4-x^2}\), che è esattamente la funzione \(g(x)\) studiata nel punto precedente.

\[ F'(x) = g(x) = \sqrt{4-x^2} \]

Dal grafico di \(g(x)\) (che è la semicirconferenza superiore), sappiamo che \(g(x) \ge 0\) per ogni \(x\) nell'intervallo \([-2; 2]\). In particolare, \(g(x) > 0\) per \(x \in (-2, 2)\) e \(g(\pm 2) = 0\).

Poiché \(F'(x) = g(x) \ge 0\) per ogni \(x \in [-2; 2]\), la funzione \(F(x)\) è **sempre crescente** sul suo dominio.

Inoltre, calcoliamo il valore di \(F(-2)\):

\[ F(-2) = \int_{-2}^{-2} \sqrt{4-t^2} \, dt = 0 \]

Studio della concavità di \(F(x)\):

Per studiare la concavità di \(F(x)\), analizziamo il segno della sua derivata seconda, che, per il Teorema Fondamentale del Calcolo Integrale, è la derivata prima della funzione integranda \(g(x)\):

\[ F''(x) = g'(x) = \frac{-x}{\sqrt{4-x^2}} \]

Dal punto precedente (Studio della monotonia di \(g(x)\)), sappiamo che:

La funzione \(g(x)\) è crescente per \(-2 < x < 0\), il che implica \(g'(x) > 0\). Pertanto, \(F''(x) > 0\) per \(-2 < x < 0\).
La funzione \(g(x)\) è decrescente per \(0 < x < 2\), il che implica \(g'(x) < 0\). Pertanto, \(F''(x) < 0\) per \(0 < x < 2\).

In \(x=0\), \(F''(x)\) cambia segno, indicando un **punto di flesso**.

L'ordinata del punto di flesso è \(F(0)\):

\[ F(0) = \int_{-2}^{0} \sqrt{4-t^2} \, dt \]

Questo integrale rappresenta l'area del quarto di cerchio nel secondo quadrante con raggio 2.

\[ F(0) = \frac{1}{4} \pi r^2 = \frac{1}{4} \pi (2^2) = \pi \]

Quindi, il punto di flesso è \((0, \pi)\).

Di seguito lo studio della concavità e del punto di flesso:

Intervallo	Segno di \( F''(x) \)	Concavità di \( F(x) \)
\( -2 \le x < 0 \)	+	Concava verso l'alto ↥
\( x = 0 \)	0	Flesso
\( 0 < x \le 2 \)	-	Concava verso il basso ↧

Il grafico di \(F(x)\) è il seguente:

Equazione della retta tangente al grafico di \(F\) nel suo punto di flesso:

Il punto di flesso è \((0, \pi)\).

La pendenza della retta tangente in un punto è data dalla derivata prima della funzione in quel punto. Quindi, la pendenza \(m\) in \(x=0\) è \(F'(0)\).

\[ m = F'(0) = g(0) = \sqrt{4-0^2} = \sqrt{4} = 2 \]

L'equazione della retta tangente a una funzione \(F(x)\) nel punto \((x_0, F(x_0))\) è data da \(y - F(x_0) = F'(x_0)(x - x_0)\).

Sostituendo i valori del punto di flesso \((0, \pi)\) e della pendenza \(m=2\):

\[ y - \pi = 2(x - 0) \] \[ y - \pi = 2x \] \[ y = 2x + \pi \]

Questa è l'equazione della retta tangente al grafico di \(F\) nel suo punto di flesso.