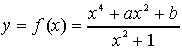
a) Tra le funzioni di equazione

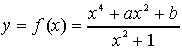
dobbiamo trovare la curva k che soddisfi le seguenti condizioni:

1) tagli la retta di equazione y=1 in due punti distinti e in due punti coincidenti;

2) sia tangente all'asse x in due punti distinti (quattro intersezioni a due a due coincidenti).

Facendo sistema tra y=f(x) e y=1 si ottiene l'equazione risolvente:

che fornisce due soluzioni coincidenti e due distinte solo se b=1 (se il termine noto fosse diverso da zero potremmo avere solo soluzioni distinte, a due a due opposte).

Con b=1 si ha

che, oltre alle due soluzioni coincidenti con x = 0, ha, se a<1, le due soluzioni distinte

Facendo sistema tra y=f(x) e y=0 e tenendo presente che b=1 si ha:

che avrà quattro soluzioni a due a due coincidenti se

di cui, per la precedente condizione sulla a, è accettabile a=-2.

La funzione richiesta ha quindi equazione

• Essa è definita su tutto l'asse reale, è simmetrica rispetto all'asse delle ordinate, essendo

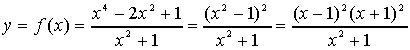
e pertanto, in base alle condizioni precedenti, ha nel punto (0;1), intersezione doppia con la retta di equazione y=1, un massimo relativo e nei punti (-1;0) e (1;0), intersezioni doppie con l'asse x, dei minimi, essendo chiaramente la funzione non negativa.

• I limiti al più infinito e al meno infinito sono uguali a + infinito; non esistono asintoti obliqui, essendo la funzione un infinito del secondo ordine all'infinito.

• La derivata prima è:

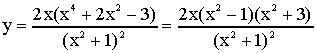
che si annulla per x=0, x=-1, x=1 ed è positiva per -1<x<0 e x>1

b) Le informazioni ottenute sono sufficienti per dare un grafico qualitativo (l'analisi della derivata seconda non permette di calcolare facilmente i due flessi sicuramente esistenti).

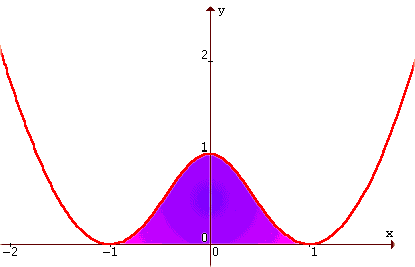
c) L'area della regione piana delimitata da k e dall'asse x è data da:

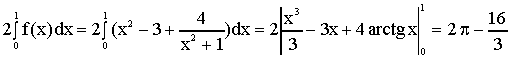
d) L'integrale richiesto corrisponde ad una regione piana che si ottiene da quella rappresentata dall'integrale precedente mediante l'affinità di equazioni: x=x'/3, y=y'; il rapporto tra le aree delle figure corrispondenti in tale affinità è 3; l'integrale in questione è quindi il triplo dell'integrale precedente.

Un altro modo per calcolare l'integrale è il seguente:

ponendo x/3 = t ovvero x = 3 t si ottiene dx=3dt; inoltre se x=0, t=0 e se x=3, t=1; quindi, integrando per sostituzione e sfruttando l'integrale già calcolato: