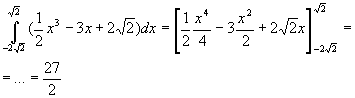y = ax3 + 3x + b
![]()
y'=3ax2+3=0
tale equazione ammette due soluzioni se e solo se a<0; quindi:
esistono massimo e minimo realtivo se e solo se a<0;
non esistono massimo e minimo realtivo se e solo se a>0.
MaturitÓ ordinaria 1998 - Soluzione quesito 1
a)
y = ax3 + 3x + b
![]()
y'=3ax2+3=0
tale equazione ammette due soluzioni se e solo se a<0; quindi:
esistono massimo e minimo realtivo se e solo se a<0;
non esistono massimo e minimo realtivo se e solo se a>0.
![]()
b)
Determiniamo a in modo che siano soddisfatte le condizioni richieste.
y'=0 quando
![]()
y"=6ax;
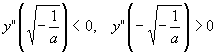
quindi nel primo caso c'Ŕ il massimo relativo e nel secondo il minimo relativo.
I valori di a e b si ottengono risolvendo il sistema
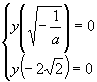
Ricavando b dalla prima equazione e sostituendo nella seconda si ottiene (razionalizzando) l'equazione
128a3+96a2+18a+1=0 (con a<-3/8)
che si abbassa di grado con a = - 1/2, mediante la regola di Ruffini:
(a+1/2)(128a2+32a+2)=0 per a= - 1/2 e a = - 1/8 (non accettabile).
La soluzione richiesta Ŕ quindi a = - 1/2.
Sostituendo nella prima equazione del sistema si ottiene
![]() .
.
La curva g richiesta ha quindi equazione
![]()
![]()
c)
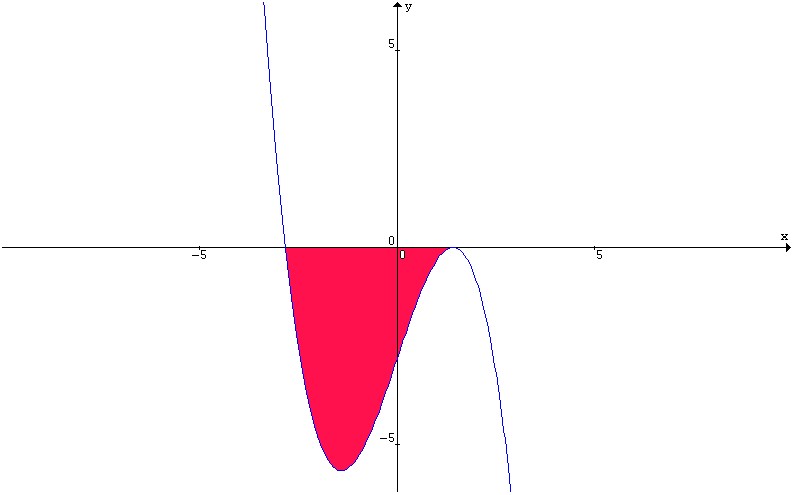
![]()
Tale curva ha i seguenti punti caratteristici:
![]()
ed il suo grafico Ŕ il seguente:
![]()
d)
L'area richiesta si ottiene calcolando il seguente integrale