Sessione ordinaria - Indirizzo d'ordinamento 1999
Soluzione quesito 1
a)
La condizione è necessaria ma non sufficiente. Si tratta del cosiddetto TEOREMA DI FERMAT, secondo cui:
Se x0 è un punto di massimo o minimo relativo per la funzione f(x) e in tale punto la funzione è derivabile risulta:
f ' (x0) = 0
Dimostrazione
Per definizione di derivata si può dire che
![]()
Supponiamo che f ' (x0) non sia nulla e sia, per esempio, f ' (x0) > 0.
In base al teorema della permanenza del segno esiste un intorno I di x0 in cui risulta
![]()
Ma allora in I risulta che:
e quindi x0 non può essere punto di massimo né di minimo.
In modo del tutto analogo si ragiona nel caso in cui sia f ' (x0) < 0.
N.B. Un'altra dimostrazione è quella che viene di solito presentata sui libri di testo nell'ambito della dimostrazione del teorema di Rolle.
Osservazioni
y = x3.

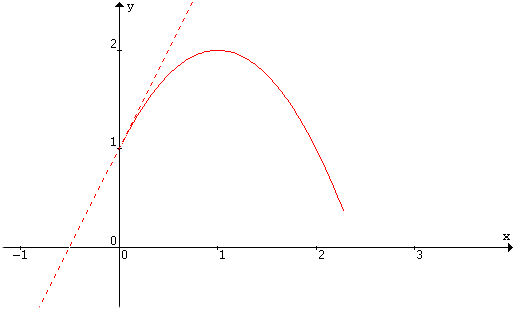
Nel punto (0;1) c'è chiaramente un minimo relativo senza che la derivata si annulli.
![]()
b)
![]()
Si calcola la derivata:
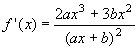
Per determinare i valori di a e b si deve risolvere il sistema
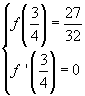
che conduce al sistema:
![]()
la cui soluzione è a = 2 e b = -1. La funzione richiesta ha quindi equazione:
![]()
![]()
c)
![]()
y ~ (1/2) x2
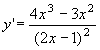 ; dallo studio della
derivata si scopre che il punto (0;0) è un flesso a tangente orizzontale e, come già
noto, che
; dallo studio della
derivata si scopre che il punto (0;0) è un flesso a tangente orizzontale e, come già
noto, che![]() è un
minimo relativo.
è un
minimo relativo.
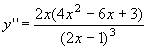 ; dallo studio della
derivata seconda si ritrova il flesso (0;0) e si scopre che la concavità del grafico è
verso l'alto per x<0 e per x>1/2, verso il basso per 0<x<1/2. Il grafico della
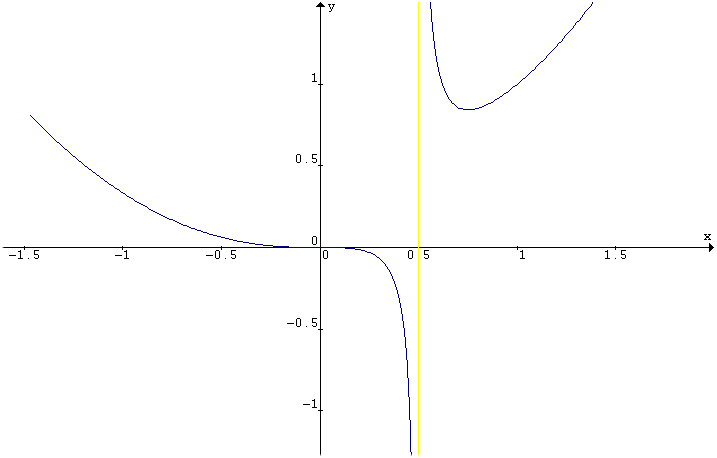
funzione è quindi il seguente:
; dallo studio della
derivata seconda si ritrova il flesso (0;0) e si scopre che la concavità del grafico è
verso l'alto per x<0 e per x>1/2, verso il basso per 0<x<1/2. Il grafico della
funzione è quindi il seguente:
![]()
d)
Il grafico della funzione di equazione y = f ' (x) può essere ricavato da quello già trovato tenendo presente che:
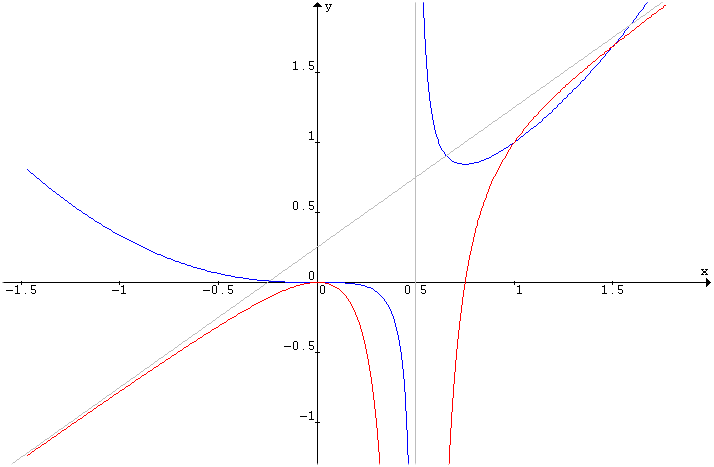
I due grafici si intersecano nei punti di coordinate (0;0), (1;1) e (3/2; 27/16).
![]()
e)
La relazione tra i due grafici è quella dettagliata nel punto
precedente.
![]()