Sessione ordinaria - Indirizzo d'ordinamento 1999
Soluzione quesito 2
a)

Per comoditÓ grafica si Ŕ posta l'unitÓ di misura uguale al raggio R della circonferenza.
Rispetto al sistema fissato la circonferenza k ha equazione
x2 + y2 = R2
![]()
b)
Indicato con V il vertice della parabola p, in base al Teorema di Archimede deve essere:
![]()
La parabola passa per A, B e per il punto V = (0;-2R). La generica parabola per A e B ha equazione del tipo:
y = a ( x - R ) ( x + R ) = a ( x2 - R2 )
ed imponendo il passaggio per V si ottiene a = 2/R; la parabola ha quindi equazione:
![]()
![]()
c)
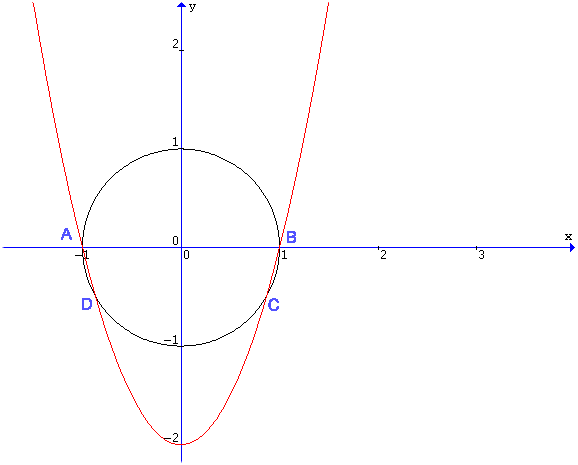
Per trovare i punti comuni alla circonferenza e alla parabola si deve risolvere il sistema
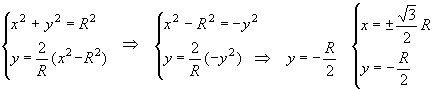
I punti comuni alle due curve sono quindi:
![]()
![]()
d)
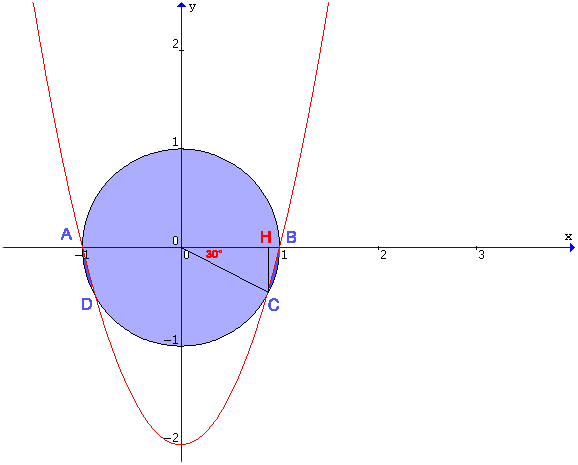
La parabola divide il cerchio in tre regioni, due delle quali hanno ugual area.
Calcoliamo l'area della regione del quarto quadrante delimitata dagli archi BC di parabola e di circonferenza; indicata con S tale area, si ha:
S = area settore circolare OBC- area triangolo OHC- area triangolo mistilineo HBC
individuato dalla parabola.
Essendo la misura del cateto HC metÓ del raggio OC si ha che l'angolo in O del
triangolo OHC misura 30░. Si ha pertanto:
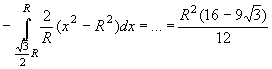
L'area S richiesta vale quindi:
![]()
Questo Ŕ anche il valore dell'area della regione del terzo quadrante delimitata dalle due curve.
La terza regione si ottiene sottraendo all'area del cerchio 2S; si ha quindi:
![]()
![]()
e)
Deve essere:
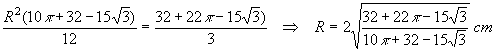
N.B.
Quasi certamente l'estensore del quesito voleva indicare il valore
![]()
che portava al semplice valore R=2.
![]()