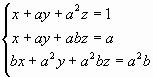
Seconda prova scritta
SESSIONE STRAORDINARIA
ESAME DI STATO DI LICEO SCIENTIFICO
a.s. 2001/2002CORSO SPERIMENTALE - PIANO NAZIONALE INFORMATICA
Tema di MATEMATICA
Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario.
PROBLEMA 1.
Considerato il seguente sistema lineare nelle incognite x, y, z:
[1] ; 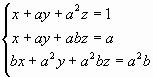
stabilire sotto quali condizioni per i parametri reali a, b esso è:
determinato;
indeterminato;
impossibile.
Posto che la terna (x,y,z) sia una soluzione del sistema [1], studiare la curva di equazione:
![]()
e disegnarne l’andamento in un riferimento cartesiano ortogonale (Oab).
PROBLEMA 2.
Con riferimento ad un sistema di assi cartesiani ortogonali (Oxy):
studiare le funzioni:
![]() ,
, ![]()
e disegnare i loro grafici;
dopo aver verificato che, oltre al punto O, tali grafici hanno in comune un altro punto A, determinare sul segmento OA un punto P tale che, condotta per esso la retta parallela all’asse y, sia massima la lunghezza del segmento RS, dove R ed S sono i punti in cui la retta interseca i due grafici suddetti;
determinare le coordinate dei punti di ascisse uguali in cui le due curve hanno tangenti parallele e verificare che, oltre al punto A, si ritrovano i punti R ed S;
calcolare il volume del solido generato dalla regione finita di piano delimitata dalle due curve quando ruota di un giro completo intorno all’asse x.
QUESTIONARIO.
In un piano è assegnata una parabola p. Tracciata la tangente t ad essa nel suo vertice, chiamati M ed N due punti di p simmetrici rispetto al suo asse e indicate con M’ ed N’ rispettivamente le proiezioni ortogonali di M ed N sulla retta t, determinare il rapporto fra l’area della regione piana delimitata dalla parabola e dalla retta MN e quella del rettangolo MNN’M’, fornendo una esauriente dimostrazione.
Si consideri un cono circolare retto ottenuto dalla rotazione di un triangolo isoscele intorno all’altezza propriamente detta. Sapendo che il perimetro del triangolo è costante, stabilire quale rapporto deve sussistere fra il lato del triangolo e la sua base affinché il cono abbia volume massimo.
In un riferimento monometrico di assi
cartesiani ortogonali (Oxy) è assegnata l’iperbole di equazione ![]() . Considerati su di essa i punti A e B di ascisse
rispettivamente a ed
. Considerati su di essa i punti A e B di ascisse
rispettivamente a ed ![]() , con a¹ 0, si traccino le tangenti
all’iperbole in A e B. Calcolare l’area della regione piana delimitata
dall’iperbole e dalle tangenti considerate.
, con a¹ 0, si traccino le tangenti
all’iperbole in A e B. Calcolare l’area della regione piana delimitata
dall’iperbole e dalle tangenti considerate.
Dopo aver definito il limite destro e il limite sinistro di una funzione in un punto, ricorrere a tali definizioni per verificare che risulta:
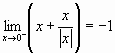 ,
, 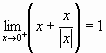 .
.
Considerata la funzione f(x) = ![]() , stabilire se è continua e derivabile nel punto x=2 e fornire
un’interpretazione geometrica delle conclusioni.
, stabilire se è continua e derivabile nel punto x=2 e fornire
un’interpretazione geometrica delle conclusioni.
Dimostrare la formula che esprime il numero delle combinazioni semplici di n oggetti presi a k a k in funzione del numero delle disposizioni semplici degli stessi oggetti presi a k a k e delle permutazioni semplici su k oggetti.
Un’urna contiene 100 palline numerate da 1 a 100. Determinare la probabilità che estraendo a caso una pallina, essa sia contrassegnata da un numero:
divisibile per 10 o per 8,
divisibile per 10 e per 8,
non divisibile per 10 né per 8.
Con riferimento ad un sistema di assi cartesiani ortogonali (Oxy), determinare le coordinate del baricentro del triangolo in cui l’omotetia di centro (1, 2) e caratteristica 1/4 trasforma il triangolo di vertici (4, 0), (-4, 4), (0, 8).
Tra le affinità di equazioni:
![]()
assegnate in un piano riferito ad un
sistema di assi cartesiani ortogonali (Oxy), determinare quella che trasforma i punti di
coordinate ![]() e
e 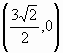 ordinatamente nei punti di coordinate
ordinatamente nei punti di coordinate 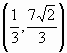 e
e 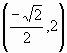 .
.
Scrivere un algoritmo che risolva il problema di determinare una radice approssimata di un’equazione con un’approssimazione voluta.
__________________________________________________________________________
Durata massima della prova: 6 ore.
È consentito soltanto l’uso di calcolatrici non programmabili.
Non è ammesso lasciare l’aula degli esami prima che siano trascorse tre ore dalla dettatura del tema.