Maturità sperimentale 1997- Soluzione quesito 3

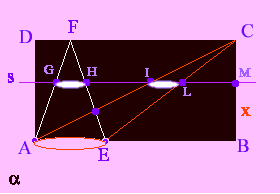
a) Dobbiamo dimostrare che i due segmenti GH e IL sono uguali.

I due triangoli AEF e GHF si corrispondono nell'omotetia di centro F e quindi il rapporto tra i lati GH ed AE è uguale al rapporto tra le relative altezze, che misurano rispettivamente (a-x) e a:

GH:AE=(a-x):a => GH=(a-x)2r/a ;

analogamente si corrispondono i triangoli ABC e IMC nell'omotetia di centro C, pertanto si ha:

IM:AB=CM:CB => IM=CM*AB/CB => IM=2(a-x).

Ma nella stessa omotetia si corrispondono anche i triangoli EBC ed LMC, pertanto:

LM:EB=CM:CB => LM=EB*CM/CB => LM=(2a-2r)(a-x)/a

Ma risulta:

IL=IM-LM=.........=(a-x)2r/a

come volevasi dimostrare.

b) C'₁ è una circonferenza perché corrispondente della circonferenza C₁ nell'omotetia solida di centro F; analogamente risulta C'₂ una circonferenza perchè corrispondente della circonferenza C₁ nell'omotetia solida di centro C. Da notare che le due omotetie hanno rapporto uno inverso dell'altro, pertanto la loro composizione è una traslazione: ciò conferma che le due sezioni sono isometriche.

c) I due coni hanno la stessa base e la stessa altezza quindi sono equivalenti; il loro volume è:

d)

Soluzione sintetica.

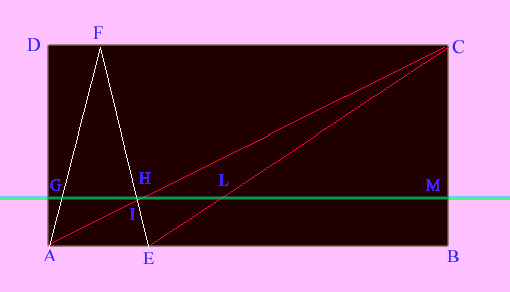
Osservando le due figure si nota che le due circonferenze sono tangenti esternamente quando I coincide con H, ovvero quando la misura del segmento IH è nulla. Pertanto:

HI=AB-r-GH/2-IM=2a-2(a-x)-r-r(a-x)/a=0;

da cui, con semplici calcoli:

Soluzione analitica.

Fissiamo un sistema di riferimento cartesiano ortogonale monometrico col centro in A, asse x coincidente con la retta AB (orientato da A verso B) e asse y coincidente con la retta AD (orientato da A verso D).

In tale riferimento risulta A=(0;0), F=(r;a), E=(2r;0), C=(2a;a);

equazione retta EF: (y-a)/a=(x-r)/(-r) => y=(-a/r)x+2a

equazione della retta AC: y=(1/2)x

Intersecando le due rette si trova il punto H, che risulta di coordinate

x=(4ar)/(r+2a)

y=(2ar)/r+2a)

L'ordinata di H fornisce il valore della distanza richiesta.