Maturità sperimentale 1998- Soluzione quesito 1
a)
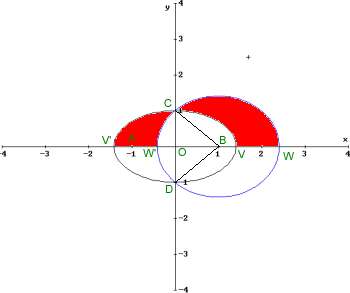
A(-1;0)
B(1;0)
G
1 è l'ellisse di fuochi A e B semiasse maggiore a=b2=a2-c2=1; pertanto l'ellisse ha equazione
x2/2+y2=1.
G2
è evidentemente la circonferenza di equazione(x-1)2+y2=2.

![]()
b)
C(0;1) e D(0;-1), vertici dell'ellisse, appartengono alla circonferenza poichè
![]()
quindi il triangolo CBD è retto in B.
(alla stessa conclusione si può giungere notando che gli angoli CBO e DBO misurano 45°).
![]()
c)
S
=area semiellisse+area semicerchio-2Area(W'CV)= area semiellisse +area semicerchio-(area semiellisse+Area segmento circolare CW'D)= area semicerchio-area segm. circ.= area semicerchio - (1/4 area cerchio- area triangolo CBD)= 1/4 area cerchio + Area tr. CBD== (p /2 +1) u2
![]()
d)
Notiamo che il punto P deve appartenere al segmento V'W, quindi
![]()
![]()
![]()
la sezione è un cerchio con R2=y2, essendo y l'ordinata di un punto dell'ellisse di ascissa x:
y2=1-x2/2
in tal caso risulta
f(x)=p (1-x2/2)
![]()
![]()
in tal caso la sezione è una corona circolare; risulta:
f(x)=p |R2-r2|=p |1-x2/2-(2-(x-1)2|=p |x2/2-2x|
![]()
![]()
in tal caso la sezione è un cerchio; risulta:
f(x)=p (2-(x-1)2=p (-x2+2x+1)
Il grafico di y=f(x) è quindi costituito da quattro archi di parabola:
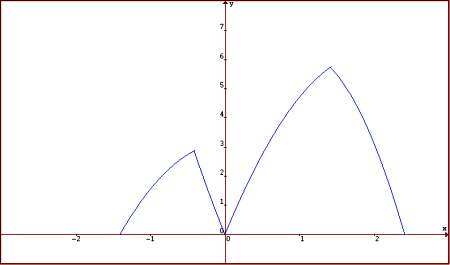
![]()
e)
Tenendo presente che f(x)dx=dV, essendo V il volume di T, evidentemente l'area in questione rappresenta il volume del solido T.