Sessione ordinaria - Indirizzo P.N.I. 1999
Soluzione quesito 1

 

 

 

a)

y' = x - 1

 

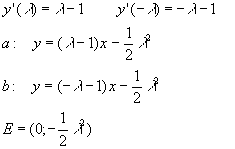
b)

 

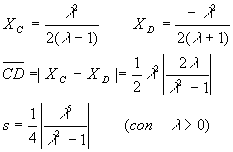
c)

E' sufficiente studiare la funzione di equazione

che ha come derivate prima e seconda

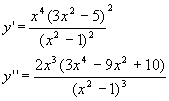
Si ottiene  il grafico

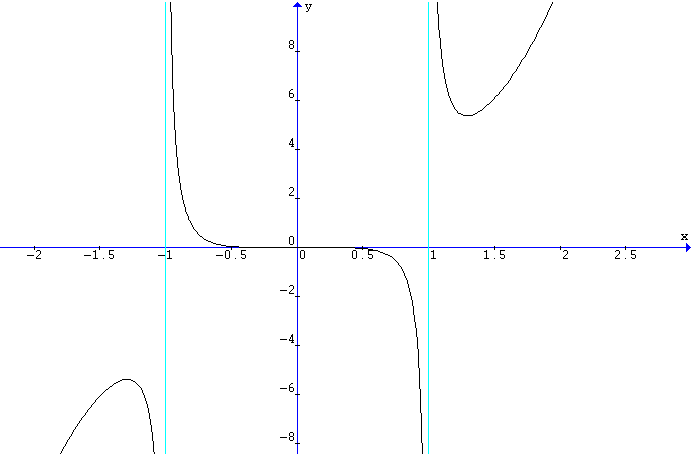
graf3.gif (5458 byte)

 

Da questo, tenendo conto delle limitazioni sulla x si ottiene il grafico richiesto

 

 

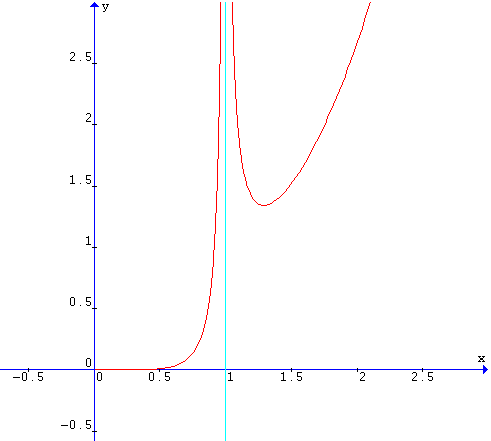
L'analisi della derivata prima permette di stabilire che il minimo relativo si ottiene per

 

d)

In corrispondenza del valore

si ottiene

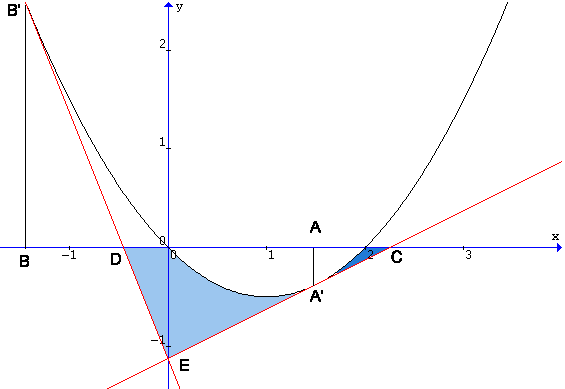
L'area richiesta (v. figura iniziale) si ottiene sommando l'area del triangolo OED e l'area del triangolo mistilineo OEA':

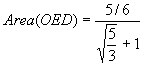
Per l'area di OEA' si deve calcolare l'integrale

 

 

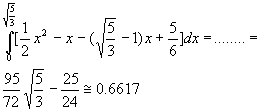
N.B.

Se si considera anche il triangolo mistilineo compreso tra l'asse x, la parabola ed il segmento A'C basta sottrarre allarea del triangolo ECD il segmento parabolico sotto l'asse delle x:

 

 

e)


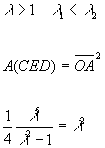
che, con le condizioni su l, conduce all'equazione di terzo grado

l3 - 4l2 + 4 = 0

Uno studio qualitativo della funzione di equazione

y = x3 - 4x2 + 4

porta al grafico

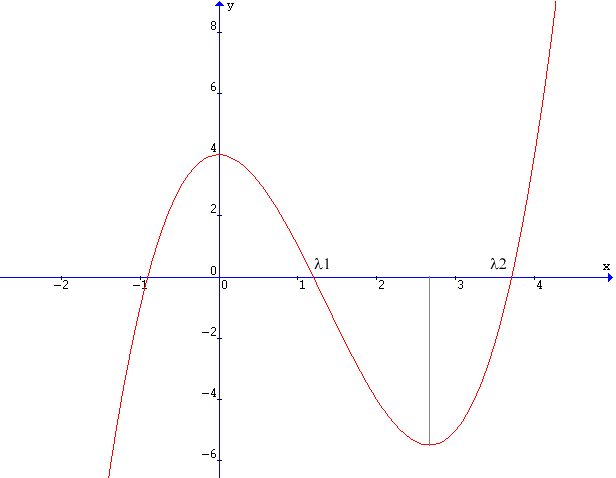
graf5.gif (4985 byte)

 

da cui si nota che la radice richiesta è compresa tra 1 e 2 ( Derive fornisce per le due radici positive i valori approssimati

1.19393 e 3.70927).

 

Un possibile programma in Pascal (che usa il metodo di bisezione ) per calcolare un valore approssimato della prima radice positiva è il seguente:

PROGRAM  pni99;

Uses Crt;

Const    a=1;
         b=2;

Var      n:integer;
         c:real;
         risposta:char;
(*------------------------------------------------------------------------*)

Procedure Presentazione;

Begin
  Writeln('Questo programma permette di calcolare la radice di ');
  writeln('X^3 - 4X^2 +4 = 0       nell''intervallo [1;2]');
  Writeln('a meno di 10 ^(-n) ');
  Writeln;writeln;

End;
(*------------------------------------------------------------------------*)

Procedure  Dati;
Begin
 Write('n = ');
 Readln(n);
 Writeln;
 Writeln('--------------------------------------------------')
End;
(*------------------------------------------------------------------------*)

Function  f(x:real):real;
Begin
  f:=x*x*x-4*x*x+4
End;

(*------------------------------------------------------------------------*)

Procedure  Elabora;

Var   errore,x1,x2:real;

Begin
  errore:=exp(-n*ln(10));   (*10^(-n)*)
  x1:=a;        x2:=b;
  Repeat
    c:=(x1+x2)/2;
    If f(c)*f(x1)<0 then
    x2:=c  ELSE   x1:=c
  Until  (abs(x2-x1)<errore)  or (f(c)=0)
end;

(*------------------------------------------------------------------------*)

Procedure Comunica;

 Begin
  Writeln('La radice , con l''approssimazione richiesta ‚ : ',c:10:n);
  Writeln;
  Writeln('--------------------------------------------------')
End;

(*------------------------------------------------------------------------*)

BEGIN (*main*)

Repeat
 Clrscr;
 Presentazione;
 Dati;
 Elabora;
 Comunica;
 Write('Ancora? (s/n)  ');
 Readln(risposta);
Until risposta in ['n','N']

END.