T1
rappresenta un'omotetia di centro O e rapporto 2Sessione ordinaria - Indirizzo P.N.I. 1999
Soluzione quesito 3
a)
T1
rappresenta un'omotetia di centro O e rapporto 2
T2
rappresenta una rotazione di 90° in senso antiorario intorno all'origine O
T3
rappresenta una traslazione di vettore (2;-1)
b)
La trasformazione T è la composizione delle tre trasformazioni date, ovvero
le cui equazioni si ottengono come segue:
La T ha quindi equazioni
c)
T rappresenta una similitudine diretta di rapporto k=2; il rapporto tra le aree delle figure corrispondenti è k2 = 4. Tale trasformazione è una particolare affinità che muta circonferenze in circonferenze; come tutte le affinità mantiene il parallelismo tra le rette; k rappresenta il rapporto tra i segmenti corrispondenti, che è, appunto, costante.
ponendo X=x e Y=y nelle equazioni della trasformazione si scopre, con semplici calcoli, il punto unito (4/5;3/5)
Data la retta generica di equazione
aX + bY + c = 0 (a e b non contemporaneamente nulli)
La sua corrispondente in T ha equazione
2b x -2a y +2a - b + c = 0
Le due rette coincidono se
a/2b = b/(-2a) = c/(2a - b +c)
La prima uguaglianza diventa
-2 a2 = 2 b2
che è verificata solo per a e b contemporaneamente nulli, situazione mai verificata.
Non ci sono quindi rette unite.
d)
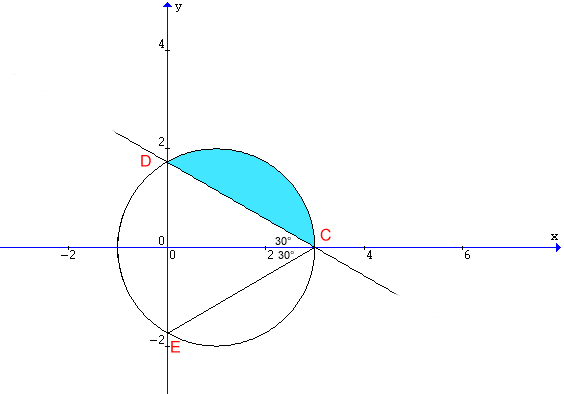
Risulta
pertanto l'angolo DCO misura 30°.
Il triangolo CDE è pertanto equilatero. Essendo
risulta R=2.
N.B. Il centro della circonferenza circoscritta ad un triangolo equilatero coincide con il baricentro, che nel nostro caso è il punto di coordinate (1;0); ma, per rispondere al quesito, non serve l'equazione della circonferenza.
Per determinare le aree ed i perimetri richiesti è sufficiente trovarli nella figura di partenza e poi applicare le proprietà della similitudine (l'area si moltiplica per 4 ed il perimetro per 2).
Detta A1 l'area del segmento circolare più piccolo risulta:
3 A1 = area cerchio - area triangolo CDE = 
quindi, indicata con A'1 la prima delle due aree richieste, si ha:
L'area del secondo segmento circolare si ottiene sottraendo all'area del cerchio l'area del primo segmento circolare:
e)
Il perimetro della prima regione è uguale ad un terzo della circonferenza più il lato del triangolo.
Con notazioni analoghe a quelle del punto precedente si ha:
Il perimetro della seconda regione è uguale a due terzi di circonferenza più il lato del triangolo:
N.B.
La circonferenza g ha centro (1;0) e raggio 2; la sua equazione è:
x2 + y2 - 2x -3 = 0
La circonferenza trasformata si ottiene applicando alla precedente la trasformazione T-1 le cui equazioni sono:
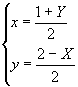
Si ottiene:
X2 + Y2 - 4X - 2Y -11 = 0
La retta a ha equazione
e la sua trasformata a'
