SOLUZIONISOLUZIONI

1

Si consideri il seguente sistema

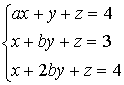
a) Discutere il sistema al variare dei parametri reali a e b.

b) Posto a = Y e b = X , tracciare il grafico della funzione Y = f(X) che si ottiene dalla relazione xo* yo = zo , dove xo, yo, zo rappresenta la soluzione del sistema nel caso in cui essa sia unica.

c) Trovare l’area S(k) della regione di piano insieme dei punti P(X,Y) tali che

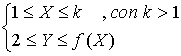
d) Determinare il limite di S(k) per k che tende a più infinito.

e) Produrre un programma in Pascal che permetta di calcolare la suddetta area.

a)

I determinanti della matrice A dei coefficienti, della matrice Ax che si ottiene sostituendo la prima colonna con la colonna dei termini noti, della matrice Ay che si ottiene sostituendo la seconda colonna con la colonna dei termini noti e della matrice Az che si ottiene sostituendo la terza colonna con la colonna dei termini noti risultano:

det A = b(1-a)

det Ax = 1-2b

det Ay = 1-a

det Az = -2ab+4b-1

Discussione:

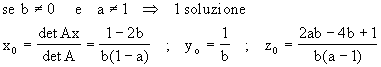
se a=1 risulta:

det Ax=1-2b

det Ay=0

det Az=2b-1

e quindi:

se b=1/2, il rango della matrice dei coefficienti ed il rango della matrice completa sono entrambi uguali a 2, quindi, in base al teorema di Rouchè-Capelli, il sistema ammette infinito alla uno soluzioni

Infine quando b=0, essendo det Ax=1 il sistema è impossibile (il rango della matrice completa è diverso del rango della matrice dei coefficienti).

Riepilogando si ha:

b)

Ponendo a=Y e b=X la relazione indicata fornisce la funzione di equazione

Se Y=1 si ottiene X=-1 e X=1/2, quindi l'isieme di definizione della funzione è dato da

Studio della funzione

• Se Y=0 si ha
  

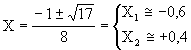
• limiti
  
  

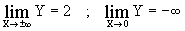
• derivata prima
  
  quindi si ha un massimo per X=2 ( con Y=17/8)

• derivata seconda
  
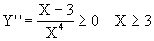
  quandi il grafico ha la concavità verso l'alto; il punto F=(3;19/9) è di flesso.

Il grafico della funzione è pertanto il seguente

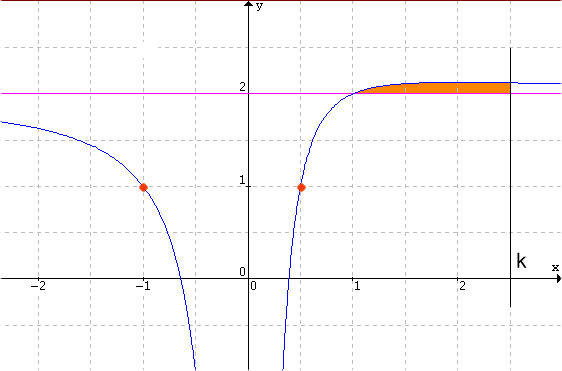
c)

L'area S(k) richiesta si ottiene mediante l'integrale

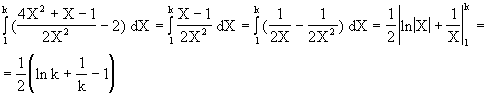
d)

Il limite richiesto è uguale a più infinito

e)

Program Compito;

Uses  Crt;

VAR
     n,h,i:integer;
     k,R,Dx,t:real;
     risposta:char;
(*------------------------------------------------------------------------*)
Procedure  Presentazione;
Begin
  ClrScr;
  Writeln('Questo programma permette di calcolare un integrale definito');
  writeln('mediante il metodo dei rettangoli.Il primo estremo ‚ fisso, il');
  Writeln('secondo, k, viene richiesto');
  Writeln;Writeln;

End;
(*------------------------------------------------------------------------*)

Procedure  Dati;
Begin
 Writeln('La funzione di cui si calcola l''integrale definito ‚: ');
 Writeln('                      y = (x-1)/(2*x*x) ');
 Repeat
  Writeln('Primo estremo = 1; inserisci il secondo estremo ( > 1 )');
  Write('k = ');
  Readln(k);
  Writeln('In quante parti vuoi dividere l''intervallo ? (n> 10 )');
  Write('n = ');
  Readln(n);

Until (k>1) and (n>10) and (int(n)=n);
 Writeln;
 Writeln('--------------------------------------------------')
End;
(*------------------------------------------------------------------------*)

Function  f(x:real):real;

Begin

f:=(x-1)/(2*x*x)

End;

 (*------------------------------------------------------------------------*)

Procedure    CalcolaR;

Begin
  h:=0;Dx:=(k-1)/n;
  R:=0;
  For i:=1 to n do
    begin
       t:=1+i*Dx;
       R:= R + Dx*f(t) ;
    end
  End;
 (*------------------------------------------------------------------------*)

Procedure Comunica;
Begin
  Writeln('numero divisioni n = ' , n);
  Writeln;
  Writeln('Integrale approssimato  = ',R:10:5);Writeln;
  Writeln;
  Writeln('Valore reale =  ',(1/2)*(ln(k)+1/k-1):10:5);
  Writeln('--------------------------------------------------');
  Writeln
End;

(*------------------------------------------------------------------------*)

BEGIN

Repeat
 Presentazione;
 Dati;
 CalcolaR;
 Comunica;
 Write('Ancora? (s/n)  ');
 Readln(risposta);
Until risposta in ['n','N']

END.