Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.


Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.
E' data la funzione \(y=f(x)=\frac{x+1}{x^2-4}\).
a) Trova il dominio
b) Stabilisci se è pari o dispari servendoti della definizione. Era possibile stabilire se era pari o dispari a partire dal dominio?
c) Trova le eventuali intersezioni con gli assi cartesiani.
d) Determina il segno della funzione.
e) Indica le regioni del piano in cui si trova il grafico della funzione e rappresenta graficamente tali regioni.
f) Dai un grafico probabile (qualitativo) della funzione.
Soluzione quesito 1:
Per trovare il dominio della funzione, dobbiamo escludere i valori di \(x\) per i quali il denominatore si annulla, poiché la divisione per zero non è definita.
Il denominatore è \(x^2-4\). Poniamo \(x^2-4 = 0\).
Risolvendo l'equazione: \(x^2 = 4\), da cui si ottiene \(x = \pm 2\).
Quindi, i valori da escludere sono \(x=2\) e \(x=-2\). Il dominio della funzione, che indichiamo con \(D\), è l'insieme di tutti i numeri reali tranne \(2\) e \(-2\).
Possiamo scrivere il dominio in notazione insiemistica come: \(D = \{x \in \mathbb{R} \mid x \ne \pm 2\}\).
Oppure in notazione per intervalli: \(D = (-\infty, -2) \cup (-2, 2) \cup (2, +\infty)\).
Per stabilire se la funzione è pari o dispari, dobbiamo verificare se valgono le seguenti condizioni:
Calcoliamo \(f(-x)\) sostituendo \(-x\) a \(x\) nella nostra funzione:
\[ f(-x) = \frac{(-x)+1}{(-x)^2-4} = \frac{-x+1}{x^2-4} \]Ora confrontiamo questo risultato con \(f(x)\) e \(-f(x)\).
Poiché la funzione non soddisfa nessuna delle due condizioni, non è né pari né dispari.
Poiché il dominio è simmetrico rispetto all'origine degli assi, non possiamo escludere che la funzione sia pari o dispari.
Per trovare le intersezioni con gli assi cartesiani, dobbiamo risolvere due sistemi:
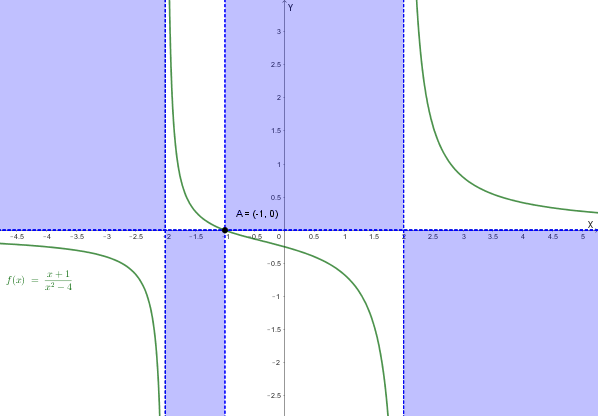
Poniamo \(x=0\) nella funzione: \(y = \frac{(0)+1}{(0)^2-4} = \frac{1}{-4} = -\frac{1}{4}\).
Il punto di intersezione con l'asse \(y\) è \( (0, -\frac{1}{4}) \).
Poniamo \(y=0\) e risolviamo l'equazione: \(\frac{x+1}{x^2-4} = 0\).
Una frazione è uguale a zero solo se il suo numeratore è uguale a zero, purché il denominatore non sia zero (cosa che abbiamo già gestito con il dominio).
Poniamo il numeratore uguale a zero: \(x+1 = 0\), da cui si ottiene \(x = -1\).
Il punto di intersezione con l'asse \(x\) è \( (-1, 0) \).
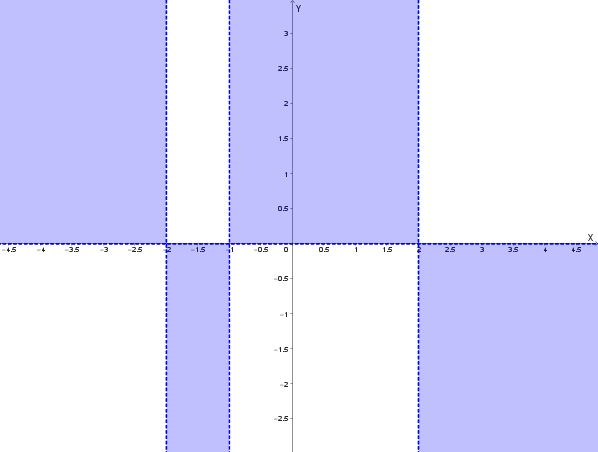
Per determinare il segno della funzione, dobbiamo studiare quando \(f(x) > 0\). Una frazione è positiva quando il numeratore e il denominatore hanno lo stesso segno.
Studiamo separatamente il segno del numeratore e del denominatore.
Poniamo \(x+1 > 0\), quindi \(x > -1\).
Poniamo \(x^2-4 > 0\), che è una disequazione di secondo grado.
Le radici dell'equazione associata \(x^2-4 = 0\) sono \(x = \pm 2\). Poiché il coefficiente di \(x^2\) è positivo (\(1 > 0\)), la disequazione è verificata per valori esterni alle radici.
Quindi, \(x^2-4 > 0\) per \(x < -2\) o \(x > 2\).
Ora, creiamo una tabella dei segni per la frazione \(f(x) = \frac{x+1}{x^2-4}\) tenendo conto dei valori \(-2\), \(-1\) e \(2\).
| Intervallo | \(x+1\) | \(x^2-4\) | \(f(x)\) |
|---|---|---|---|
| \(x < -2\) | - | + | - |
| \(-2 < x < -1\) | - | - | + |
| \(-1 < x < 2\) | + | - | - |
| \(x > 2\) | + | + | + |
In sintesi:
Dallo studio del segno, sappiamo che:
Le regioni in cui si trova il grafico sono le zone chiare del seguente grafico:
Un grafico qualitativo della funzione è il seguente:
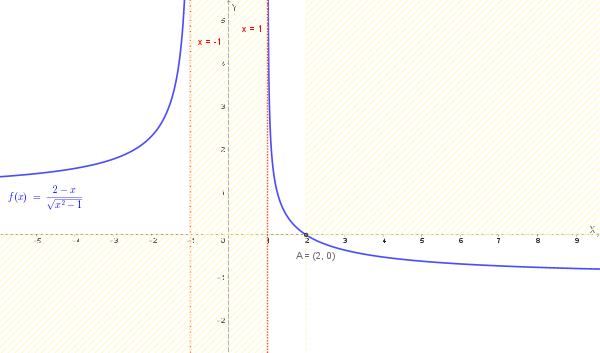
È data la funzione \(y=f(x)=\frac{2-x}{\sqrt{x^2-1}}\).
a) Trova il dominio
b) Stabilisci se è pari o dispari servendoti della definizione. Era possibile stabilire se era pari o dispari a partire dal dominio?
c) Trova le eventuali intersezioni con gli assi cartesiani.
d) Determina il segno della funzione.
e) Indica le regioni del piano in cui si trova il grafico della funzione e rappresenta graficamente tali regioni.
f) Dai un grafico probabile (qualitativo) della funzione.
Soluzione quesito 2:
Per trovare il dominio della funzione, dobbiamo assicurarci che il denominatore non sia nullo e che l'espressione sotto la radice quadrata sia strettamente positiva.
Il denominatore è \(\sqrt{x^2-1}\). Per essere definito, il radicando deve essere maggiore di zero, cioè \(x^2-1 > 0\).
Risolvendo la disequazione: \(x^2 > 1\), da cui si ottiene \(x < -1\) o \(x > 1\).
Quindi, il dominio della funzione, che indichiamo con \(D\), è l'insieme di tutti i numeri reali tali che \(x < -1\) o \(x > 1\).
Possiamo scrivere il dominio in notazione per intervalli: \(D = (-\infty, -1) \cup (1, +\infty)\).
Per stabilire se la funzione è pari o dispari, dobbiamo verificare se valgono le seguenti condizioni:
Calcoliamo \(f(-x)\) sostituendo \(-x\) a \(x\) nella nostra funzione:
\[ f(-x) = \frac{2-(-x)}{\sqrt{(-x)^2-1}} = \frac{2+x}{\sqrt{x^2-1}} \]Ora confrontiamo questo risultato con \(f(x)\) e \(-f(x)\).
Poiché la funzione non soddisfa nessuna delle due condizioni, non è né pari né dispari.
Poiché il dominio è simmetrico rispetto all'origine degli assi, non potevamo escludere a priori che la funzione fosse pari o dispari.
Per trovare le intersezioni con gli assi cartesiani, dobbiamo risolvere due sistemi:
Poniamo \(x=0\) nella funzione: il valore \(x=0\) non appartiene al dominio \(D = (-\infty, -1) \cup (1, +\infty)\). Pertanto, la funzione **non interseca l'asse \(y\)**.
Poniamo \(y=0\) e risolviamo l'equazione: \(\frac{2-x}{\sqrt{x^2-1}} = 0\).
Una frazione è uguale a zero solo se il suo numeratore è uguale a zero, purché il denominatore non sia zero. Poniamo il numeratore uguale a zero: \(2-x = 0\), da cui si ottiene \(x = 2\).
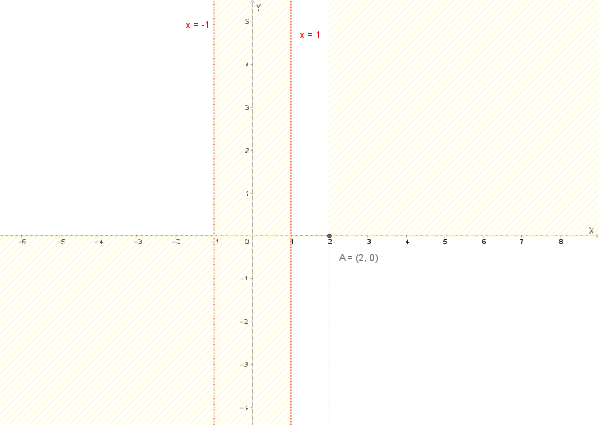
Il valore \(x=2\) appartiene al dominio della funzione (\(2 > 1\)). Quindi, il punto di intersezione con l'asse \(x\) è \( (2, 0) \).
Per determinare il segno della funzione, dobbiamo studiare quando \(f(x) > 0\). Una frazione è positiva quando il numeratore e il denominatore hanno lo stesso segno.
Studiamo separatamente il segno del numeratore e del denominatore.
Poniamo \(2-x > 0\), quindi \(-x > -2\), da cui si ottiene \(x < 2\).
La radice quadrata di un numero reale è sempre non negativa. Nel nostro dominio, l'argomento della radice è sempre positivo, quindi anche \(\sqrt{x^2-1}\) è sempre positivo.
Ora, creiamo una tabella dei segni per la frazione \(f(x) = \frac{2-x}{\sqrt{x^2-1}}\) tenendo conto del dominio e del valore \(x=2\).
| Intervallo | \(2-x\) | \(\sqrt{x^2-1}\) | \(f(x)\) |
|---|---|---|---|
| \(x < -1\) | + | + | + |
| \(-1 < x < 1\) | N.E. | N.E. | N.E. |
| \(1 < x < 2\) | + | + | + |
| \(x > 2\) | - | + | - |
In sintesi:
Dallo studio del segno, sappiamo che:
Di seguito un grafico per indicare le regioni del piano cartesiano in cui si trova la funzione. Le regioni tratteggiate sono le regioni in cui la funzione non esiste.
Un grafico qualitativo della funzione è il seguente:
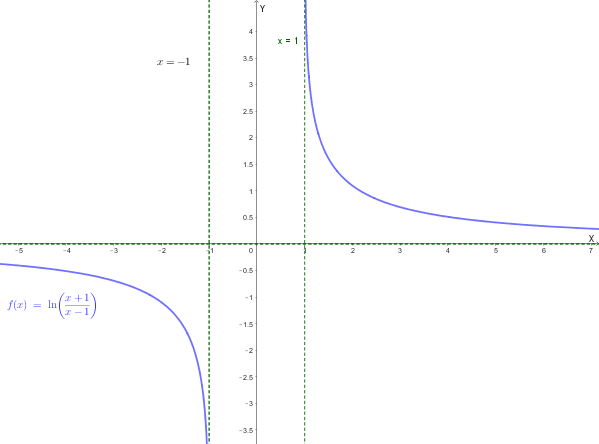
È data la funzione \(f(x) = \ln\left(\frac{x+1}{x-1}\right)\).
a) Trova il dominio
b) Stabilisci se è pari o dispari servendoti della definizione. Era possibile stabilire se era pari o dispari a partire dal dominio?
c) Trova le eventuali intersezioni con gli assi cartesiani.
d) Determina il segno della funzione.
e) Indica le regioni del piano in cui si trova il grafico della funzione e rappresenta graficamente tali regioni.
f) Dai un grafico probabile (qualitativo) della funzione.
Soluzione quesito 3:
Per trovare il dominio della funzione, dobbiamo assicurarci che l'argomento del logaritmo naturale sia strettamente positivo. Pertanto, dobbiamo risolvere la disequazione:
\[ \frac{x+1}{x-1} > 0 \]Studiamo il segno del numeratore e del denominatore separatamente:
Creiamo una tabella dei segni per la frazione:
| Intervallo | \(x+1\) | \(x-1\) | \(\frac{x+1}{x-1}\) |
|---|---|---|---|
| \(x < -1\) | - | - | + |
| \(-1 < x < 1\) | + | - | - |
| \(x > 1\) | + | + | + |
L'espressione \(\frac{x+1}{x-1}\) è positiva quando \(x < -1\) o \(x > 1\). Il dominio della funzione, che indichiamo con \(D\), è quindi l'insieme di tutti i numeri reali tali che \(x < -1\) o \(x > 1\).
Possiamo scrivere il dominio in notazione per intervalli: \(D = (-\infty, -1) \cup (1, +\infty)\).
Per stabilire se la funzione è pari o dispari, dobbiamo verificare se valgono le seguenti condizioni:
Calcoliamo \(f(-x)\) sostituendo \(-x\) a \(x\) nella nostra funzione:
\[ f(-x) = \ln\left(\frac{(-x)+1}{(-x)-1}\right) = \ln\left(\frac{1-x}{-x-1}\right) = \ln\left(\frac{-(x-1)}{-(x+1)}\right) = \ln\left(\frac{x-1}{x+1}\right) \]Ora confrontiamo questo risultato con \(f(x)\) e \(-f(x)\). Dalla proprietà dei logaritmi, \(\ln(a^{-1}) = -\ln(a)\). Possiamo scrivere il nostro risultato come:
\[ \ln\left(\frac{x-1}{x+1}\right) = \ln\left(\left(\frac{x+1}{x-1}\right)^{-1}\right) = -\ln\left(\frac{x+1}{x-1}\right) = -f(x) \]Poiché \(f(-x) = -f(x)\), la funzione è **dispari**.
Il dominio \(D = (-\infty, -1) \cup (1, +\infty)\) è simmetrico rispetto all'origine (se un numero \(x\) è nel dominio, anche il suo opposto \(-x\) lo è). Poiché il dominio è simmetrico rispetto all'origine, non era possibile escludere a priori se la funzione poteva essere pari o dispari.
Per trovare le intersezioni con gli assi cartesiani, dobbiamo risolvere due sistemi:
Poniamo \(x=0\). Poiché il valore \(x=0\) non appartiene al dominio \(D = (-\infty, -1) \cup (1, +\infty)\), la funzione **non interseca l'asse \(y\)**.
Poniamo \(y=0\) e risolviamo l'equazione: \(\ln\left(\frac{x+1}{x-1}\right) = 0\).
Per definizione di logaritmo, \(\ln(a) = 0\) se e solo se \(a=1\). Pertanto, dobbiamo risolvere l'equazione:
Moltiplichiamo entrambi i lati per \((x-1)\): \(x+1 = x-1\). Semplificando, otteniamo \(1 = -1\), che è una contraddizione. Questo significa che l'equazione non ha soluzioni.
Pertanto, la funzione **non interseca l'asse \(x\)**.
Per determinare il segno della funzione, dobbiamo studiare quando \(f(x) > 0\).
Poniamo \(\ln\left(\frac{x+1}{x-1}\right) > 0\).
Poiché la funzione logaritmo naturale è crescente, \(\ln(A) > \ln(1)\) se e solo se \(A > 1\). Quindi, dobbiamo risolvere la disequazione:
\[ \frac{x+1}{x-1} > 1 \]Portiamo \(1\) al lato sinistro e facciamo il denominatore comune:
\[ \frac{x+1}{x-1} - 1 > 0 \implies \frac{(x+1) - (x-1)}{x-1} > 0 \implies \frac{x+1-x+1}{x-1} > 0 \implies \frac{2}{x-1} > 0 \]Il numeratore è una costante positiva (2). Di conseguenza, la frazione è positiva se e solo se il denominatore è positivo.
\[ x-1 > 0 \implies x > 1 \]Ora consideriamo il dominio. L'espressione è definita solo per \(x < -1\) o \(x > 1\). Pertanto, il segno della funzione è:
Dallo studio del segno, sappiamo che:
Di seguito un grafico per indicare le regioni del piano cartesiano in cui si trova la funzione. Le regioni tratteggiate sono quelle in cui la funzione non esiste.

Un grafico qualitativo della funzione è il seguente:
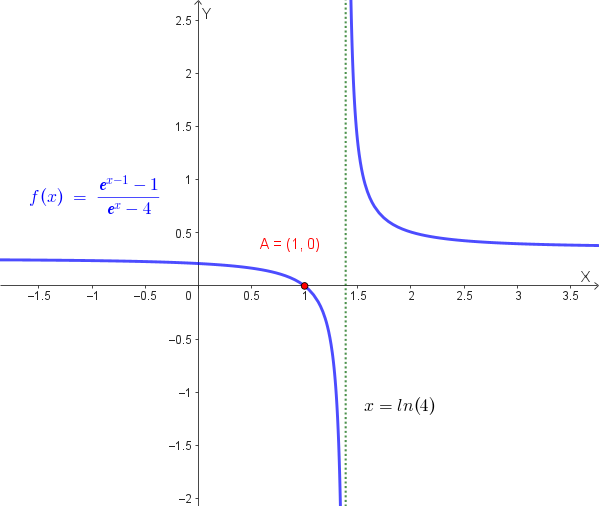
È data la funzione \(f(x) = \frac{e^{x-1} - 1}{e^x - 4}\).
a) Trova il dominio
b) Stabilisci se è pari o dispari servendoti della definizione. Era possibile stabilire se era pari o dispari a partire dal dominio?
c) Trova le eventuali intersezioni con gli assi cartesiani.
d) Determina il segno della funzione.
e) Indica le regioni del piano in cui si trova il grafico della funzione e rappresenta graficamente tali regioni.
f) Dai un grafico probabile (qualitativo) della funzione.
Soluzione quesito 4:
Per trovare il dominio della funzione, dobbiamo assicurarci che il denominatore non sia uguale a zero, poiché la divisione per zero non è definita.
Il denominatore è \(e^x - 4\). Poniamo \(e^x - 4 = 0\).
Risolviamo l'equazione: \(e^x = 4\).
Per trovare \(x\), applichiamo il logaritmo naturale a entrambi i lati: \(\ln(e^x) = \ln(4)\), da cui si ottiene \(x = \ln(4)\).
Quindi, l'unico valore da escludere è \(x = \ln(4)\).
Il dominio della funzione, che indichiamo con \(D\), è l'insieme di tutti i numeri reali tranne \(\ln(4)\).
Possiamo scrivere il dominio in notazione insiemistica come: \(D = \{x \in \mathbb{R} \mid x \ne \ln(4)\}\).
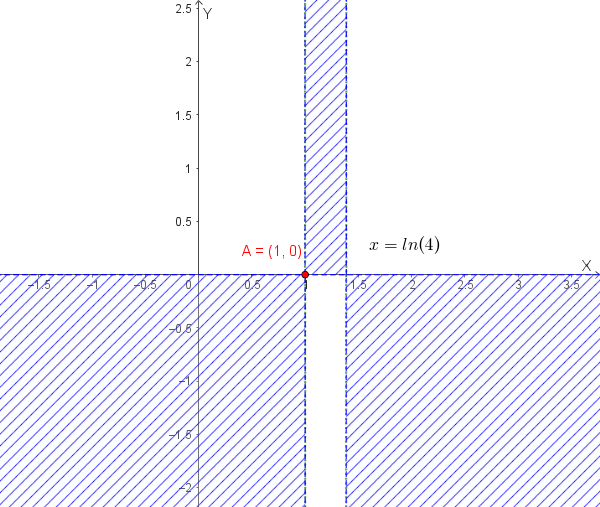
Oppure in notazione per intervalli: \(D = (-\infty, \ln(4)) \cup (\ln(4), +\infty)\).
Poiché il dominio non è simmetrico rispetto all'origine (se \(x\) è nel dominio, \(-x\) non necessariamente lo è, ad es. \(x = \ln(4)\) non è nel dominio, ma \(-x = -\ln(4) = \ln(1/4)\) lo è), la funzione non può essere né pari né dispari.
Per stabilire se la funzione è pari o dispari, la prima condizione da verificare è che il suo dominio sia simmetrico rispetto all'origine. Il dominio della nostra funzione è \(D = (-\infty, \ln(4)) \cup (\ln(4), +\infty)\). Questo dominio non è simmetrico, perché l'unico punto escluso è \(x = \ln(4)\), e il suo opposto \(x = -\ln(4)\) (che equivale a \(\ln(1/4)\)) non è un punto escluso.
Poiché il dominio non è simmetrico, la funzione non può essere né pari né dispari per definizione.
Per ulteriore chiarezza, possiamo calcolare \(f(-x)\) e confrontarlo con \(f(x)\) e \(-f(x)\):
\[ f(-x) = \frac{e^{(-x)-1} - 1}{e^{-x} - 4} = \frac{e^{-x-1} - 1}{e^{-x} - 4} = \frac{\frac{1}{e^{x+1}} - 1}{\frac{1}{e^x} - 4} = \frac{\frac{1-e^{x+1}}{e^{x+1}}}{\frac{1-4e^x}{e^x}} = \frac{1-e^{x+1}}{e^{x+1}} \cdot \frac{e^x}{1-4e^x} = \frac{e^x(1-e^{x+1})}{e^{x+1}(1-4e^x)} = \frac{1-e^{x+1}}{e(1-4e^x)} \]Dato che \(f(x) = \frac{e^{x-1} - 1}{e^x - 4}\), è evidente che \(f(-x) \ne f(x)\) e \(f(-x) \ne -f(x)\). Il calcolo conferma che la funzione non è né pari né dispari.
Per trovare le intersezioni con gli assi cartesiani, dobbiamo risolvere due sistemi:
Poniamo \(x=0\) nella funzione: \(y = \frac{e^{0-1} - 1}{e^0 - 4} = \frac{e^{-1} - 1}{1 - 4} = \frac{\frac{1}{e} - 1}{-3} = \frac{1-e}{-3e} = \frac{e-1}{3e}\).
Il punto di intersezione con l'asse \(y\) è \( \left(0, \frac{e-1}{3e}\right) \).
Poniamo \(y=0\) e risolviamo l'equazione: \(\frac{e^{x-1} - 1}{e^x - 4} = 0\).
Una frazione è uguale a zero solo se il suo numeratore è uguale a zero.
Poniamo il numeratore uguale a zero: \(e^{x-1} - 1 = 0\), da cui \(e^{x-1} = 1\).
Poiché \(e^0 = 1\), si deve avere \(x-1 = 0\), quindi \(x=1\).
Il valore \(x=1\) appartiene al dominio della funzione, poiché \(1 \ne \ln(4)\) (infatti \(\ln(4) \approx 1.386\)).
Il punto di intersezione con l'asse \(x\) è \( (1, 0) \).
Per determinare il segno della funzione, dobbiamo studiare quando \(f(x) > 0\). Una frazione è positiva quando numeratore e denominatore hanno lo stesso segno.
Studiamo separatamente il segno del numeratore e del denominatore.
Poniamo \(e^{x-1} - 1 > 0\), quindi \(e^{x-1} > 1\). Poiché \(1 = e^0\), si ha \(e^{x-1} > e^0\).
La funzione esponenziale \(e^x\) è strettamente crescente, quindi la disequazione è verificata quando gli esponenti hanno la stessa relazione d'ordine: \(x-1 > 0\), da cui \(x > 1\).
Poniamo \(e^x - 4 > 0\), quindi \(e^x > 4\).
Applicando il logaritmo naturale: \(x > \ln(4)\).
Ora, creiamo una tabella dei segni per la frazione \(f(x)\) tenendo conto dei valori \(1\) e \(\ln(4)\) (notiamo che \(\ln(4) > 1\)).
| Intervallo | \(e^{x-1}-1\) | \(e^x-4\) | \(f(x)\) |
|---|---|---|---|
| \(x < 1\) | - | - | + |
| \(1 < x < \ln(4)\) | + | - | - |
| \(x > \ln(4)\) | + | + | + |
In sintesi:
Dallo studio del segno, sappiamo che:
Di seguito un grafico per indicare le regioni del piano cartesiano in cui si trova la funzione. Le regioni tratteggiate sono le regioni in cui la funzione non esiste.
Un grafico qualitativo della funzione è il seguente:
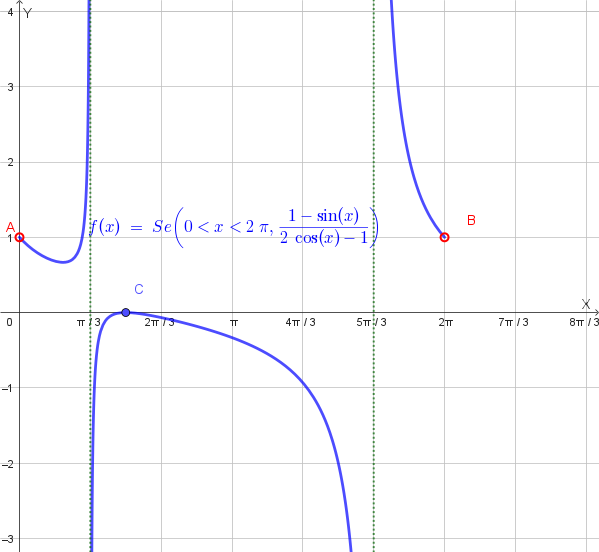
È data la funzione \(f(x) = \frac{1 - \sin(x)}{2\cos(x) - 1}\) nell'intervallo \([0, 2\pi]\).
a) Trova il dominio
b) Stabilisci se è pari o dispari servendoti della definizione. Era possibile stabilire se era pari o dispari a partire dal dominio?
c) Trova le eventuali intersezioni con gli assi cartesiani.
d) Determina il segno della funzione.
e) Indica le regioni del piano in cui si trova il grafico della funzione e rappresenta graficamente tali regioni.
f) Dai un grafico probabile (qualitativo) della funzione.
Soluzione quesito 5:
Per trovare il **dominio** della funzione nell'intervallo \([0, 2\pi]\), dobbiamo escludere i valori di \(x\) per i quali il denominatore si annulla. Il denominatore è \(2\cos(x) - 1\).
Poniamo \(2\cos(x) - 1 = 0\), da cui \(\cos(x) = \frac{1}{2}\). Nell'intervallo \([0, 2\pi]\), il coseno è uguale a \(1/2\) per due valori:
\[ x = \frac{\pi}{3} \quad \text{e} \quad x = \frac{5\pi}{3} \]Il dominio della funzione, \(D\), è l'intervallo dato, con l'esclusione di questi due punti. Possiamo scriverlo come: \(D = \left[0, \frac{\pi}{3}\right) \cup \left(\frac{\pi}{3}, \frac{5\pi}{3}\right) \cup \left(\frac{5\pi}{3}, 2\pi\right]\).
Per stabilire se la funzione è pari o dispari, è necessario che il suo dominio sia simmetrico rispetto all'origine. Poiché il nostro dominio \([0, 2\pi]\) non lo è, la funzione **non può essere né pari né dispari**.
Non è quindi necessario eseguire il calcolo di \(f(-x)\).
Per trovare le **intersezioni** con gli assi cartesiani, risolviamo due casi all'interno dell'intervallo \([0, 2\pi]\).
Poniamo \(x=0\) nella funzione: \(y = \frac{1 - \sin(0)}{2\cos(0) - 1} = \frac{1 - 0}{2(1) - 1} = \frac{1}{1} = 1\).
Il punto di intersezione con l'asse \(y\) è \( (0, 1) \).
Poniamo \(y=0\) e risolviamo l'equazione: \(\frac{1 - \sin(x)}{2\cos(x) - 1} = 0\). Una frazione è zero se il numeratore è zero e il denominatore non lo è. Poniamo il numeratore uguale a zero: \(1 - \sin(x) = 0\), da cui \(\sin(x) = 1\).
Nell'intervallo \([0, 2\pi]\), il seno è uguale a 1 solo per \(x = \frac{\pi}{2}\). A questo valore, il denominatore è \(2\cos(\frac{\pi}{2}) - 1 = 2(0) - 1 = -1 \ne 0\), quindi il punto è valido.
Il punto di intersezione con l'asse \(x\) è \( (\frac{\pi}{2}, 0) \).
Per determinare il **segno della funzione**, analizziamo separatamente il segno del numeratore e del denominatore nell'intervallo \([0, 2\pi]\).
Poiché \(-1 \le \sin(x) \le 1\), il numeratore \(1 - \sin(x)\) è sempre maggiore o uguale a zero. Si annulla solamente quando \(\sin(x) = 1\), cioè per \(x = \frac{\pi}{2}\).
Il denominatore è positivo quando \(2\cos(x) - 1 > 0 \implies \cos(x) > \frac{1}{2}\). Nell'intervallo \([0, 2\pi]\), questo si verifica per \(x \in \left[0, \frac{\pi}{3}\right) \cup \left(\frac{5\pi}{3}, 2\pi\right]\).
Il denominatore è negativo quando \(\cos(x) < \frac{1}{2}\), cioè per \(x \in \left(\frac{\pi}{3}, \frac{5\pi}{3}\right)\).
Combinando i segni del numeratore e del denominatore, possiamo costruire la seguente tabella:
| Intervallo | \(1 - \sin(x)\) | \(2\cos(x) - 1\) | \(f(x)\) |
|---|---|---|---|
| \([0, \frac{\pi}{3})\) | + | + | + |
| \(x = \frac{\pi}{2}\) | 0 | - | 0 |
| \((\frac{\pi}{3}, \frac{5\pi}{3})\) | + | - | - |
| \((\frac{5\pi}{3}, 2\pi]\) | + | + | + |
In sintesi, la funzione è **positiva** per \(x \in \left[0, \frac{\pi}{3}\right) \cup \left(\frac{5\pi}{3}, 2\pi\right]\), **negativa** per \(x \in \left(\frac{\pi}{3}, \frac{5\pi}{3}\right)\) e **uguale a zero** per \(x = \frac{\pi}{2}\).
Il grafico della funzione si trova **sopra l'asse \(x\)** negli intervalli \([0, \frac{\pi}{3})\) e \((\frac{5\pi}{3}, 2\pi]\). Si trova **sotto l'asse \(x\)** nell'intervallo \((\frac{\pi}{3}, \frac{5\pi}{3})\). Toccando l'asse \(x\) solo nel punto \(x=\frac{\pi}{2}\).
Di seguito un grafico per indicare le regioni del piano cartesiano in cui si trova la funzione. Le regioni tratteggiate sono le regioni in cui la funzione non esiste.

Un grafico qualitativo della funzione è il seguente.
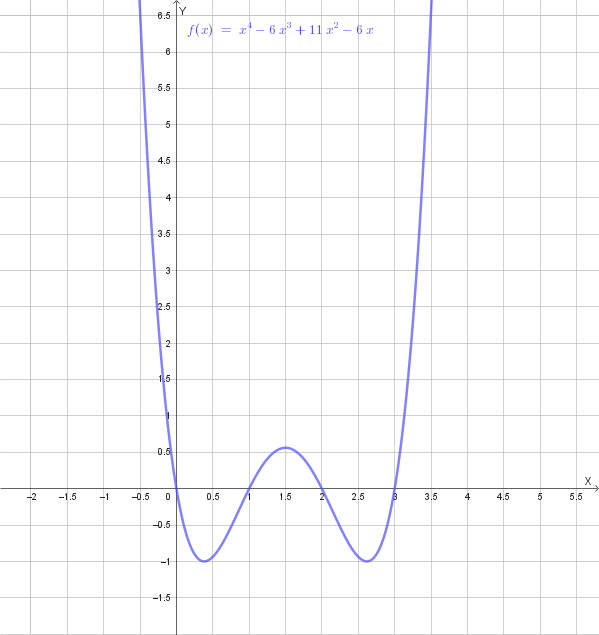
È data la funzione \(f(x) = x⁴ - 6x³ + 11x² - 6x\).
a) Trova il dominio
b) Stabilisci se è pari o dispari servendoti della definizione. Era possibile stabilire se era pari o dispari a partire dal dominio?
c) Trova le eventuali intersezioni con gli assi cartesiani.
d) Determina il segno della funzione.
e) Indica le regioni del piano in cui si trova il grafico della funzione e rappresenta graficamente tali regioni.
f) Dai un grafico probabile (qualitativo) della funzione.
Soluzione quesito 6:
Per trovare il **dominio** della funzione, consideriamo che \(f(x)\) è un polinomio. I polinomi sono definiti per qualsiasi numero reale, non avendo condizioni di esistenza da verificare (come denominatori, radici, ecc.).
Il dominio, \(D\), è l'insieme di tutti i numeri reali: \(D = \mathbb{R}\).
Per stabilire se la funzione è pari o dispari, verifichiamo la simmetria del dominio. Dato che il dominio è tutto \(\mathbb{R}\), la simmetria rispetto all'origine è verificata. Calcoliamo \(f(-x)\):
\[ f(-x) = (-x)⁴ - 6(-x)³ + 11(-x)² - 6(-x) = x⁴ + 6x³ + 11x² + 6x \]Confrontiamo \(f(-x)\) con \(f(x) = x⁴ - 6x³ + 11x² - 6x\). Poiché \(f(-x) \ne f(x)\) e \(f(-x) \ne -f(x)\), la funzione **non è né pari né dispari**.
Per trovare le **intersezioni** con gli assi cartesiani:
Poniamo \(x=0\): \(y = 0⁴ - 6(0)³ + 11(0)² - 6(0) = 0\).
Il punto di intersezione con l'asse \(y\) è \( (0, 0) \).
Risolviamo \(x⁴ - 6x³ + 11x² - 6x = 0\). Raccogliamo \(x\) a fattor comune:
Una radice è \(x=0\). Per il polinomio cubico, usiamo il Teorema di Ruffini. Provando con \(x=1\), troviamo che è una radice. Usando Ruffini, otteniamo \(x² - 5x + 6\). Le radici di questo polinomio si trovano risolvendo l'equazione di secondo grado:
Le altre radici sono \(x=3\) e \(x=2\).
Le intersezioni con l'asse \(x\) sono nei punti \( (0, 0) \), \( (1, 0) \), \( (2, 0) \) e \( (3, 0) \).
Per determinare il **segno della funzione**, studiamo quando \(f(x) > 0\). La forma fattorizzata è \(f(x) = x(x-1)(x-2)(x-3)\). Studiamo il segno di ogni fattore.
| Intervallo | \(x\) | \(x-1\) | \(x-2\) | \(x-3\) | \(f(x)\) |
|---|---|---|---|---|---|
| \(x < 0\) | - | - | - | - | + |
| \(0 < x < 1\) | + | - | - | - | - |
| \(1 < x < 2\) | + | + | - | - | + |
| \(2 < x < 3\) | + | + | + | - | - |
| \(x > 3\) | + | + | + | + | + |
In sintesi, la funzione è positiva per \(x < 0\), per \(1 < x < 2\) e per \(x > 3\). È negativa per \(0 < x < 1\) e per \(2 < x < 3\).
Dallo studio del segno, il grafico si trova **sopra l'asse \(x\)** negli intervalli \((-\infty, 0)\), \((1, 2)\) e \((3, +\infty)\). Si trova **sotto l'asse \(x\)** negli intervalli \((0, 1)\) e \((2, 3)\).
Di seguito un grafico per indicare le regioni del piano cartesiano in cui si trova la funzione. Le regioni tratteggiate sono le regioni in cui la funzione non esiste.

Un grafico qualitativo della funzione è il seguente.