Risolvi da solo i singoli problemi e controlla la soluzione premendo il tasto corrispondente.
Problema 1
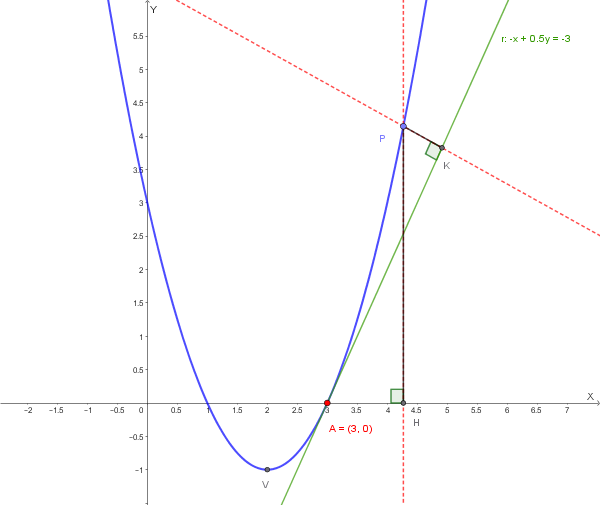
Data la parabola \( \mathcal{P} \) di equazione \( y = x^2 - 4x + 3 \). Sia \( V \) il vertice della parabola e sia \( P \) un punto generico della parabola situato nel primo quadrante, di coordinate \( P(x, y) \), con \( x > 3 \).
Detta \( r \) la **tangente** alla parabola nel suo punto \( A \) di ascissa \( x_A = 3 \), ed indicati con \( H \) e \( K \) le proiezioni di \( P \) rispettivamente sull'asse \( x \) e sulla retta \( r \), calcolare il seguente limite:
\[ L = \lim_{P \to A} \frac{PH}{PK} \]Problema 2
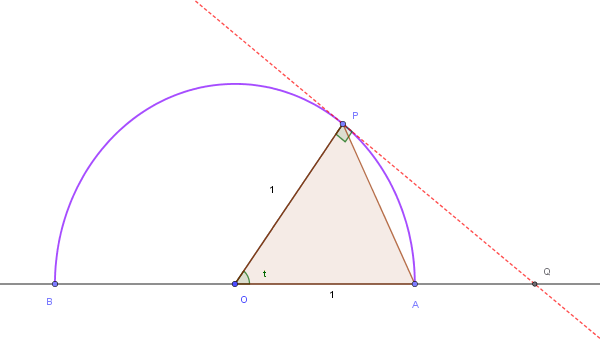
Nel piano, sia data una semicirconferenza di centro \( O \), raggio \( r = 1 \) e diametro orizzontale \( AB \) , con \( A \) a destra di \( O \).
Sia \( P \) un punto generico della semicirconferenza.
Indicato con \( t \) l'angolo al centro \( P\hat{O}A \), espresso in radianti (\( 0 < t < \pi \)), e detto \( Q \) il punto di intersezione tra la retta **tangente** alla semicirconferenza in \( P \) e la retta del diametro \( AB \), calcolare il seguente limite al tendere del punto \( P \) al punto \( A \):
\[ L = \lim_{P \to A} \frac{\overline{PQ}^2}{\text{Area del triangolo } (POA)} \]Problema 3
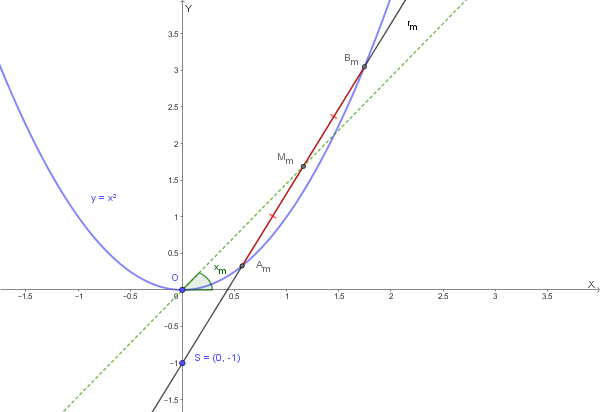
Nel piano cartesiano sia data la parabola
e la retta \(r_m\) che dipende da un parametro reale \(m>0\), definita da
La retta \(r_m\) intersechi la parabola in due punti distinti \(A_m\) e \(B_m\).
Sia \(M_m\) il punto medio del segmento \(A_mB_m\) e \(O(0,0)\) l'origine.
Si chiede di:
- Trovare le coordinate di \(M_m\) in funzione di \(m\).
- Determinare l'equazione della retta \(OM_m\).
- Indicato con \(x_m\) l'angolo acuto formato da \(OM_m\) con l'asse \(x\), calcolare il limite della quantità \(\frac{\tan x_m}{m}\) quando la retta secante \(A_m B_m\) **tende a diventare tangente** alla parabola.
Problema 4
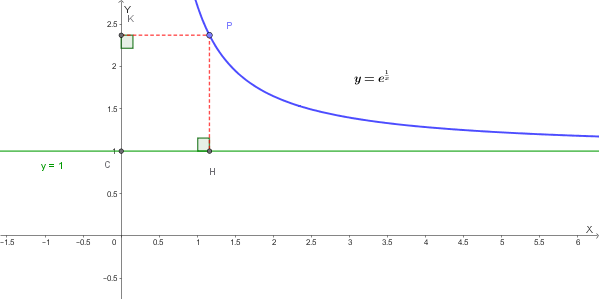
Si consideri la funzione di equazione \( y = f(x) = e^{\frac{1}{x}} \).
a) Si tracci un grafico qualitativo per \( x > 0 \) (dominio, intersezioni con gli assi, pari/dispari, segno, eventuali asintoti), **dopo aver dimostrato, servendosi della definizione, che per \( x>0 \) la funzione è strettamente decrescente**.
b) Sia \( P \) un generico punto appartenente al grafico della funzione e si indichino con \( H \) e \( K \) le proiezioni, rispettivamente, sull'asintoto orizzontale e sull'asse \( y \).
c) Indicata con \( t \) l'ascissa di \( P \), si calcoli il seguente limite:
\[ L = \lim_{t \to +\infty} (\overline{PH} \cdot \overline{PK}) \]Problema 5 (Maturità Scientifica 1992)
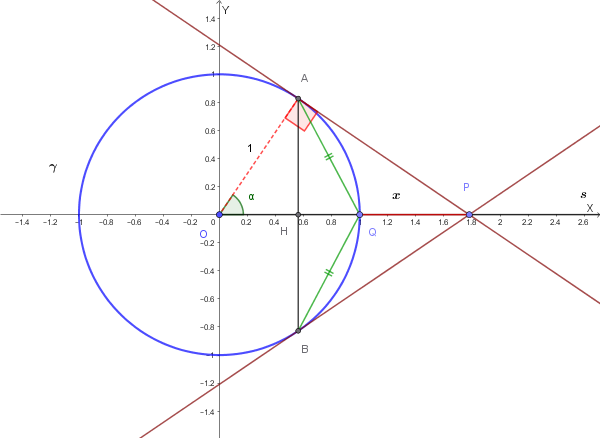
Data una **circonferenza \(\gamma\) di raggio unitario e centro \(O\)**, tracciare una semiretta \(s\) uscente da \(O\) ed intersecante \(\gamma\) in un punto \(Q\).
Indicato con \(P\) un generico punto di \(s\) **esterno alla circonferenza** \(\gamma\), tracciare da esso le due tangenti alla circonferenza: siano \(A\) e \(B\) i punti di tangenza.
Indicata con **\(x\) la lunghezza del segmento \(PQ\)**, si chiede di calcolare il seguente limite per \(x\) tendente ad infinito del rapporto:
\[ L = \lim_{x \to +\infty} \frac{\overline{AQ} + \overline{QB}}{\overline{AB}} \]Problema 6 (Maturità Scientifica 1992 - Sessione Suppletiva)
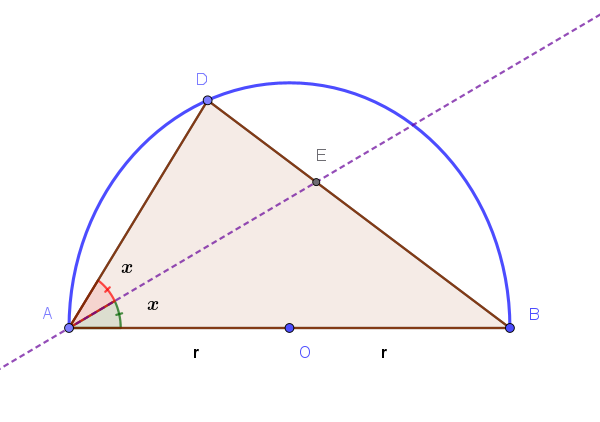
In una **semicirconferenza di diametro \(\overline{AB} = 2r\)** inscrivere il **triangolo \(\text{ABD}\) rettangolo in \(D\)**. Tracciare la bisettrice dell'angolo \(\text{DAB}\): tale bisettrice intersechi il segmento \(\overline{BD}\) in \(E\).
Indicato con \(x\) l'angolo \(\text{BAE}\), determinare il rapporto \(y\) tra la lunghezza del segmento \(\overline{BE}\) e la lunghezza del segmento \(\overline{BD}\):
\[ y = \frac{\overline{BE}}{\overline{BD}} \]Calcolare il rapporto \(y\) per \(x\) tendente a zero.
Problema 7
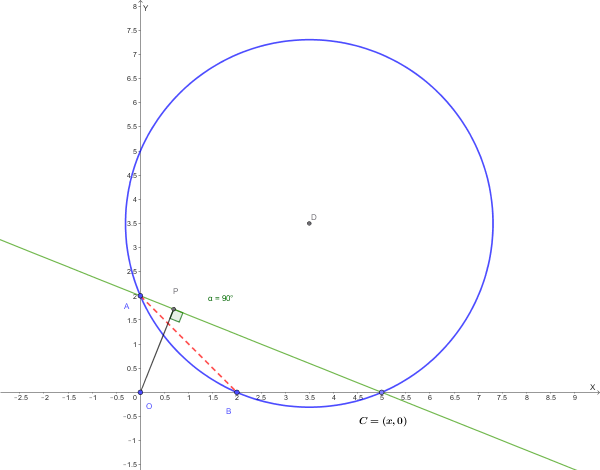
È assegnato, in un piano \(\alpha\), un sistema di assi cartesiani ortogonali (\(Oxy\)).
Si considerino i punti \(A(0, 2)\), \(B(2, 0)\), \(C(x, 0)\), con \(x > 2\).
Detta \(P\) la proiezione di \(O\) sulla retta \(AC\), **calcolare:**
\[ L = \lim_{x \to +\infty} \frac{\overline{OP}}{\overline{AB}} \]Quale luogo descrive il centro della circonferenza al variare di C?
Problema 8
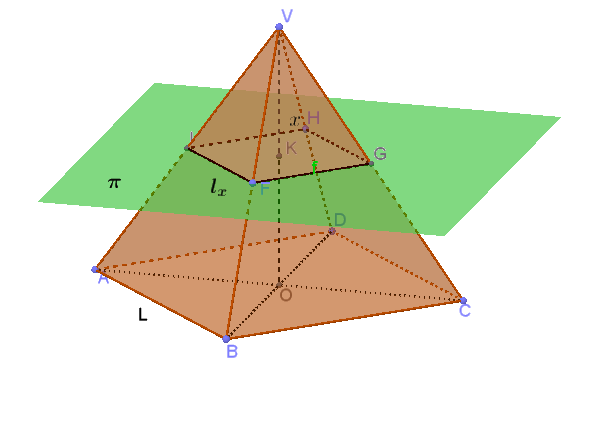
Si consideri una piramide retta a base quadrata di lato \(L=2\) e altezza \(H=4\).
Un piano \(\pi\) parallelo alla base seziona la piramide in due solidi. Sia \( x \) la distanza del piano \(\pi\) dal vertice.
Sia \( A_{sup}(x) \) l'area della sezione quadrata prodotta dal piano \(\pi\).
- Esprimi l'area \( A_{sup}(x) \) in funzione di \( x \).
- Determina l'espressione del rapporto \(\mathbf{k(x)}\) tra la variazione dell'area di base (\(A_{base} - A_{sup}(x)\)) e la distanza \( d \) del piano dalla base. \[ \mathbf{k(x) = \frac{A_{base} - A_{sup}(x)}{d}} \]
- Calcola il limite del rapporto \(\mathbf{k(x)}\) quando la sezione si avvicina alla base della piramide.