Riconoscimento di una conica
Esaminiamo dapprima il problema del riconoscimento di una conica degenere e della ricerca delle rette componenti. Il problema, come già accennato, consiste nello stabilire se il polinomio che individua la conica si può scomporre; nei casi più semplici la scomposizione è immediata. Vediamo come si può procedere in generale, prendendo spunto da un esempio.
2x2 - xy - y2 + 3x + 3y - 2 = 0
Ordiniamo l'equazione per esempio nella variabile y:
y2 + (x - 3) y - 2x2 - 3x + 2 = 0
Il discriminante di tale equazione è un quadrato perfetto quindi si può esprimere la y linearmente rispetto alla x e pertanto la conica si spezza in due rette; dopo semplici calcoli si ottiene:
(y + 2x - 1) (y - x - 1) = 0
In generale se almeno una delle variabili è di secondo grado si procede come nell'esempio precedente: la conica sarà degenere se il discriminante dell'equazione relativa è un quadrato perfetto. Se nessuna delle due variabili è di secondo grado avremo un'equazione del tipo:
axy + bx + cy + d = 0 (con a diverso da zero). Si presentano le seguenti possibilità:
x (ay+b) + (cy + d) = 0;
il primo membro sarà scomponibile se
ay + b = k(cy + d), con k non nullo; come dire:
a = kc, b = kd
ovvero
a/c = b/d , ad - bc = 0.
Esempi:
2xy = 0, xy + x = 0 , xy +3y = 0, xy + x + y +1 = 0.
Prima di esporre il procedimento per riconoscere una conica non degenere si porga l'attenzione alle possibili intersezioni con una generica retta parallela ad uno degli assi cartesiani:
un'ellisse, comunque disposta nel piano, ha due intersezioni con una generica retta x=h, per h'£h£h''; lo stesso dicasi per una generica retta del tipo y=k, per k'£k£k''.
2. Un'iperbole equilatera con gli asintoti paralleli agli assi cartesiani ha un'intersezione con ogni retta parallela ad uno degli assi cartesiani (escluse le rette che individuano gli asintoti).
3. Un'iperbole diversa da quelle esaminate nel punto precedente ha due intersezioni con una retta del tipo x=h oppure y=k in una zona del piano esterna ad una striscia ( ovvero per h£h', h³h'', k£k', k³k'').
4. Una parabola, comunque disposta, ha due intersezioni con una retta del tipo x=h oppure y=k in un semipiano (cioè per h£h' oppure h³h''; per k£k' oppure k³k'').
Detto questo è facile intuire come lo studio delle intersezioni con una generica retta parallela ad uno degli assi cartesiani permetta di riconoscere in maniera inequivocabile il tipo di conica.
Vediamo alcuni esempi:
2x2 + xy - y2 +3x - y = 0
Il discriminante dell'equazione ordinata rispetto alla x risulta
9y2 + 14y + 9
che non è un quadrato perfetto (quindi la conica non è degenere); risulta:
9y2 + 14y + 9 ³ 0
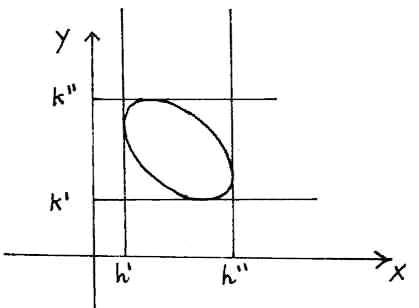
per ogni valore di y: ciò vuol dire che una qualsiasi retta y = k interseca la conica in due punti reali e distinti: non potremo avere né un'ellisse né una parabola; la conica é pertanto un'iperbole.
Notiamo che se ordiniamo l'equazione rispetto alla y ci accorgiamo che una generica retta del tipo x = h interseca la conica in due punti reali per
h £ -1 oppure per h ³ -1/9
2) x2 - 4xy + 4y2 + 4y = 0
Il discriminante dell'equazione ordinata rispetto alla x é -4y, che non é un quadrato perfetto e quindi la conica non é degenere; essendo
-4y ³ 0 per y £ 0
possiamo dire che la conica ha punti reali in un semipiano e, in base a quanto osservato precedentemente, non può che essere una parabola.
3) x2 - xy + y2 + x - y = 0
Il discriminante dell'equazione ordinata rispetto alla x é
-3y2 + 2y + 1
che non è un quadrato perfetto (la conica é irriducibile) ed é
-3y2 + 2y + 1 ³ 0 per -1/3 £ y £ 1
Questo basta per dire che la conica é un'ellisse (che é l'unica conica non degenere che può avere punti reali solo in una striscia).
Un analogo studio delle intersezioni con una generica retta parallela all'asse delle y porta alla conclusione che la conica ha punti reali in un quadrato con i lati paralleli agli assi cartesiani (-1 £ x £ 1/3).
Osservazione
Oltre al modo visto negli esempi precedenti si può ricorrere alle particolari simmetrie possedute dalle coniche reali non degeneri per riconoscerne il tipo. E' noto infatti che l'ellisse e l'iperbole possiedono un centro di simmetria e due assi (ortogonali) di simmetria (sono dette per questo coniche a centro); la parabola ha invece un solo asse di simmetria (ortogonale).
Una conica del tipo Ax2 + Bxy + Cy2 + D = 0
essendo simmetrica rispetto agli assi cartesiani (scambiando x in -x e y in -y l'equazione non cambia) non può essere una parabola.
In generale si può procedere in questo modo:
si esegue una traslazione degli assi cartesiani che porti l'origine nell'eventuale centro di simmetria C=(a;b):
x = X + a, y = Y + bsi impone che la nuova equazione manchi dei termini di primo grado in X e Y; se ciò é possibile avremo una conica a centro, altrimenti una parabola.
N.B. Quanto detto sopra permette di trovare l'eventuale centro di una conica.
IL TEOREMA SUL RICONOSCIMENTO DI UNA CONICA.
La conica di equazione
ax2 + bxy + cy2 + dx + ey + f = 0
é una parabola (eventualmente degenere in due rette parallele) se:
b2 - 4ac = 0
é un'ellisse (eventualmente immaginaria oppure degenere in un punto) se:
b2 - 4ac < 0
é una'iperbole (eventualmente degenere in due rette incidenti) se:
b2 - 4ac > 0.
DIMOSTRAZIONE
Ordinando l'equazione rispetto alla x si ottiene il discriminante
(b2 - 4ac) y2 + (2bd - 4ae) y + d2 - 4af
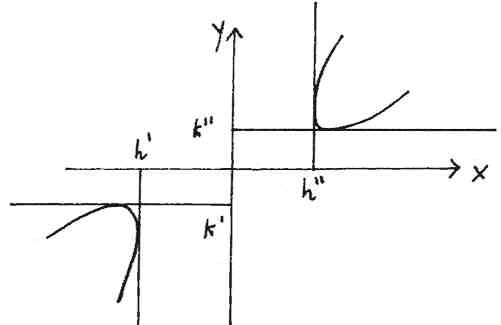
Se b2 - 4ac = 0 avremo punti reali in un semipiano: la conica in tal caso é una parabola; se é anche 2bd - 4ae = 0 avremo una conica degenere in due rette parallele, immaginarie se d2 - 4af < 0.
Se b2 - 4ac < 0 il suddetto discriminante é ³ 0 per valori interni (ed in tal caso la conica ha punti reali in una striscia e pertanto é un'ellisse) oppure é sempre negativo o nullo ed in tal caso é una conica completamente immaginaria oppure degenere in punto.
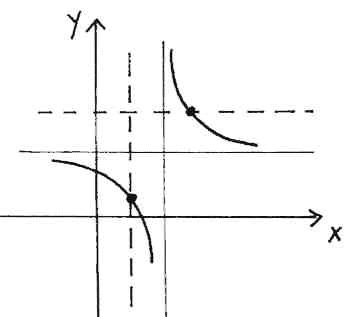
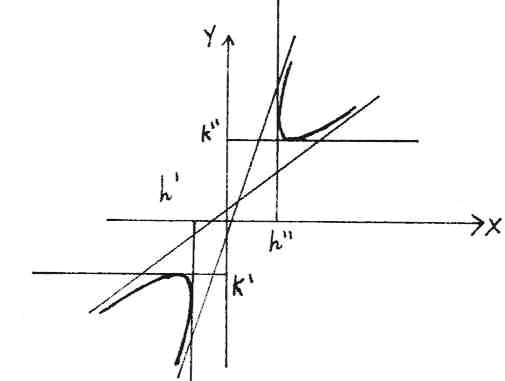
- Con un ragionamento analogo si scopre che quando
b2 - 4ac > 0 si ha un'iperbole o una conica degenere in due rette incidenti.
OSSERVAZIONE
La dimostrazione precedente permette di affermare che una conica é una parabola (eventualmente degenere in due rette parallele) se e solo se il complesso dei termini di secondo grado é un quadrato perfetto; una parabola ha quindi equazione del tipo
(ax + by)2 + cx + dy + e = 0
Si dimostra anzi che la retta di equazione ax + by = 0 é parallela all'asse della parabola.
