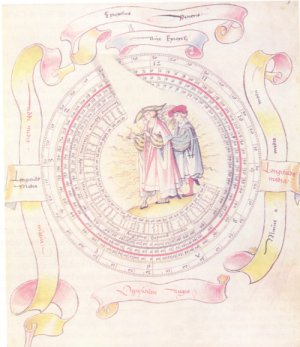
Schema semplificato del modello di Eudosso per descrivere il moto di un pianeta. La sfera esterna è quella delle stelle fisse, le tre sfere interne sono collegate ciascuna a quella immediatamente più esterna attraverso assi di rotazione opportunamente inclinati. Il pianeta si trova sulla sfera più interna. La Terra è posta al centro dell’Universo.

Schema tolemaico che mostra i deferenti e gli epicicli dei pianeti del sistema solare. Nel disegno a compaiono i pianeti posti tra la Terra e il Sole, nel disegno b i pianeti più lontani. Si noti che i raggi dei deferenti e degli epicicli sono scelti in modo che non vi siano sovrapposizioni nelle orbite, ma neppure spazi vuoti fra un epiciclo e l’altro.

 

 

 

 

 

 

 

 

 

Riproduzione del modello per l’Epiciclo di Venere di Sebastian Munster (1488-1552). Con aux Epicycli e Oppositum augis sono indicati il punto dell’orbita di Venere più vicino e il punto più lontano rispetto alla Terra. Ruotando opportunamente il disco interno rispetto a quello esterno si poteva individuare la posizione di Venere sull’epiciclo corrispondente a una prefissata data.
L’illustrazione al centro della figura ricorda che il destino astrologico dei nati sotto il segno di Venere era quello di svolgere attività mercantili portatrici di ricchezze.
Questa fusione di contenuti astronomici e astrologici sta a testimoniare la storicità delle teorie scientifiche, in qualche misura sempre radicate nella cultura e nella storia dell’epoca in cui vengono prodotte.

I MODELLI GEOCENTRICI

Il moto dei pianeti poneva in crisi l’ipotesi del moto circolare dei corpi celesti, e con ciò la visione del cielo come luogo della perfezione (espressa dal moto circolare) e dell’immutabilità.
Tuttavia la concezione di un cielo perfetto e immutabile era molto radicata nella filosofia greca.

Il problema di Platone

Nel IV secolo a.C., il filosofo Platone, alla ricerca di una soluzione che salvasse l’ipotesi del moto circolare, pose ai suoi allievi il seguente problema:

"Le stelle, rappresentando oggetti eterni, divini e immutabili, si muovono con velocità uniforme intorno alla Terra, come noi possiamo constatare, e descrivono la più regolare e perfetta di tutte le traiettorie, quella della circonferenza senza fine. Ma alcuni oggetti celesti, i pianeti, vagano attraverso il cielo e seguono cammini complessi, con inclusione anche di moti retrogradi. Tuttavia, essendo corpi celesti, anch’essi devono muoversi in maniera conforme al loro rango elevato: i loro moti devono derivare da qualche combinazione di cerchi perfetti, dal momento che non descrivono esattamente cerchi perfetti. Quali sono le combinazioni di moti circolari con velocità uniforme che possono spiegare questo comportamento così particolare in un insieme coerente di moti regolari nel cielo?"

Progetto Fisica, 2, Zanichelli, Bologna 1986, pag. 13

Il tentativo di rispondere a questo tipo di domanda fece sorgere diversi modelli, detti modelli geocentrici, perché avevano in comune l’ipotesi che la Terra, concepita come sfera, fosse al centro dell’Universo.

Il modello di Eudosso

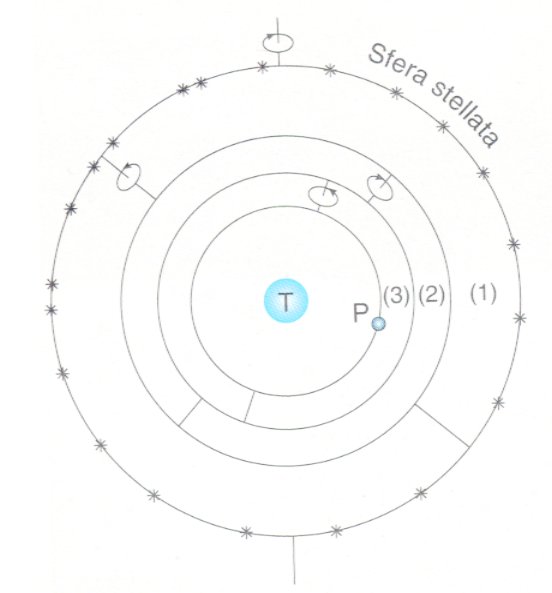
Nel modello di Eudosso (IV secolo a.C.) i corpi celesti stanno su sfere concentriche rispetto alla Terra, che è considerata immobile al centro dell’Universo. La sfera più esterna è quella delle stelle fisse e si muove di moto circolare uniforme. Gli altri corpi celesti sono localizzati su 7 gruppi di sfere (sfere omocentriche): 3 per il Sole, 3 per la Luna, 4 per ciascuno dei cinque pianeti, per un totale di 27 sfere.
Le sfere sono tutte concentriche e ciascuna di esse all’interno del proprio gruppo ruota intorno a un asse differente. Il corpo celeste relativo ad un gruppo è fissato alla sfera più interna e partecipa alla rotazione di tutte le sfere del gruppo. Con la combinazione di tutti questi moti circolari si ottengono traiettorie in grado di descrivere il moto reale dei corpi celesti.
Purtroppo il modello di Eudosso era alquanto complesso e artificioso, e inoltre, per cercare di rendere più coerente il sistema collegando tutte le sfere fra di loro necessitava l’aggiunta di altre sfere.

Il modello di Tolomeo

Nel II secolo a.C. fu formulato un secondo modello ad opera di Tolomeo di Alessandria (sistema tolemaico). Esso rimase il modello universalmente accettato fino alla rivoluzione copernicana.
Tolomeo si era prefisso di trovare un sistema capace di predire accuratamente le posizioni di ogni pianeta.
Nella prefazione del suo libro (Almagesto), egli definisce il problema ed enuncia le ipotesi da lui accettate:

"…noi desideriamo trovare le cose che appaiono evidenti e inconfutabili traendole dalle osservazioni antiche nonché da quelle da noi effettuate, e mediante dimostrazioni geometriche desideriamo utilizzare le conseguenze di queste concezioni. Inoltre, la nostra opinione è che i cieli sono sferici e che si muovono in maniera sferica; che la terra, per quanto riguarda la forma, è sensibilmente sferica…; per ciò che riguarda la sua posizione, è posta nel giusto mezzo dei cieli, a guisa di centro geometrico; per ciò che riguarda le dimensioni e la distanza, la terra è come un punto rispetto alla sfera delle stelle fisse, e non è animata da alcun moto locale."

Progetto Fisica, 2, Zanichelli, Bologna 1986, pag. 21

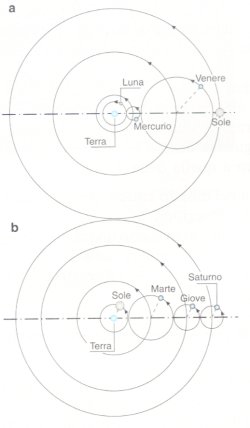
Nel modello di Tolomeo si mantiene la successione delle sfere collegate a ciascun astro, ma ciascuna ruota indipendente dalle altre.
La Terra è al centro dell’universo, ma non è sempre al centro esatto di tutti i cerchi perfetti: la Terra è in posizione eccentrica. Inoltre i corpi celesti stanno su altre sfere che hanno il loro centro sulle prime. La composizione del moto delle due sfere, l’epiciclo (quella su cui sta il pianeta) e il deferente (quella concentrica con la terra), riproduce il fenomeno del moto retrogrado e rende conto del fatto che i pianeti sono più luminosi (più vicini alla Terra) durante il moto retrogrado.
Questo modello, anche se più flessibile di quello di Eudosso, si complicò con l’aggiunta di sfere accessorie e di altre ipotesi necessarie per giustificare i dati sperimentali emergenti.


di Federica Albé

<< indietro