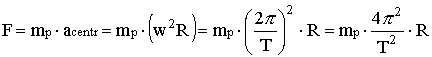
DIMOSTRAZIONE MATEMATICA DELLA LEGGE DI

GRAVITAZIONE UNIVERSALE

Newton riusci' a determinare la legge di gravitazione universale grazie alle leggi di Keplero e ai lavori di Galileo, che dicevano che i fenomeni naturali erano regolati da leggi universali.
Prima di tutto bisogna riscrivere le leggi di Keplero immaginando che le orbite dei pianeti siano circolari invece che ellittiche. Le tre leggi diventano cosi':

1°) I pianeti descrivono intorno al Sole orbite circolari aventi tutte al centro il Sole;

2°) Il moto dei pianeti e' uniforme;

3°) I quadrati dei tempi impiegati dai pianeti a descrivere le orbite sono proporzionali ai cubi dei raggi delle orbite.

I pianeti esercitano una forza sul Sole di pari modello e di verso opposto di quella che il Sole esercita su di loro. Chiamando F ed F' le forze rispettivamente del pianeta sul Sole e del Sole sul pianeta risulta:

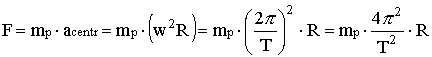
In base alla terza legge di Keplero che dice che T2 = Kr3, con K costante per tutti i pianeti, la formula diventa:

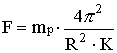
Ponendo uguale a Cs diventa:

Per lo stesso procedimento risulta:

Siccome le due forze sono uguali, allora

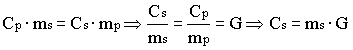
Quindi risulta che:

Ultimamente pero', grazie ai dati di un esperimento svoltosi in Antartide e all'osservazione del movimento di alcune sonde lanciate nello spazio, si e' scoperto che probabilmente la teoria della gravita' e' sbagliata. Per spiegare i fenomeni osservati sono state avanzate due ipotesi: la prima sostiene che le galassie sono formate da materia oscura, ma attualmente non si e' ancora riusciti a stabilire che cosa sia in realta' questa materia. La seconda ipotesi sostiene invece che, se la forza che agisce su di un corpo decresce fin quasi ad arrivare fino a zero, l'accelerazione ad un certo punto smette di diminuire fermandosi al valore di un decimo di miliardesimo dell'accelerazione di gravita' terrestre.
Nonostante i successi della seconda ipotesi, la comunita' scientifica non l'ha ancora accettata come valida, in quanto questo significherebbe cambiare le regole della relativita' finora esistite, ma il creatore della tesi sostiene che essa non esclude la teoria della relativita' ma anzi la completerebbe in quanto la relativita' vale per accelerazioni molto forti mentre l'altra per accelerazioni debolissime.

BIBLIOGRAFIA

Fisica 1, Bergamaschini, Marazzini, Mazzoni, Carlo Signorelli Editore;
Focus numero 99 Dicembre 2000;
Physica 1, Caforio, Ferilli, Le Monnier editore.

di Tommaso Zanzottera

<< indietro