Sessione ordinaria - Indirizzo d'ordinamento 1999
Soluzione quesito 3
a)
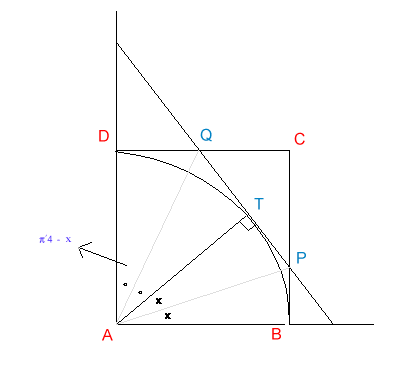
Poniamo AB = R. L'angolo BAT misura 2x quindi, essendo PT e PB tangenti alla circonferenza, l'angolo BAP misura x; si ha perciò:
Essendo poi l'angolo DAT di misura
e QD e QT tangenti alla circonferenza, gli angoli DAQ e QAT sono uguali ed hanno misura
Pertanto:
La funzione richiesta è allora:
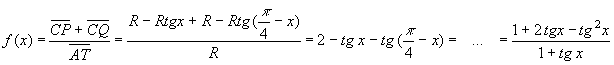
b)
Studiamo la funzione di equazione
con la
limitazione 0 £ x £ p /
4
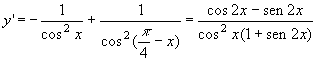
che, nell'intervallo di studio, si annulla per x = p / 8
La derivata prima risulta positiva quando
ovvero per 0 < x < p / 8
Quindi la funzione è crescente nell'intervallo 0 £ x £ p / 8 e decrescente nell'intervallo p / 8 £ x £ p / 4.
Si ha quindi un massimo per x = p / 8 che vale
.
Risulta poi:
Lo studio della derivata seconda, molto laborioso, non aggiunge particolari rilevanti
al grafico:
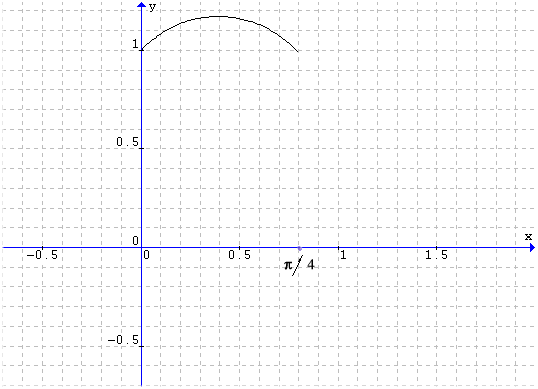
c)
Ponendo f(x) = k, consideriamo il grafico seguente:
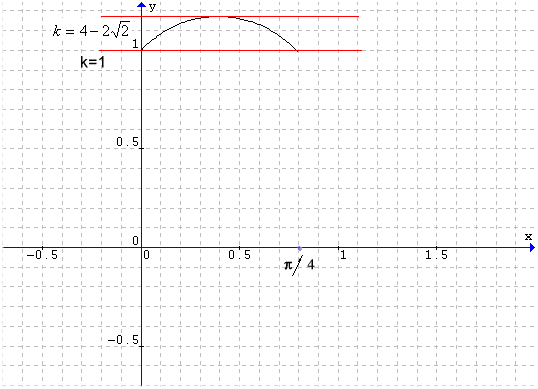
da cui emerge facilmente che si hanno sempre due soluzioni per
d)
La forma richiesta di f(x) si ottiene facilmente trasformando prima la tangente
in seno e coseno e poi applicando le formule di duplicazione e bisezione del seno e del
coseno.
e)
Stabiliamo che
Risulta: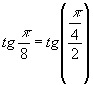 
ed essendo 
si ha:
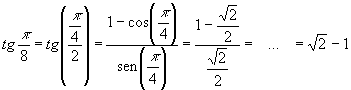
