Scuole Italiane all'Estero
E’ assegnato un cilindro equilatero Q il cui raggio di base misura a.
a) Si determini il cono C di volume minimo circoscritto al cilindro ( C e Q hanno basi complanari);
b) Si determini il valore di a per il quale il volume di C, approssimato alla prima cifra decimale, è 31,4 dm3;
c) Si determini il volume della sfera S circoscritta a C.
Nel piano riferito ad un sistema di riferimento ortogonale monometrico è data la curva G di equazione:
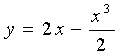
a) Si studi e si rappresenti G;
b) considerata la retta r di coefficiente angolare m passante per il punto A(2, 0), si determini, al variare di m, il numero delle intersezioni di r con G;
c) si calcoli l’area della regione finita di piano R, del primo quadrante, delimitata da G e dall’asse x;
d) si determini il volume del solido generato da R in un giro completo intorno all’asse x.
QUESTIONARIO
1. Enunciare il teorema di de L’Hôpital e applicarlo per dimostrare che:
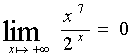
2. Mostrare, eventualmente anche con esempi, che la derivata del prodotto di due o più funzioni non è il prodotto delle derivate.
3.
Dimostrare che se un polinomio p(x) è
divisibile per (x-a)m allora ![]() è divisibile per (x-a)m-1.
è divisibile per (x-a)m-1.
4. Calcolare la derivata della funzione:
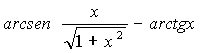
Dal risultato quali conseguenze se ne possono trarre per la f(x)? E’ una costante?
5. Si ricavi la formula che dà il numero delle combinazioni semplici di n elementi a k a k.
6. Verificare che:
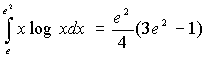
7. Siano a e b due numeri positivi diversi da 1. Dimostrare che:
![]()
8. La somma di due numeri non negativi è 16. Quale è il valore più basso che assume la somma dei loro quadrati? Quale il valore più alto?
La prova richiede lo svolgimento di uno dei due problemi proposti e le risposte a quattro domande scelte all’interno del questionario.
Durata massima della prova : 6 ore
E’ consentito l’uso della calcolatrice tascabile non programmabile e la consultazione del vocabolario d’Italiano.