ESAME DI STATO DI
LICEO SCIENTIFICO
a.s.
2002/2003
CORSO DI
ORDINAMENTO
Sessione
straordinaria
Tema di
MATEMATICA
Il candidato risolva
uno dei due problemi e 5 dei 10 quesiti in cui si articola il
questionario.
PROBLEMA 1.
È
assegnata la seguente equazione in x:
x3 + 2 x - 50 = 0 .
a) Dimostrare che ammette una ed una sola soluzione 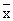 nel
campo reale.
nel
campo reale.
b) Determinare il numero intero z tale che risulti: z < 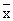 <
z + 1 .
<
z + 1 .
c) Dopo aver riferito il piano ad un sistema di assi cartesiani
ortogonali (Oxy), determinare, se esistono, i valori del parametro reale k (k¹
-1) per cui la curva Ck di equazione:
y =
(x3 + 2 x - 50) + k (x3 + 2 x - 75)
ammette un massimo e un minimo relativi.
d) Stabilire se esiste un valore 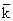 di k per cui la
curva
di k per cui la
curva 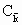 è simmetrica rispetto all'origine O.
è simmetrica rispetto all'origine O.
e) Stabilire se fra le rette di equazione y=5x+m, dove m è un
parametro reale, ve ne sono di tangenti alla curva C0 ottenuta per
k=0.
PROBLEMA 2.
La base minore, la
base maggiore e il perimetro di un trapezio isoscele misurano nell’ordine:
6 cm ,
10 cm , 4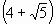 cm .
cm .
a) Dire,
giustificando la risposta, se il trapezio è circoscrittibile ad una
circonferenza.
b) Spiegare
perché il trapezio è inscrittibile in una circonferenza k.
c) Dopo aver riferito il piano del trapezio ad un conveniente
sistema di assi cartesiani ortogonali, trovare l’equazione di k.
d) Trovare l’equazione della parabola p passante per gli estremi
della base minore del trapezio e avente l’asse perpendicolare a tale base e il
vertice nel centro di k.
e)
Calcolare le aree delle regioni piane il cui la parabola p divide il
trapezio.
f)
Calcolare le aree delle regioni piane in cui la parabola p divide il cerchio
delimitato da k.
QUESTIONARIO.
1) Nell'insieme delle rette dello spazio si consideri la
relazione così definita: «due rette si dicono parallele se sono complanari e
non hanno punti comuni». Dire se è vero o falso che gode della proprietà
transitiva e fornire un'esauriente spiegazione della risposta.
2) In un piano, riferito ad un sistema monometrico di assi
cartesiani ortogonali (Oxy), è assegnato il luogo geometrico dei punti che
soddisfano alla seguente equazione:
8
x2 + 8 y2 – 4 k x + 8 y – 3 k = 0 ,
dove
k è un parametro reale. Calcolare per quali valori di k il luogo è costituito
da:
1) un
punto; 2) due punti; 3) infiniti punti; 4) nessun punto.
3) Dimostrare che condizione necessaria e sufficiente affinché
un trapezio rettangolo abbia le diagonali perpendicolari è che le misure della
base minore, dell’altezza e della base maggiore, prese nell’ordine e
considerate rispetto alla stessa unità di misura, siano numeri in progressione
geometrica.
4) Dire se è vero che risulta: 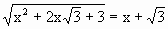 per ogni x
reale e giustificare la risposta.
per ogni x
reale e giustificare la risposta.
5) Si consideri la funzione polinomiale in x:
y =
a0 + a1 x + a2 x2 + … +
an xn .
Dimostrare che il suo grafico, rappresentato in un piano cartesiano, ha
come tangente nel punto di ascissa 0 la retta di equazione y = a0 +
a1 x .
6) Si consideri la successione di termine generale an
tale che:
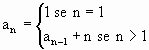 .
.
Calcolare a100 .
7) Considerata la successione di termine
generale:
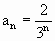 ,
,
calcolare 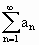 .
.
8) Considerata la funzione f(x) tale che:
f(x) =
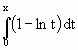 , con x > 0 ,
, con x > 0 ,
determinare i suoi zeri e gli intervalli in cui cresce o decresce.
9) Come si sa, la parte di sfera compresa fra due piani
paralleli che la secano si chiama segmento sferico a due basi. Indicati
con 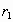 ed
ed 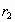 i raggi delle due
basi del segmento sferico e con h la sua altezza (distanza tra le
basi), dimostrare che il volume V del segmento sferico considerato è
dato dalla seguente formula:
i raggi delle due
basi del segmento sferico e con h la sua altezza (distanza tra le
basi), dimostrare che il volume V del segmento sferico considerato è
dato dalla seguente formula:
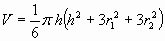 .
.
Qualunque sia il metodo seguito per la dimostrazione, esplicitare ciò che si
ammette.
10) Calcolare il seguente limite:
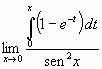 ,
,
essendo e la base dei logaritmi naturali.
___________________________
Durata massima
della prova: 6 ore.
È consentito soltanto l’uso di
calcolatrici non programmabili.
Non è ammesso
lasciare l’Istituto prima che siano trascorse tre ore dalla dettatura del tema.
![]() nel
campo reale.
nel
campo reale.
![]() <
z + 1 .
<
z + 1 .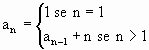 .
.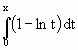 , con x > 0 ,
, con x > 0 ,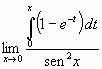 ,
,