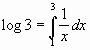ESAME DI STATO DI LICEO
SCIENTIFICO
a.s. 2002/2003
Sessione Ordinaria
CORSO SPERIMENTALE
Tema di MATEMATICA
Il candidato risolva uno dei
due problemi e 5 dei 10 quesiti proposti nel questionario.
PROBLEMA 1
Nel piano sono dati: il
cerchio g di diametro OA = a, la
retta t tangente a g in A, una retta r passante per O, il punto B,
ulteriore intersezione di r con g , il
punto C intersezione di r con t.
La parallela per B a t e la
perpendicolare per C a t s’intersecano in P. Al variare di r, P
descrive il luogo geometrico G noto con
il nome di versiera di Agnesi [ da Maria Gaetana Agnesi, matematica
milanese, (1718-1799)].
Si provi che valgono le
seguenti proporzioni:
|
OD : DB = OA
: DP
OC : DP = DP
: BC
ove D è la
proiezione ortogonale di B su OA;
Si verifichi che, con una
opportuna scelta del sistema di coordinate cartesiane ortogonali e monometriche Oxy
, l’equazione cartesiana di G è: 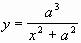 ; ;
Si tracci il grafico di G e si provi che l’area compresa fra G e il suo asintoto è quattro volte quella del
cerchio g .
|
PROBLEMA 2
Nel piano, riferito ad assi
cartesiani ortogonali e monometrici Oxy , è dato il rettangolo OABC con i
vertici A e C di coordinate rispettive (2, 0) e (0, 1). Sia P un punto sul lato OA.
Si determini la
posizione di P che massimizza l’angolo  . Si calcoli tale valore massimo e lo si
indichi con d . . Si calcoli tale valore massimo e lo si
indichi con d .
Si descrivano i luoghi
geometrici F e G dei punti del piano che vedono il lato CB sotto angoli costanti di
ampiezze rispettive d e
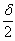
Si calcoli l’area della
regione finita di piano racchiusa tra F e
G .
|
QUESTIONARIO
1. Quale è la capacità
massima, espressa in centilitri, di un cono di apotema 2 dm?
2. Dare un esempio di
polinomio P(x) il cui grafico tagli la retta y=2 quattro volte.
3. Dimostrare, usando il teorema
di Rolle [da Michel Rolle, matematico francese, (1652-1719)], che se
l’equazione :
|

ammette
radici reali, allora fra due di esse giace almeno una radice dell’equazione :
|
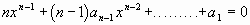
4. Dare un esempio di
solido il cui volume è dato da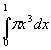 . .
5. Verificare che
l’equazione 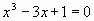 ammette tre radici reali. Di una di esse, quella compresa tra 0 e 1, se ne
calcoli un’approssimazione applicando uno dei metodi numerici studiati. ammette tre radici reali. Di una di esse, quella compresa tra 0 e 1, se ne
calcoli un’approssimazione applicando uno dei metodi numerici studiati.
6. Dopo aver illustrato il
significato di funzione periodica dare un esempio di funzione trigonometrica di periodo
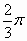
7. Nell’esperimento del
lancio di una moneta non truccata, calcolare la probabilità di avere almeno 6 teste in 9
lanci.
8. Tre scatole A, B e C
contengono lampade prodotte da una certa fabbrica di cui alcune difettose. A contiene 2000
lampade con il 5% di esse difettose, B ne contiene 500 con il 20% difettose e C ne
contiene 1000 con il 10% difettose.
Si sceglie una scatola a
caso e si estrae a caso una lampada. Quale è la probabilità che essa sia difettosa?
9. Perché "geometria
non euclidea"? Che cosa viene effettivamente negato della geometria euclidea?
10. Esporre una strategia
numerica per il calcolo approssimato di
|
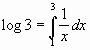
_________________________
Durata
massima della prova : 6 ore
E’
consentito l’uso della calcolatrice tascabile non programmabile e la consultazione
del vocabolario d’Italiano.
![]() ;
; 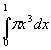 .
.