ESAME DI STATO DI LICEO
SCIENTIFICO
a.s. 2002/2003
Sessione Ordinaria
CORSO SPERIMENTALE
Tema di MATEMATICA
Il candidato risolva uno dei
due problemi e 5 dei 10 quesiti proposti nel questionario.
PROBLEMA 1
Nel piano sono dati: il
cerchio g di diametro OA = a, la
retta t tangente a g in A, una
retta r passante per O, il punto B, ulteriore intersezione di r con g , il punto C intersezione di r con t.
La parallela per B a t e la
perpendicolare per C a t s’intersecano in P. Al variare di r, P
descrive il luogo geometrico G noto con
il nome di versiera di Agnesi [ da Maria Gaetana Agnesi, matematica
milanese, (1718-1799)].
Si provi che valgono le
seguenti proporzioni:
|
OD : DB = OA
: DP
OC : DP = DP
: BC
ove D è la
proiezione ortogonale di B su OA;
Si verifichi che, con una
opportuna scelta del sistema di coordinate cartesiane ortogonali e monometriche Oxy
, l’equazione cartesiana di G è: 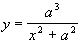 ; ;
Si tracci il grafico di G e si provi che l’area compresa fra G e il suo asintoto è quattro volte quella del
cerchio g .
|
PROBLEMA 2
Nel piano, riferito ad un
sistema di assi cartesiani ortogonali e monometrici Oxy , è dato il rettangolo OABC
con i vertici A e C di coordinate rispettive (2, 0) e (0, 1). Sia P un punto
sul lato OA.
Si determini la
posizione di P che massimizza l’angolo 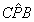 . Si calcoli tale valore massimo e lo si
indichi con d . . Si calcoli tale valore massimo e lo si
indichi con d .
Si descrivano i luoghi
geometrici F e G dei punti del piano che vedono il lato CB sotto angoli costanti di
ampiezze rispettive d e
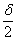
Si calcoli l’area della
regione finita di piano racchiusa tra F e
G .
|
QUESTIONARIO
1. Quante partite di
calcio della serie A vengono disputate complessivamente (andata e ritorno) nel campionato
italiano a 18 squadre?
2. Tre scatole A, B e C
contengono lampade prodotte da una certa fabbrica di cui alcune difettose. A contiene 2000
lampade con il 5% di esse difettose, B ne contiene 500 con il 20% difettose e C ne
contiene 1000 con il 10% difettose.
Si sceglie una scatola a
caso e si estrae a caso una lampada. Quale è la probabilità che essa sia difettosa?
3. Quale è la capacità
massima, espressa in centilitri, di un cono di apotema 2 dm?
4. Dare un esempio di
polinomio P(x) il cui grafico tagli la retta y=2 quattro volte.
5. Si vuole che
l’equazione
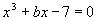
abbia tre radici reali. Quale è un possibile valore di b?
6. Dare un esempio di solido
il cui volume è dato da
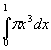 . .
7. Di una funzione f(x) si
sa che ha derivata seconda uguale a senx e che 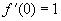 . .
Quanto vale 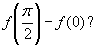
8. Dopo aver illustrato il
significato di funzione periodica dare un esempio di funzione trigonometrica di periodo
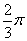
|
9. Perché
"geometria non euclidea"? Che cosa viene negato della geometria euclidea?
10. Dimostrare, usando il teorema
di Rolle [da Michel Rolle, matematico francese, (1652-1719)], che se
l’equazione :
|

ammette
radici reali, allora fra due di esse giace almeno una radice dell’equazione :
|
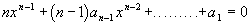
_________________________
Durata
massima della prova : 6 ore
E’
consentito l’uso della calcolatrice tascabile non programmabile e la consultazione
del vocabolario d’Italiano.
![]() ;
; 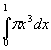 .
.