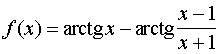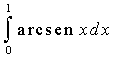ESAMI DI STATO DI LICEO SCIENTIFICO

PIANO NAZIONALE DI INFORMATICA

Sessione  2001

seconda prova scritta

Tema di MATEMATICA

Sessione suppletiva

PROBLEMA 1

             Le misure a, b, c dei lati di un triangolo ABC sono in progressione aritmetica di ragione k.

a)      Si esprima, in funzione di k, il raggio r della circonferenza inscritta nel triangolo;

b)      si stabilisca il valore di k per il quale r è massimo;

c)      si fissi nel piano del triangolo un conveniente sistema di assi cartesiani , ortogonali e monometrici, e, per il valore di k determinato in b), si scrivano le coordinate dei vertici del triangolo ABC nonché le equazioni delle circonferenze, inscritta e circoscritta, a ABC;

d)      si calcoli il rapporto tra i volumi delle due sfere di cui le circonferenze, inscritta e circoscritta, sono sezioni diametrali.

PROBLEMA 2

             Una industria commercializza un suo prodotto confezionandolo in lattine realizzate utilizzando fogli di una lamierina molto sottile. Ciascuna lattina, di assegnata capacità, ha la forma di un cilindro circolare retto.

Trascurando lo spessore del materiale, il candidato determini:

a)      le dimensioni della lattina per la quale occorre la minima quantità di materiale per realizzarla.

Successivamente, posto il volume della lattina pari a 2 decilitri, se ne esplicitino le misure delle dimensioni:

b)      nel caso di cui al punto a);

c)      nel caso in cui si voglia che il diametro della base sia sezione aurea dell’altezza.

QUESTIONARIO

1.      Enunciare il teorema del valor medio o di Lagrange illustrandone il legame con il teorema di Rolle  e le implicazioni ai fini della determinazione della crescenza o decrescenza delle curve.

2.      Calcolare la derivata della funzione

Quali conclusioni se ne possono trarre per la f(x)?

3.      Dire qual è il dominio della funzione  e stabilire il segno della derivata prima e quello della derivata seconda di f(x) nel punto  .

4.      Calcolare, integrando per parti:

5.      Spiegare, anche con esempi appropriati, il significato in matematica di “concetto primitivo” e di “assioma” .

6.      Nell’insieme delle cifre 1,2,3,………..,9  se ne scelgono due a caso. La loro somma è pari: determinare la probabilità che entrambe le cifre siano dispari.

7.      Verificato che l’equazione ammette una sola radice reale compresa tra 2 e 3, se ne calcoli un’approssimazione applicando uno dei metodi numerici studiati.

8.      Calcolare il rapporto tra la superficie totale di un cilindro equilatero e la superficie della sfera ad esso circoscritta.

9.      Dire (motivando la risposta) se è possibile inscrivere in una semicirconferenza un triangolo che non sia rettangolo. Ovvero, con i versi di Dante:

 ..… se del mezzo cerchio far si puote

triangol sì ch’ un retto non avesse.  (Paradiso, XIII, 101-102)

_______________________________

La prova richiede lo svolgimento di uno dei due problemi proposti e le risposte a cinque domande scelte all’interno del questionario.

Durata massima della prova : 6 ore

E’ consentito l’uso della calcolatrice tascabile non programmabile e la consultazione del vocabolario d’Italiano.