Maturitā sperimentale 1995-96

(Sessione suppletiva)

l. Si consideri in un piano, riferito ad un sistema di assi cartesiani ortogonali Oxy, il settore

circolare T del primo quadrante, appartenente al cerchio delimitato dalla circonferenza di

equazione x² + y² = r² , tale che i raggi che lo individuano siano sull'asse x e sulla retta di equazione .

Il candidato:

a) calcoli il volume V₁, e V'₁ dei solidi ottenuti dalla rotazione completa di T rispettivamente intorno all'asse x e all'asse y;

b) determini, utilizzando il teorema di Guldino, le coordinate del baricentro del settore;

c) considerati i punti A (r, 0 ) e C ( 1 /2, 0 ) e detti 0', C' le rispettive proiezioni dei punti 0, C sulla retta 1 di equazione y = 1, esprima in funzione di r il rapporto

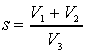
essendo V₂ il volume del cono ottenuto dalla rotazione completa del triangolo OAO' intorno all'asse y e V₃ il volume del cono ottenuto dalla rotazione completa del triangolo ACC' intorno alla retta CC';

d) studi come varia il suddetto rapporto al variare del raggio r della circonferenza e rappresenti in un piano riferito ad un sistema di assi cartesiani ortogonali O'rs il grafico della funzione s(r).

2. In un piano riferito ad un sistema di assi cartesiani ortogonali 0 xy č assegnata la parabola

p avente per asse di simmetria l'asse x e passante per i punti A (0, -l) e B (-2, 0). Siano r una retta parallela all'asse y, H il suo punto d'intersezione con l'asse x e Q e R i suoi punti d'intersezione con la parabola p.

Il candidato

a) esprima in funzione dell'ascissa di H l'area S del triangolo OQR e studi come essa varia al variare di r;

b) dica qual č l'insieme descritto dall'ascissa di H quando esistono 3 triangoli OQR tra loro equivalenti;

c) determini con l'approssimazione di 1/10 gli estremi dell'intervallo descritto dall'ascissa di H quando esiste un solo triangolo OQR la cui area S č minore di 1;

d) descriva una procedura che consenta di calcolare i valori approssimati di tali estremi con un'approssimazione di 10^-n (con n appartenente ad N) e la codifichi in un linguaggio di programmazione conosciuto.

3. Al servizio di soccorso stradale di una certa cittā, aperto 24 ore su 24, arrivano in media 48 chiamate al giorno, due in media all'ora, secondo una distribuzione di Poisson.

Il candidato

a) calcoli la probabilitā che nella prima ora arrivino almeno 2 chiamate;

b) calcoli la probabilitā che il tempo di attesa fino alla prima chiamata di un certo giorno sia di almeno 1 ora;

c) tenendo presente che il 45% delle chiamate č effettuato da donne che nel 90% dei casi richiedono l'intervento del carro attrezzi, mentre tale intervento č richiesto dagli uomini nel 75% dei casi, determini, se si registra una richiesta di intervento di carro attrezzi, qual č la probabilitā che la richiesta sia stata effettuata da un uomo;

d) calcoli qual č il numero medio di richieste di carro attrezzi per ora.

Soluzione terzo quesito (quesito3.jpg- quesito3.PDF)