-----I Problemi proposti dai lettori -----

Siano date due circonferenze secanti. Su una delle due circonferenze si individui un punto P non interno al secondo cerchio. Si traccino da P le semirette passanti per i due punti di secanza. Tali semirette intersecheranno la seconda circonferenza nei punti A e B. Dimostrare che la retta passante per i punti A e B è parallela alla retta tangente nel punto P.

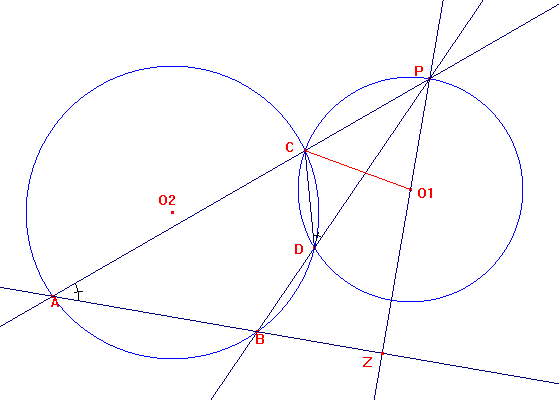
Chiamiamo O1 il centro della circonferenza su cui giace P,  C il punto di 
secanza sulla retta PA,
D il punto di secanza sulla retta PB, Z l'intersezione tra le rette O1P e 
AB.

Per la ciclicità del quadrilatero ACDB avremo
^CAB + ^CDB = pi
ma è anche
^CDP + ^CDP = pi

dunque ^CAB = ^CDP

Per il teorema dell'angolo al centro,

^CO1P = 2 ^CDP

e poichè CO1P è isoscele,

^CPZ + ^CAZ = pi/2
ovvero ^AZP = pi/2

ciò implica che la retta AB è perpendicolare alla retta O1P, dunque 
parallela alla tangente per P.