SOLUZIONISOLUZIONI

1

In un sistema di riferimento cartesiano ortogonale e monometrico si consideri il triangolo di vertici A=(-2;0), B=(2;0) e C=(1;3). Da un punto generico D di AB si conduca la perpendicolare al lato AB e si indichino rispettivamente con E ed F i punti in cui essa interseca le rette BC ed AC.

Si trovi il luogo dei punti P allineati con E ed F, tali che

e lo si studi.

SOLUZIONE DELL'AUTORE

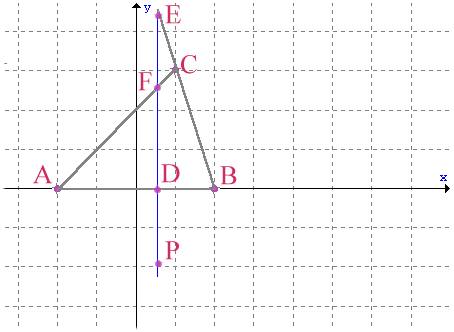
A=(-2;0) ; B=(2;0) ; C=(1;3)

D=(x;0) con -2<x<2

P=(x;y)

retta AC: y=x+2 ====> F=(x;x+2)

retta BC: y=-3x+6 ====> E=(x;-3x+6)

====> y²=(x+2)(-3x+6) ====> 3x²+y²-12=0

che è un'ellisse di semiassi

a=2

semidistanza focale

ed eccentricità

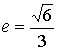
N.B. L'ellisse trovata passa per i punti A, B e C.

Approfondimento: costruire con riga e compasso un punto P soddisfacente la relazione data.

2

Scrivere un programma in Pascal che permetta di risolvere il seguente problema:

Data la conica di equazione

a) stabilire quando è un'ellisse o un'iperbole;
b) trovare le coordinate del centro;
c) calcolare l'eccentricità.

SOLUZIONE DELL'AUTORE

Program Ellisse_Iperbole;

Uses Crt;

Var a,b,c,d,e,f,xc,yc,a1,b1,a2,b2,ecc,cf:real;
risposta:char;

(*------------------------------------------------------------------------*)
Procedure presentazione;

Begin
Clrscr;
TextColor(white);
Writeln('Questo programma stabilisce se la conica di equazione');
Writeln;
Writeln(' Ax²+By²+Cx+Dy+E=0');
Writeln;
Writeln('è un''ellisse o un''iperbole, trova il centro e l''eccentricità');
GotoXy(40,20);
TextColor(yellow+blink);
Writeln('......< ENTER > per iniziare ');
Readln
End;

(*------------------------------------------------------------------------*)
Procedure InserisciDati;

Begin
Repeat
ClrScr;
TextColor(cyan);
Writeln('A x ² + B y² + C x + D y + E = 0 ' );
Writeln;TextColor(white);
Writeln('Inserisci i coefficienti');
Writeln;Writeln;
Write('A = '); Readln(a);
Write('B = '); Readln(b);
Write('C = '); Readln(c);
Write('D = '); Readln(d);
Write('E = '); Readln(e);
Writeln;Writeln;
If (a=0) or (b=0) then
begin
TextColor(red);
Writeln('A e B non possono essere nulli !');
Writeln;
Writeln(' ......< enter > per continuare');
Readln
end
Until (a<>0) and (b<>0)
End;
(*------------------------------------------------------------------------*)

Procedure elabora;

Begin
xc:=-c/(2*a);
yc:=-d/(2*b);
a1:=a;
b1:=b;
f:=a*xc*xc+b*yc*yc+c*xc+d*yc+e;
a2:=-f/a;
b2:=-f/b;
a:=sqrt(abs(a2));
b:=sqrt(abs(b2));

End;

(*------------------------------------------------------------------------*)

Procedure centro;

Begin

textcolor(yellow);
Writeln('Il centro è ------> Centro (',xc:5:2,';',yc:5:2,')');
Writeln;
Writeln('L''eccentricità è ------> e = ',ecc:5:2);
Textcolor(cyan);
If ecc=0 then
Writeln('Si tratta di una circonferenza')
end;

(*------------------------------------------------------------------------*)

Procedure Comunica;

Begin
textcolor(magenta);
If a1*b1>0 then
begin
Writeln('La conica è un''ellisse');
Textcolor(white);
Writeln('La sua forma canonica è');textcolor(magenta);
Writeln('(',a1:5:2,')x²+(',b1:5:2,')y²+(',f:5:2,')=0');
textcolor(white);
If a*b*f<0 then
begin
Writeln('Quindi è reale');
centro
end
ELSE
Writeln('Quindi è immaginaria')
end
ELSE
begin
Writeln('La conica è un''iperbole');
centro
end

end;

(*------------------------------------------------------------------------*)

Procedure iperbole;

Begin
elabora;
cf:=sqrt(a*a+b*b);
If a2>0 then
ecc:=cf/a ELSE
ecc:=cf/b;
comunica
End;

(*------------------------------------------------------------------------*)

Procedure ellisse;

Begin
elabora;

If a>b then
begin
cf:=sqrt(a*a-b*b);
ecc:=cf/a
end
ELSE
begin
cf:=sqrt(b*b-a*a);
ecc:=cf/b
end;
comunica

End;

(*------------------------------------------------------------------------*)

Procedure riconoscimento;

Begin

If a*b>0 then ellisse ELSE
iperbole;
end;

(*------------------------------------------------------------------------*)

BEGIN (* MAIN *)

Presentazione;
Repeat
InserisciDati;
Riconoscimento;
Writeln;Writeln;Textcolor(red+blink);
Write(' ...............Ancora ? ( s / n ) ');
Readln(risposta)
Until (risposta='n') or (risposta='N')

END. (*fine main*)

3

Detti F ed F' i fuochi di un'ellisse e P un suo punto qualsiasi distinto dai vertici, siano M ed N i punti medi rispettivamente di FP ed F'P.

Si trovi l'eccentricità dell'ellisse sapendo che il quadrilatero FMNF' è circoscrittibile ad una circonferenza.

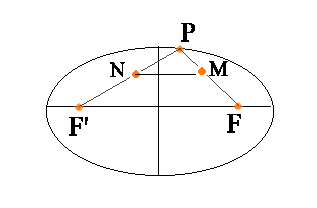Risulta (condizione di circoscrittibilità di un quadrilatero) FF'+MN=FM+F'N=(FP+F'P)/2=2a/2=a FF'=2c MN=FF'/2 =c (proprietà triangoli), quindi 2c+c=a ===> 3c=a ===> e=c/a=1/3