SOLUZIONISOLUZIONI

1999

1

I voti di un compito in classe di Matematica sono stati dall'1 al 10. Il voto medio è stato 6.7 e lo scarto quadratico medio è stato 1.2. Nell'ipotesi che i voti siano distribuiti secondo la legge normale, determinare:

a) la percentuale di studenti che ha preso il voto 6;

b) il voto massimo del peggior 10%;

c) il voto minimo del miglior 10%.

La soluzione dell'autore

a)
Indichiamo con X la variabile "voti"; per applicare la distribuzione normale è necessario trattare tale variabile come continua; quindi il voto 6 si considera come un voto dell'intervallo 5.5 < x < 6.5

La legge di di Gauss sulla distribuzione normale è data da:

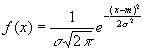
Per calcolare la probabilità P(5.5<X<6.5) con m = 6.7   e  s = 1.2 passiamo alla variabile standardizzata

Il voto 5.5 diventa -1.0

il voto 6.5 diventa -0.17

Servendosi delle apposite tavole si ha che la probabilità richiesta è data da:

P(-1.0 < T < -0.17) = P(0 < T < 1) - P(0 < T < 0.17) = 0.3413 - 0.0675 = 0.2738 = 27 % che rappresenta la percentuale degli studenti che ha preso il voto 6.

b)
Indichiamo con t_max il voto massimo richiesto in unità standard si ha che:

P( T < t_max) = 0.10

ovvero

P(t_max < T < 0) = 0.40

Dalle tabelle apposite si trova che

t_max =  -1.28

Utilizzando la formula

passiamo alla variabile X, ottenendo 5.2: il voto massimo del peggior 10 % è quindi circa 5.

c)

Detto t_min il voto minimo richiesto, per l'evidente simmetria col caso precedente si ottiene t_min = 1.28.

Passando alla variabile X otteniamo 8.2: il voto minimo del miglior 10 % è quindi circa 8.