



Questo metodo permette di calcolare in modo approssimato ∫ₐᵇ f(x) dx: 1. Suddivisione dell'intervallo [a, b] in n parti uguali: ➔ h = (b - a)/n (ampiezza passo) 2. Calcolo delle aree dei trapezi: ▷ Area trapezio i-esimo: (f(xᵢ) + f(xᵢ₊₁)) * h / 2 3. Formula composita: Tₙ = h/2 [f(x₀) + 2(f(x₁) + f(x₂) + ... + f(xₙ₋₁)) + f(xₙ)] 4. Errore: metodo più preciso di quello dei rettangoli.
Questo metodo permette di calcolare in modo approssimato ∫ₐᵇ f(x) dx: Due varianti principali (per funzione crescente): ❶ Rettangoli inscritti (somma inferiore): approssimazione per difetto ❷ Rettangoli circoscritti (somma superiore): approssimazione per eccesso Procedimento: 1. Suddivisione in n intervalli: h = (b - a)/n 2. Scelta del punto campione: - Inscritti: punto iniziale (xᵢ) - Circoscritti: punto finale (xᵢ₊₁) Formule: ▷ R(i)= h * Σ f(xᵢ) per i = 0 a n-1 (inscritti) ▷ R(c) = h * Σ f(xᵢ) per i = 1 a n (circoscritti) Due varianti principali (per funzione decrescente): ❶ Rettangoli inscritti (somma inferiore): approssimazione per difetto ❷ Rettangoli circoscritti (somma superiore): approssimazione per eccesso Procedimento: 1. Suddivisione in n intervalli: h = (b - a)/n 2. Scelta del punto campione: - Circoscritti: punto iniziale (xᵢ) - Inscritti: punto finale (xᵢ₊₁) Formule: ▷ R(c)= h * Σ f(xᵢ) per i = 0 a n-1 (circoscritti) ▷ R(i) = h * Σ f(xᵢ) per i = 1 a n (inscritti) Si prende come valore approssimato dell'integrale la media aritmetica. Media: (R(i) + R(c))/2. Errore: metodo meno preciso di quello dei trapezi.
Rappresentiamo, come aiuto grafico, la funzione (che è un'iperbole equilatera traslata) insieme alla regione la cui area è data dall'integrale da calcolare. Calcolo analitico: ∫₂⁴ 1/(x-1) dx = [ln|x-1|]₂⁴ = ln(3) - ln(1) = ln(3) ≈ 1.0986

Mostriamo il grafico, anche se non è necessario per il calcolo richiesto.
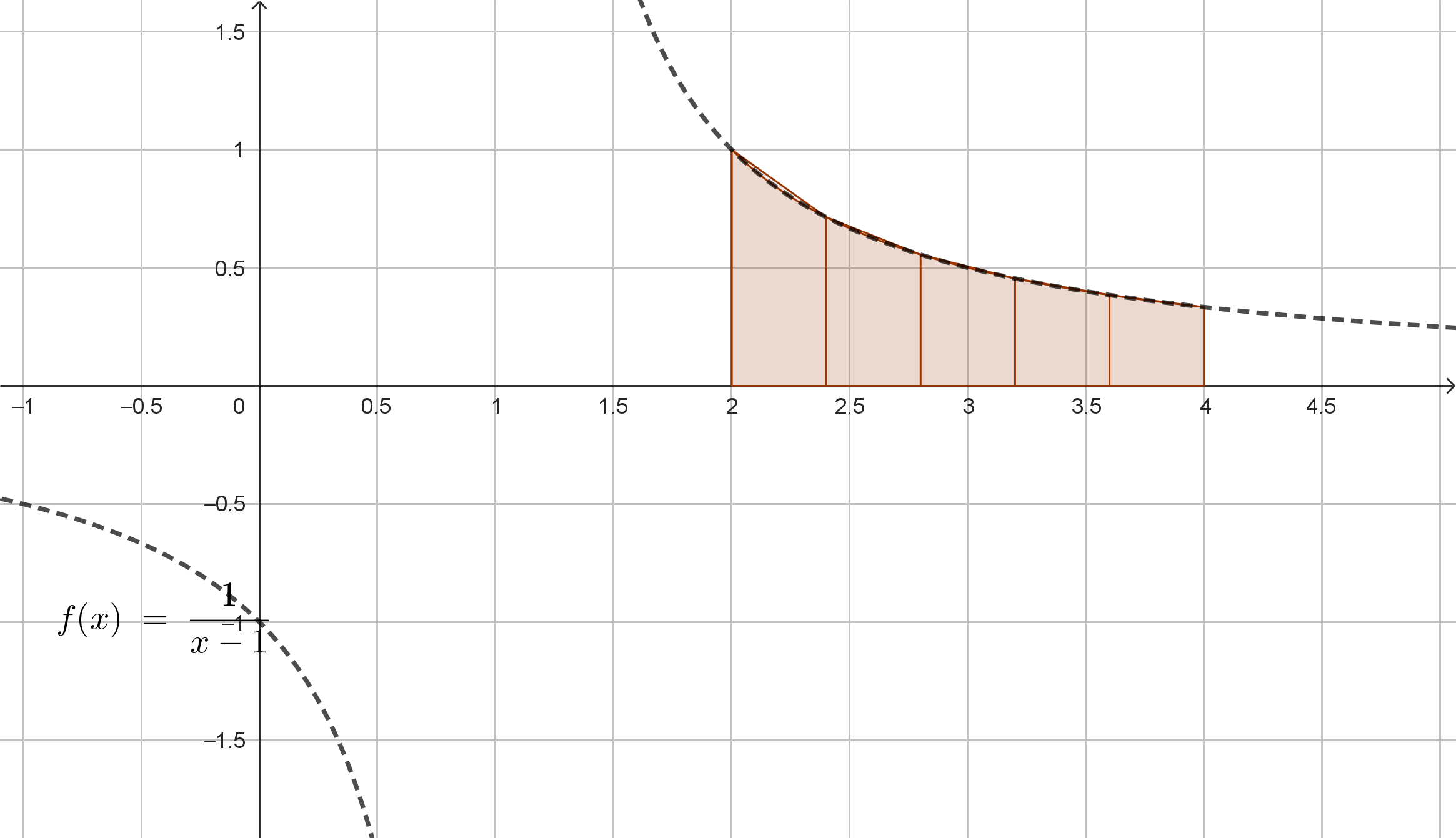 METODO DEI TRAPEZI (n=5):
h = (4-2)/5 = 0.4
x₀=2.0 (1.0000)
x₁=2.4 (0.7143)
x₂=2.8 (0.5556)
x₃=3.2 (0.4545)
x₄=3.6 (0.3846)
x₅=4.0 (0.3333)
T₅ = 0.4/2 × [1 + 2(0.7143 + 0.5556 + 0.4545 + 0.3846) + 0.3333]
= 0.2 × [1 + 4.218 + 0.3333]
= 0.2 × 5.5513 ≈ 1.11
METODO DEI TRAPEZI (n=5):
h = (4-2)/5 = 0.4
x₀=2.0 (1.0000)
x₁=2.4 (0.7143)
x₂=2.8 (0.5556)
x₃=3.2 (0.4545)
x₄=3.6 (0.3846)
x₅=4.0 (0.3333)
T₅ = 0.4/2 × [1 + 2(0.7143 + 0.5556 + 0.4545 + 0.3846) + 0.3333]
= 0.2 × [1 + 4.218 + 0.3333]
= 0.2 × 5.5513 ≈ 1.11
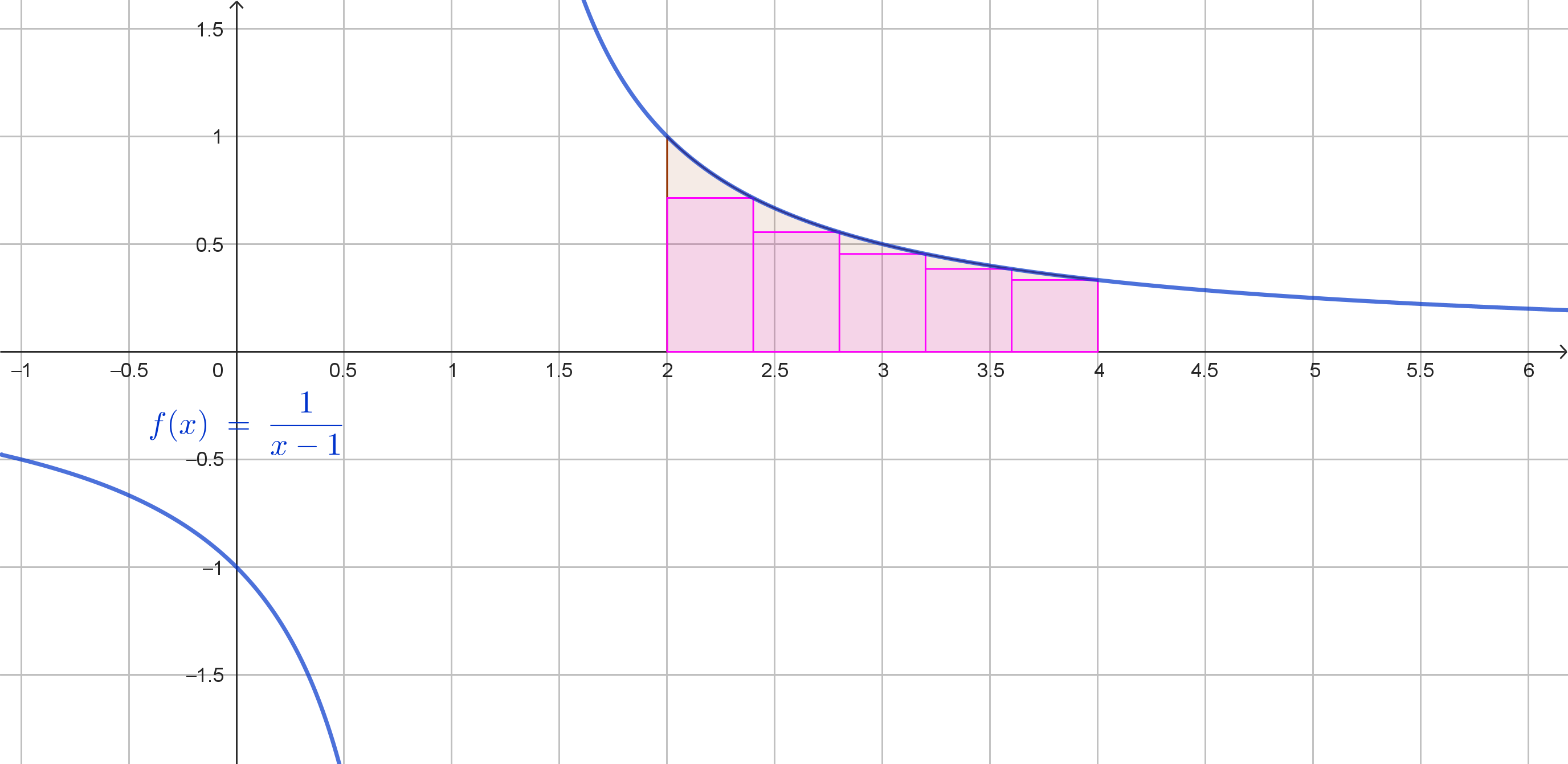
METODO DEI RETTANGOLI (n=5):
h = 0.4
Rettangoli inscritti.
Mostriamo il grafico, anche se non è necessario per il calcolo richiesto.
 2.4 (0.7143)
2.8 (0.5556)
3.2 (0.4545)
3.6 (0.3846)
4.0 (0.3333)
Somma = 0.7143 + 0.5556 + 0.4545 + 0.3846 + 0.3333 = 2.4423
R(i) = 0.4 × 2.4423 ≈ 0.98
Rettangoli circoscritti.
Mostriamo il grafico, anche se non è necessario per il calcolo richiesto.
2.4 (0.7143)
2.8 (0.5556)
3.2 (0.4545)
3.6 (0.3846)
4.0 (0.3333)
Somma = 0.7143 + 0.5556 + 0.4545 + 0.3846 + 0.3333 = 2.4423
R(i) = 0.4 × 2.4423 ≈ 0.98
Rettangoli circoscritti.
Mostriamo il grafico, anche se non è necessario per il calcolo richiesto.
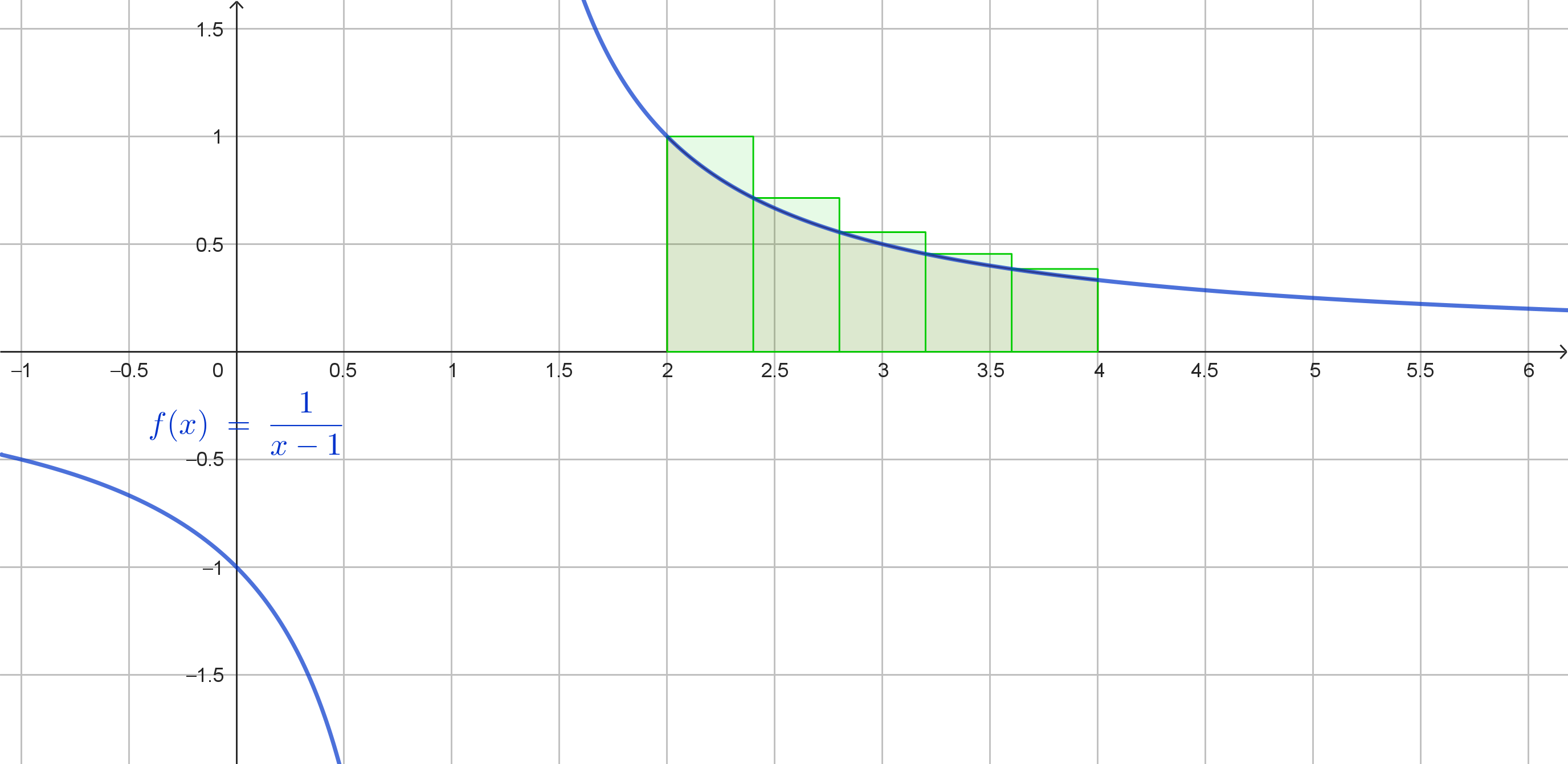 2.0 (1.0000)
2.4 (0.7143)
2.8 (0.5556)
3.2 (0.4545)
3.6 (0.3846)
Somma = 1 + 0.7143 + 0.5556 + 0.4545 + 0.3846 = 3.109
R(c) = 0.4 × 3.109 ≈ 1.24
Media: (1.24 + 0.98)/2 = 1.11
2.0 (1.0000)
2.4 (0.7143)
2.8 (0.5556)
3.2 (0.4545)
3.6 (0.3846)
Somma = 1 + 0.7143 + 0.5556 + 0.4545 + 0.3846 = 3.109
R(c) = 0.4 × 3.109 ≈ 1.24
Media: (1.24 + 0.98)/2 = 1.11
Mostriamo il grafico della funzione, anche se non è necessario per il calcolo richiesto.
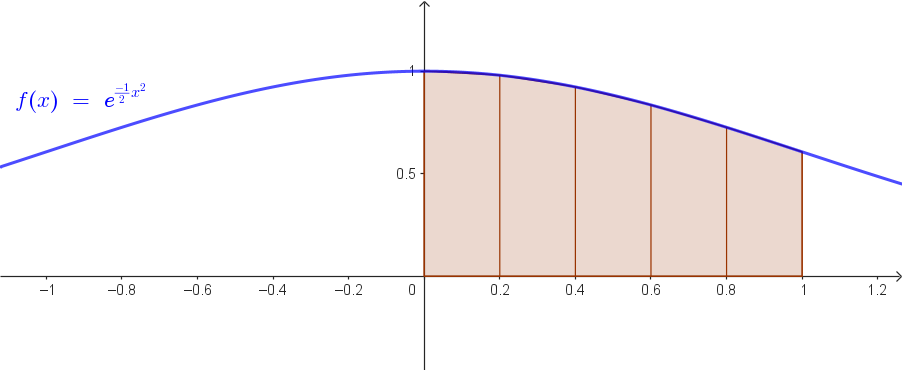 Funzione:
f(x) = e−12x²
Intervallo: [0, 1], n=5
Parametri:
h = 1 − 05 = 0.2
Punti di suddivisione:
x₀=0.0, x₁=0.2, x₂=0.4, x₃=0.6, x₄=0.8, x₅=1.0
Calcolo valori:
f(0.0) = e⁰ = 1.0000
f(0.2) = e−12(0.2)² ≈ 0.9802
f(0.4) = e−12(0.4)² ≈ 0.9231
f(0.6) = e−12(0.6)² ≈ 0.8353
f(0.8) = e−12(0.8)² ≈ 0.7261
f(1.0) = e−12(1.0)² ≈ 0.6065
Applicazione formula:
T₅ = 0.2/2 × [1 + 2×(0.9802 + 0.9231 + 0.8353 + 0.7261) + 0.6065]
= 0.1 × [1 + 2×3.4647 + 0.6065]
= 0.1 × [1 + 6.9294 + 0.6065]
= 0.1 × 8.5359 ≈ 0.8536 ≈ 0.85
Funzione:
f(x) = e−12x²
Intervallo: [0, 1], n=5
Parametri:
h = 1 − 05 = 0.2
Punti di suddivisione:
x₀=0.0, x₁=0.2, x₂=0.4, x₃=0.6, x₄=0.8, x₅=1.0
Calcolo valori:
f(0.0) = e⁰ = 1.0000
f(0.2) = e−12(0.2)² ≈ 0.9802
f(0.4) = e−12(0.4)² ≈ 0.9231
f(0.6) = e−12(0.6)² ≈ 0.8353
f(0.8) = e−12(0.8)² ≈ 0.7261
f(1.0) = e−12(1.0)² ≈ 0.6065
Applicazione formula:
T₅ = 0.2/2 × [1 + 2×(0.9802 + 0.9231 + 0.8353 + 0.7261) + 0.6065]
= 0.1 × [1 + 2×3.4647 + 0.6065]
= 0.1 × [1 + 6.9294 + 0.6065]
= 0.1 × 8.5359 ≈ 0.8536 ≈ 0.85
Funzione:
f(x) = e−12x²
Intervallo: [0, 1], n=5
Parametri:
h = 0.2
Rettangoli inscritti.
Mostriamo il grafico della funzione, anche se non è necessario per il calcolo richiesto.
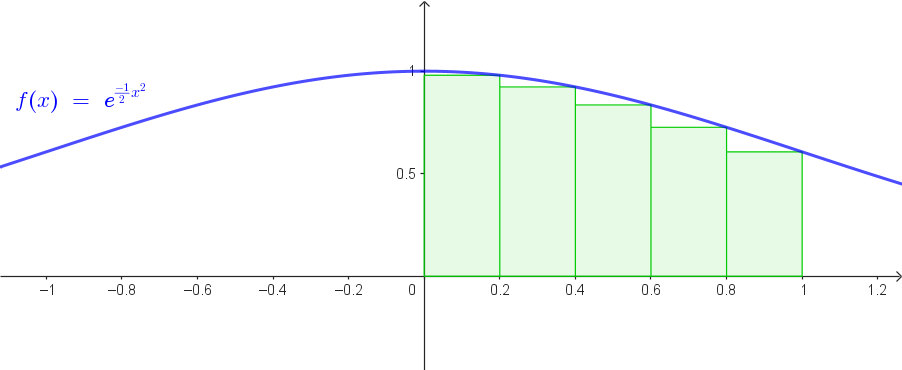 0.2 (e−12(0.2)²),
0.4 (e−12(0.4)²),
0.6 (e−12(0.6)²),
0.8 (e−12(0.8)²),
1.0 (e−12(1.0)²)
Somma = 0.9802 + 0.9231 + 0.8353 + 0.7261 + 0.6065 = 4.0712
R(i) = 0.2 × 4.0712 ≈ 0.8142 ≈ 0.81
Rettangoli circoscritti.
Mostriamo il grafico della funzione, anche se non è necessario per il calcolo richiesto.
0.2 (e−12(0.2)²),
0.4 (e−12(0.4)²),
0.6 (e−12(0.6)²),
0.8 (e−12(0.8)²),
1.0 (e−12(1.0)²)
Somma = 0.9802 + 0.9231 + 0.8353 + 0.7261 + 0.6065 = 4.0712
R(i) = 0.2 × 4.0712 ≈ 0.8142 ≈ 0.81
Rettangoli circoscritti.
Mostriamo il grafico della funzione, anche se non è necessario per il calcolo richiesto.
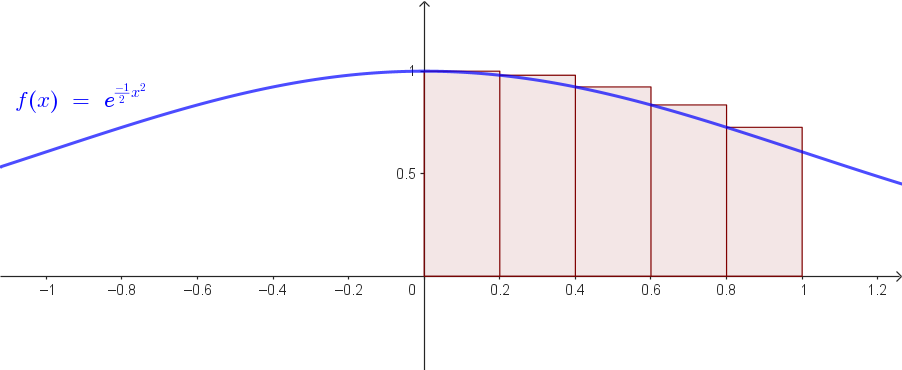 0.0 (1.0000), 0.2 (e−12(0.2)²),
0.4 (e−12(0.4)²),
0.6 (e−12(0.6)²),
0.8 (e−12(0.8)²)
Somma = 1 + 0.9802 + 0.9231 + 0.8353 + 0.7261 = 4.4647
R(c) = 0.2 × 4.4647 ≈ 0.8929 ≈ 0.89
Media dei due metodi:
(0.89 + 0.81)/2 = 0.85
0.0 (1.0000), 0.2 (e−12(0.2)²),
0.4 (e−12(0.4)²),
0.6 (e−12(0.6)²),
0.8 (e−12(0.8)²)
Somma = 1 + 0.9802 + 0.9231 + 0.8353 + 0.7261 = 4.4647
R(c) = 0.2 × 4.4647 ≈ 0.8929 ≈ 0.89
Media dei due metodi:
(0.89 + 0.81)/2 = 0.85
 1. Riscriviamo il denominatore completando il quadrato:
x2+4x+5 = (x+2)2 + 1
2. L'integrale diventa:
∫-2-11(x+2)2+1dx
3. Riconosciamo la forma ∫1u2+1du = arctan(u) + C
4. Calcoliamo:
[arctan(x+2)]-2-1 = arctan(1) - arctan(0)
= π4 - 0 = π4 ≈ 0.7854
1. Riscriviamo il denominatore completando il quadrato:
x2+4x+5 = (x+2)2 + 1
2. L'integrale diventa:
∫-2-11(x+2)2+1dx
3. Riconosciamo la forma ∫1u2+1du = arctan(u) + C
4. Calcoliamo:
[arctan(x+2)]-2-1 = arctan(1) - arctan(0)
= π4 - 0 = π4 ≈ 0.7854
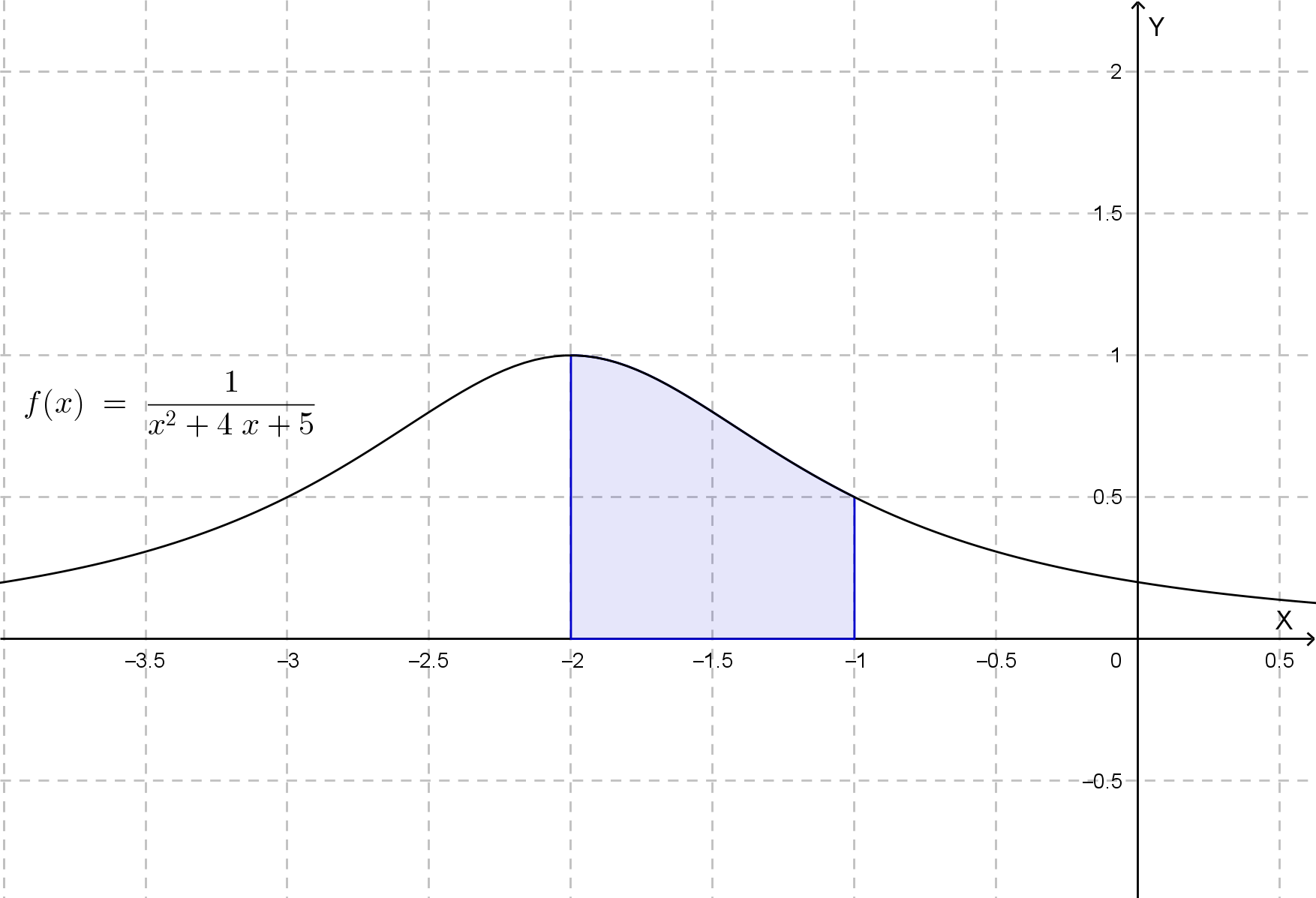
Abbiamo indicato il grafico della funzione, per comodità visiva, anche se non è necessario per il calcolo richiesto. Consideriamo la funzione f(x) = 1x2+4x+5 e calcoliamo ∫-2-1f(x)dx con n=5: 1. Calcolo passo h: h = -1 - (-2)5 = 15 = 0.2 2. Punti di suddivisione: x₀ = -2.0, x₁ = -1.8, x₂ = -1.6, x₃ = -1.4, x₄ = -1.2, x₅ = -1.0 3. Valori della funzione: f(-2.0) = 1/((-2)2+4(-2)+5) = 1/(4-8+5) = 1 f(-1.8) ≈ 0.9615 f(-1.6) ≈ 0.8621 f(-1.4) ≈ 0.7353 f(-1.2) ≈ 0.6098 f(-1.0) = 1/(1 + (-4)+5) = 0.5 4. Applicazione formula: T₅ = 0.2 × [1 + 0.52 + 0.9615 + 0.8621 + 0.7353 + 0.6098] = 0.2 × [0.75 + 3.1687] = 0.2 × 3.9187 ≈ 0.784
Consideriamo la funzione f(x) = 1x2+4x+5
e calcoliamo ∫-2-1f(x)dx con n=5.
Calcolo passo h:
h = -1 - (-2)5 = 15 = 0.2
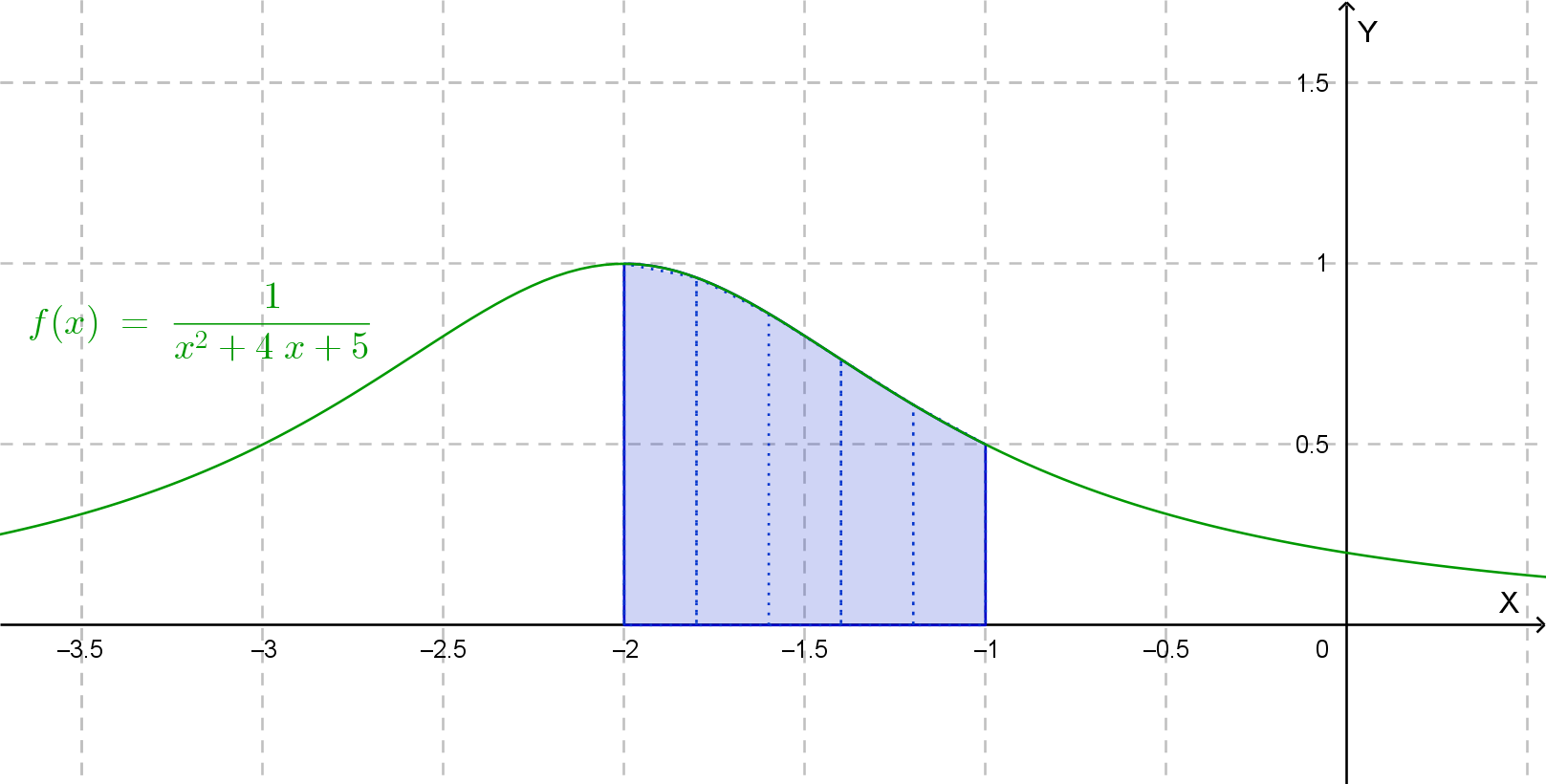
1. Rettangoli inscritti.
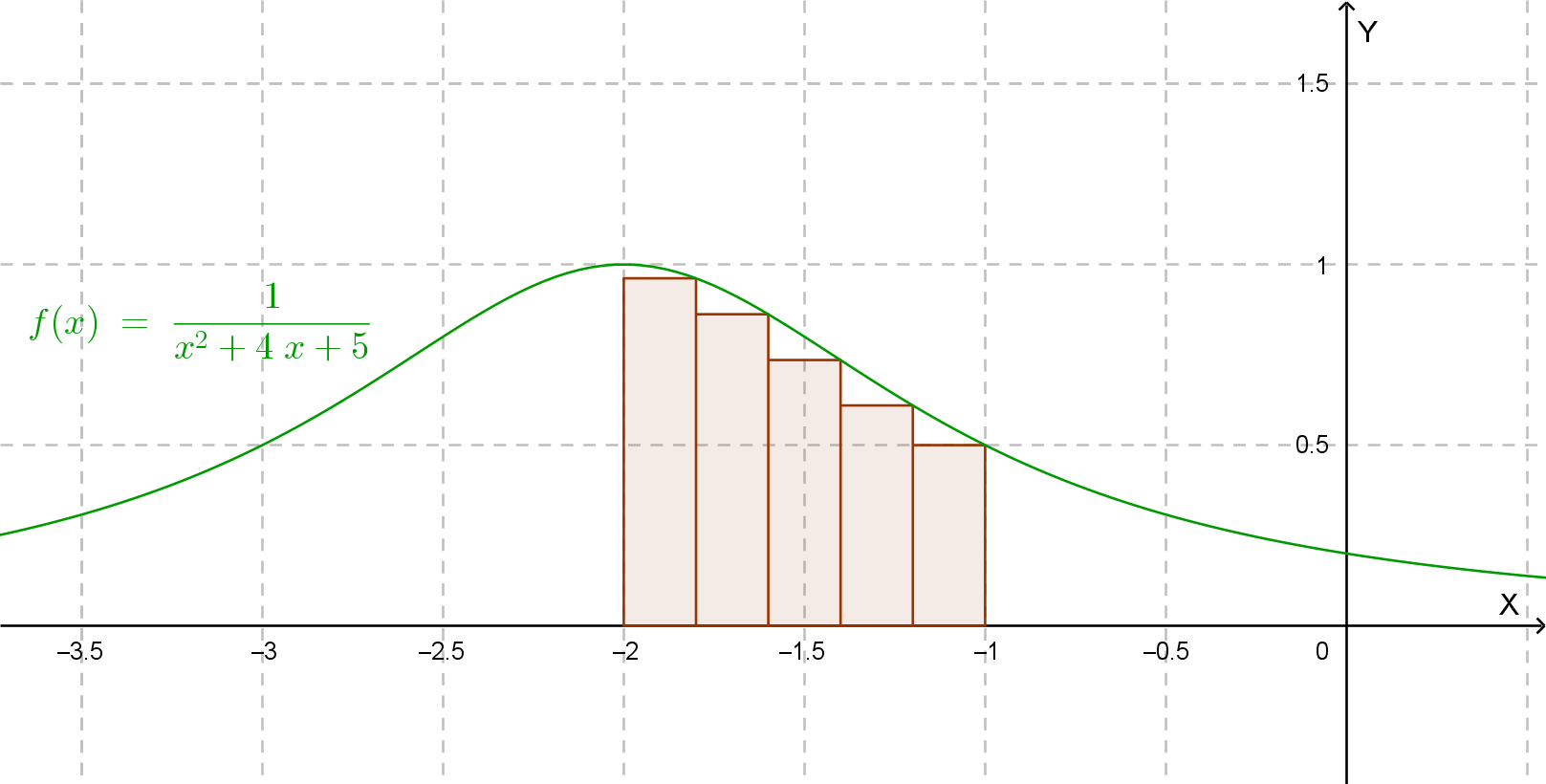 Valori: f(-1.8)≈0.9615, f(-1.6)≈0.8621,
f(-1.4)≈0.7353, f(-1.2)≈0.6098, f(-1.0)=0.5
Somma = 0.9615 + 0.8621 + 0.7353 + 0.6098 + 0.5 = 3.6687
R(i)= 0.2 × 3.6687 ≈ 0.7337
2. Rettangoli circoscritti.
Valori: f(-1.8)≈0.9615, f(-1.6)≈0.8621,
f(-1.4)≈0.7353, f(-1.2)≈0.6098, f(-1.0)=0.5
Somma = 0.9615 + 0.8621 + 0.7353 + 0.6098 + 0.5 = 3.6687
R(i)= 0.2 × 3.6687 ≈ 0.7337
2. Rettangoli circoscritti.
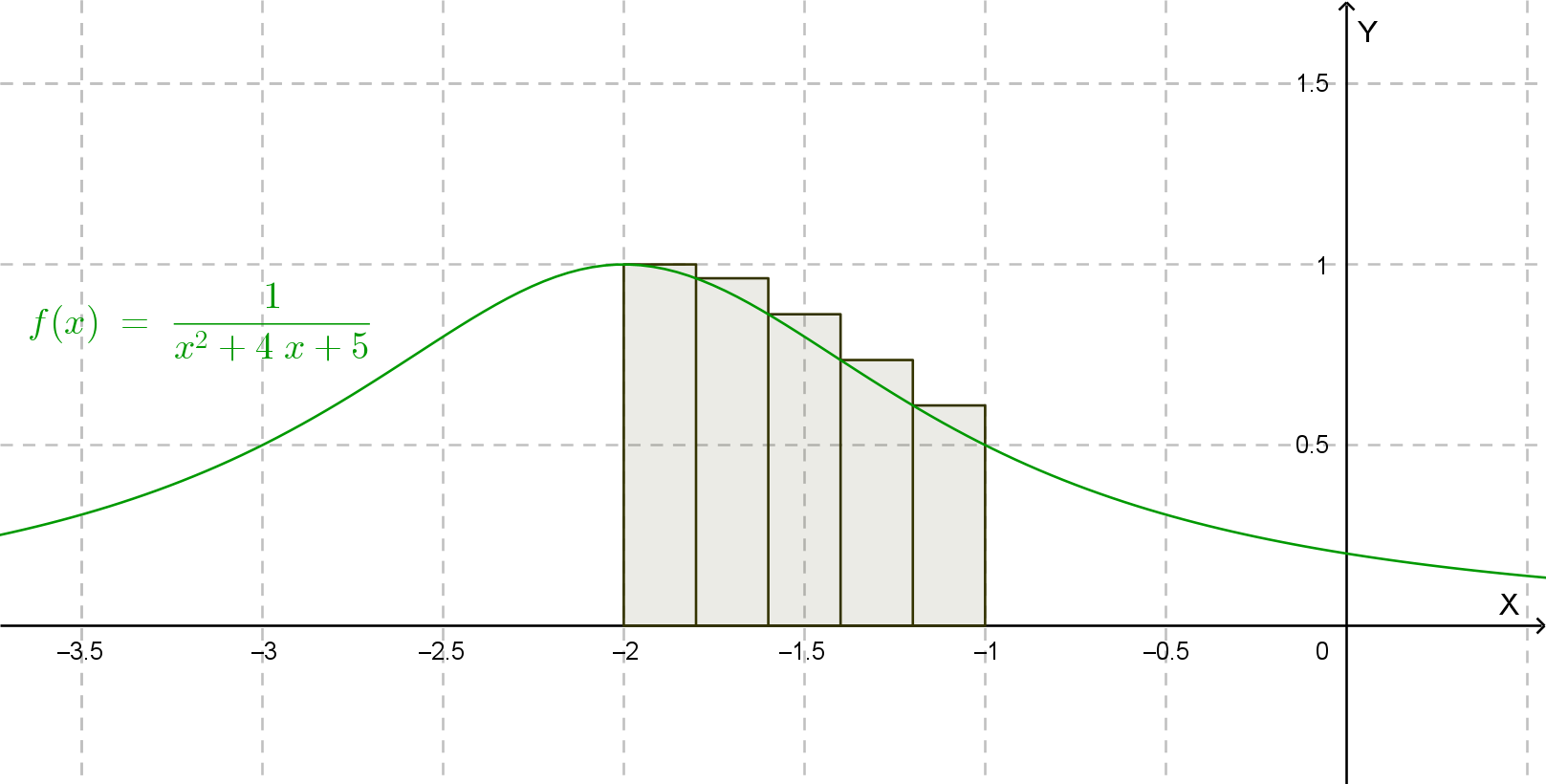 Valori: f(-2.0)=1, f(-1.8)≈0.9615,
f(-1.6)≈0.8621, f(-1.4)≈0.7353, f(-1.2)≈0.6098
Somma = 1 + 0.9615 + 0.8621 + 0.7353 + 0.6098 = 4.1687
R(c) = 0.2 × 4.1687 ≈ 0.8337
3. Media dei due metodi:
R = 0.8337 + 0.73372 ≈ 0.7837 ≈ 0.784
Valori: f(-2.0)=1, f(-1.8)≈0.9615,
f(-1.6)≈0.8621, f(-1.4)≈0.7353, f(-1.2)≈0.6098
Somma = 1 + 0.9615 + 0.8621 + 0.7353 + 0.6098 = 4.1687
R(c) = 0.2 × 4.1687 ≈ 0.8337
3. Media dei due metodi:
R = 0.8337 + 0.73372 ≈ 0.7837 ≈ 0.784
Mostriamo il grafico, anche se non richiesto:
![Grafico funzione √[(1-x)/(1+x)]](graphff.png) 1. Riscriviamo la funzione:
√1−x1+x = 1−x√1−x2
2. Separiamo l'integrale:
∫1√1−x2dx − ∫x√1−x2dx
3. Calcoliamo le primitive:
= arcsin(x) + √1−x2 +C
4. Valutiamo tra 0 e 1:
[arcsin(1) + 0] − [arcsin(0) + 1] = π2 − 1 ≈ 0.5708
1. Riscriviamo la funzione:
√1−x1+x = 1−x√1−x2
2. Separiamo l'integrale:
∫1√1−x2dx − ∫x√1−x2dx
3. Calcoliamo le primitive:
= arcsin(x) + √1−x2 +C
4. Valutiamo tra 0 e 1:
[arcsin(1) + 0] − [arcsin(0) + 1] = π2 − 1 ≈ 0.5708
Mostriamo il grafico, anche se non richiesto:
![Grafico funzione √[(1-x)/(1+x)]](graphfftrapezi.png) Parametri:
h = 1−05 = 0.2
x₀=0, x₁=0.2, x₂=0.4, x₃=0.6, x₄=0.8, x₅=1
Valori funzione:
f(0) = 1 f(0.2) ≈ 0.816 f(0.4) ≈ 0.655
f(0.6) ≈ 0.5 f(0.8) ≈ 0.333 f(1) = 0
Applicazione formula:
T₅ = 0.2 × [1+02 + 0.816 + 0.655 + 0.5 + 0.333]
= 0.2 × [0.5 + 2.304] = 0.2 × 2.804 ≈ 0.561
Parametri:
h = 1−05 = 0.2
x₀=0, x₁=0.2, x₂=0.4, x₃=0.6, x₄=0.8, x₅=1
Valori funzione:
f(0) = 1 f(0.2) ≈ 0.816 f(0.4) ≈ 0.655
f(0.6) ≈ 0.5 f(0.8) ≈ 0.333 f(1) = 0
Applicazione formula:
T₅ = 0.2 × [1+02 + 0.816 + 0.655 + 0.5 + 0.333]
= 0.2 × [0.5 + 2.304] = 0.2 × 2.804 ≈ 0.561
1. Rettangoli inscritti.
Mostriamo il grafico, anche se non richiesto:
![Grafico funzione √[(1-x)/(1+x)]](graphffrettangoliinscritti.png) Parametri:
h = 1−05 = 0.2
x₀=0, x₁=0.2, x₂=0.4, x₃=0.6, x₄=0.8, x₅=1
Valori funzione:
f(0) = 1 f(0.2) ≈ 0.816 f(0.4) ≈ 0.655
f(0.6) ≈ 0.5 f(0.8) ≈ 0.333 f(1) = 0
Somma = 0.816 + 0.655 + 0.5 + 0.333 + 0 = 2.304
R(i) = 0.2 × 2.304 ≈ 0.4608
2. Rettangoli circoscritti.
Mostriamo il grafico, anche se non richiesto:
Parametri:
h = 1−05 = 0.2
x₀=0, x₁=0.2, x₂=0.4, x₃=0.6, x₄=0.8, x₅=1
Valori funzione:
f(0) = 1 f(0.2) ≈ 0.816 f(0.4) ≈ 0.655
f(0.6) ≈ 0.5 f(0.8) ≈ 0.333 f(1) = 0
Somma = 0.816 + 0.655 + 0.5 + 0.333 + 0 = 2.304
R(i) = 0.2 × 2.304 ≈ 0.4608
2. Rettangoli circoscritti.
Mostriamo il grafico, anche se non richiesto:
![Grafico funzione √[(1-x)/(1+x)]](graphffrettangolicircoscritti.png) Somma = 1 + 0.816 + 0.655 + 0.5 + 0.333 = 3.304
R(c)= 0.2 × 3.304 ≈ 0.6608
3. Media dei due metodi:
R = 0.6608 + 0.46082 ≈ 0.5608 ≈ 0.561
Somma = 1 + 0.816 + 0.655 + 0.5 + 0.333 = 3.304
R(c)= 0.2 × 3.304 ≈ 0.6608
3. Media dei due metodi:
R = 0.6608 + 0.46082 ≈ 0.5608 ≈ 0.561