Questionario sulla Monotonia di una Funzione e Massimi/Minimi
Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.


Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.
Studiare la monotonia della funzione e determinare eventuali punti di massimo e minimo relativi:
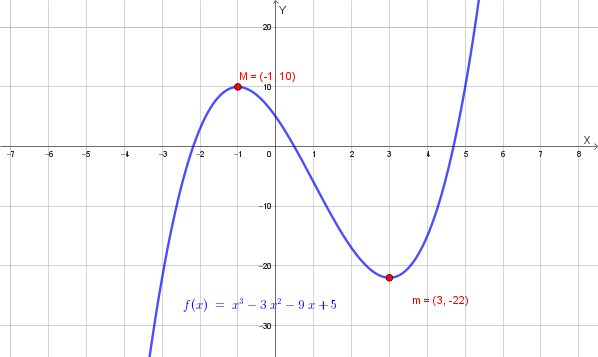
\[f(x) = x^3 - 3x^2 - 9x + 5\]Soluzione quesito 1:
Passo 1: Calcolo della derivata prima
Per studiare la monotonia, calcoliamo la derivata prima:
\[f'(x) = 3x^2 - 6x - 9 = 3(x^2 - 2x - 3) = 3(x-3)(x+1)\]Passo 2: Studio del segno di \(f'(x)\)
I punti critici sono \(x = -1\) e \(x = 3\). Studiamo il segno:
| Intervallo | \(x+1\) | \(x-3\) | \(f'(x)\) |
|---|---|---|---|
| \(x < -1\) | − | − | + |
| \(-1 < x < 3\) | + | − | − |
| \(x > 3\) | + | + | + |
Passo 3: Conclusioni
Grafico qualitativo della funzione:
Determinare gli intervalli di monotonia e i punti di estremo della funzione:
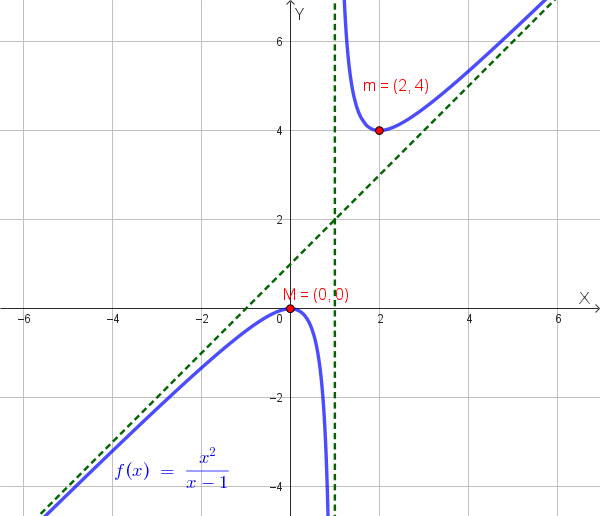
\[f(x) = \frac{x^2}{x-1}\]Soluzione quesito 2:
Dominio: \(D = \mathbb{R} \setminus \{1\}\) (la funzione ha un asintoto verticale in \(x=1\))
Passo 1: Calcolo della derivata prima
Usando la regola del quoziente:
\[f'(x) = \frac{2x(x-1) - x^2 \cdot 1}{(x-1)^2} = \frac{2x^2 - 2x - x^2}{(x-1)^2} = \frac{x^2 - 2x}{(x-1)^2} = \frac{x(x-2)}{(x-1)^2}\]Passo 2: Studio del segno di \(f'(x)\)
Punti critici: \(x = 0\) e \(x = 2\) (numeratore), \(x = 1\) (non nel dominio)
| Intervallo | \(x\) | \(x-2\) | \((x-1)^2\) | \(f'(x)\) |
|---|---|---|---|---|
| \(x < 0\) | − | − | + | + |
| \(0 < x < 1\) | + | − | + | − |
| \(1 < x < 2\) | + | − | + | − |
| \(x > 2\) | + | + | + | + |
Passo 3: Conclusioni
Grafico qualitativo della funzione:
Studiare la monotonia della funzione e trovare massimi e minimi assoluti nell'intervallo \([0, 3]\):
\[f(x) = x^3 - 6x^2 + 9x + 1\]Soluzione quesito 3:
Passo 1: Calcolo della derivata prima
\[f'(x) = 3x^2 - 12x + 9 = 3(x^2 - 4x + 3) = 3(x-1)(x-3)\]Passo 2: Studio del segno e punti critici in \([0,3]\)
Punti critici nell'intervallo: \(x = 1\) e \(x = 3\)
Passo 3: Calcolo dei valori agli estremi e nei punti critici
Passo 4: Conclusioni
Grafico qualitativo della funzione:
![Grafico qualitativo della funzione f(x) = x³ - 6x² + 9x + 1 nell'intervallo [0,3]](quesito3.png)
Determinare la monotonia della funzione:
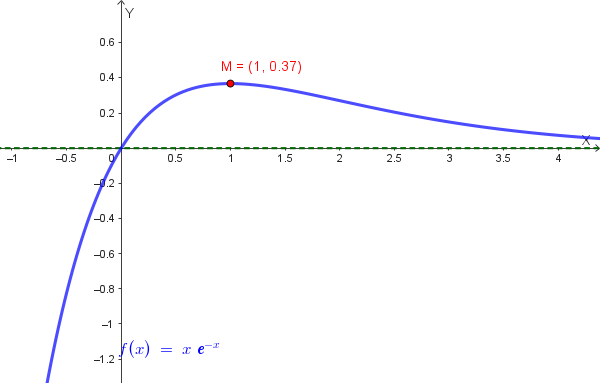
\[f(x) = x e^{-x}\]Soluzione quesito 4:
Passo 1: Calcolo della derivata prima
Usando la regola del prodotto:
\[f'(x) = 1 \cdot e^{-x} + x \cdot (-e^{-x}) = e^{-x}(1 - x)\]Passo 2: Studio del segno di \(f'(x)\)
Poiché \(e^{-x} > 0\) per ogni \(x\), il segno di \(f'(x)\) dipende solo da \((1-x)\):
Passo 3: Conclusioni
Grafico qualitativo della funzione:
Studiare la monotonia e determinare massimi e minimi della funzione:
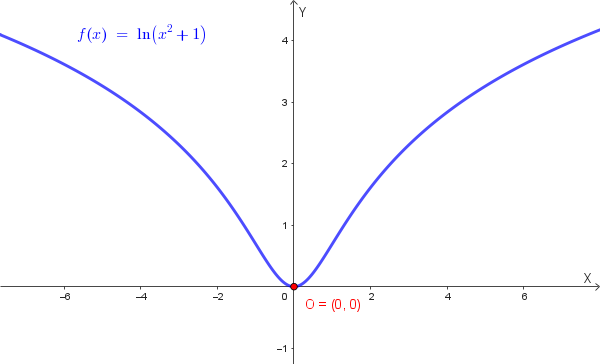
\[f(x) = \ln(x^2 + 1)\]Soluzione quesito 5:
Dominio: \(D = \mathbb{R}\) (poiché \(x^2 + 1 > 0\) per ogni \(x\))
Passo 1: Calcolo della derivata prima
Usando la regola di derivazione del logaritmo composto:
\[f'(x) = \frac{1}{x^2 + 1} \cdot 2x = \frac{2x}{x^2 + 1}\]Passo 2: Studio del segno di \(f'(x)\)
Il denominatore \(x^2 + 1\) è sempre positivo, quindi il segno dipende solo dal numeratore \(2x\):
Passo 3: Conclusioni
Nota: Non esiste massimo assoluto. Minimo assoluto \(O=(0,0) \)
Grafico qualitativo della funzione:
Determinare gli intervalli di monotonia della funzione:
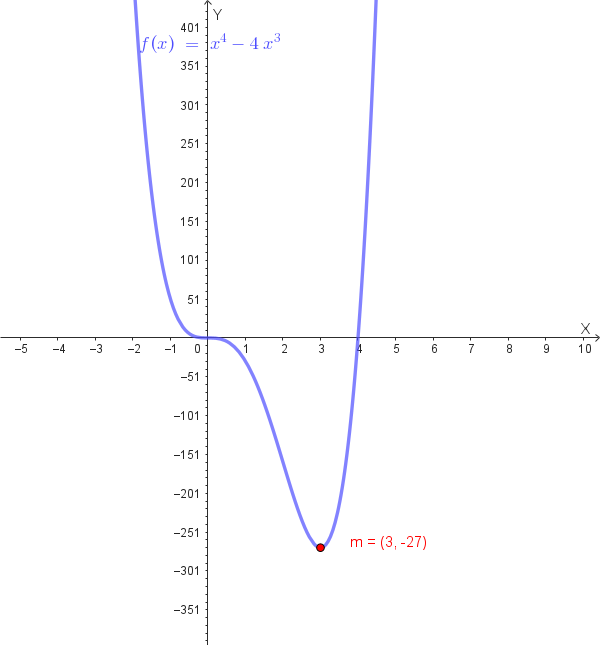
\[f(x) = x^4 - 4x^3\]Soluzione quesito 6:
Passo 1: Calcolo della derivata prima
\[f'(x) = 4x^3 - 12x^2 = 4x^2(x - 3)\]Passo 2: Studio del segno di \(f'(x)\)
Punti critici: \(x = 0\) (con molteplicità 2) e \(x = 3\)
Il fattore \(4x^2\) è sempre non negativo (positivo per \(x \neq 0\)), quindi il segno dipende da \((x-3)\):
Passo 3: Analisi del punto \(x = 0\)
In \(x = 0\) la derivata si annulla, ma la funzione è decrescente sia prima che dopo. Quindi \(x = 0\) è un punto di flesso a tangente orizzontale, non un punto di estremo.
Passo 4: Calcolo dei valori
Conclusioni:
Grafico qualitativo della funzione:
Trovare massimi e minimi assoluti della funzione nell'intervallo \([0, 2\pi]\):
\[f(x) = \sin(x) + \cos(x)\]Soluzione quesito 7:
Passo 1: Calcolo della derivata prima
\[f'(x) = \cos(x) - \sin(x)\]Passo 2: Ricerca dei punti critici in \([0, 2\pi]\)
Risolviamo \(f'(x) = 0\):
\[\cos(x) - \sin(x) = 0 \implies \cos(x) = \sin(x) \implies \tan(x) = 1\]Le soluzioni in \([0, 2\pi]\) sono: \(x = \frac{\pi}{4}\) e \(x = \frac{5\pi}{4}\)
Passo 3: Calcolo dei valori nei punti critici e agli estremi
Conclusioni:
Grafico qualitativo della funzione:
![Grafico qualitativo della funzione f(x) = sin(x) + cos(x) nell'intervallo [0,2π]](quesito7.png)
Studiare la monotonia della funzione:
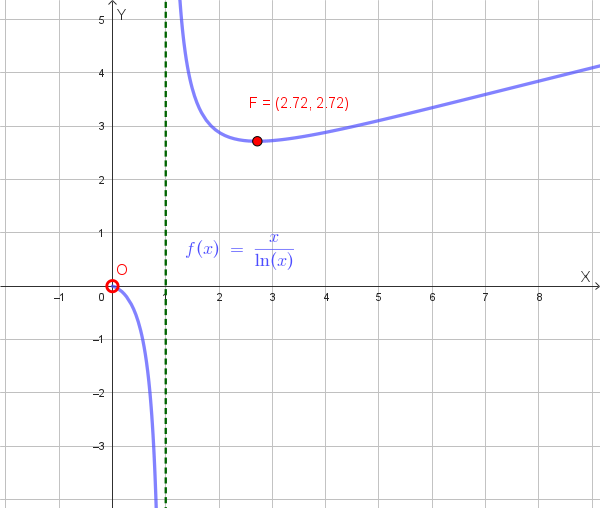
\[f(x) = \frac{x}{\ln(x)}\]Soluzione quesito 8:
Dominio: \(D = (0, 1) \cup (1, +\infty)\) (dobbiamo escludere \(x \leq 0\) per il logaritmo e \(x = 1\) perché \(\ln(1) = 0\))
Passo 1: Calcolo della derivata prima
Usando la regola del quoziente:
\[f'(x) = \frac{1 \cdot \ln(x) - x \cdot \frac{1}{x}}{[\ln(x)]^2} = \frac{\ln(x) - 1}{[\ln(x)]^2}\]Passo 2: Studio del segno di \(f'(x)\)
Il denominatore \([\ln(x)]^2\) è sempre positivo (quando definito), quindi il segno dipende dal numeratore:
Passo 3: Conclusioni
Grafico qualitativo della funzione:
Determinare il valore del parametro \(a > 0\) affinché la funzione
\[f(x) = x^3 - 3ax + 2\]abbia un minimo relativo in \(x = 2\).
Soluzione quesito 9:
Passo 1: Condizione necessaria per l'estremo
Affinché \(x = 2\) sia punto di estremo, deve essere \(f'(2) = 0\).
Calcoliamo la derivata:
\[f'(x) = 3x^2 - 3a\]Imponiamo \(f'(2) = 0\):
\[f'(2) = 3(2)^2 - 3a = 12 - 3a = 0\] \[3a = 12 \implies a = 4\]Passo 2: Verifica che sia un minimo
Con \(a = 4\), abbiamo \(f'(x) = 3x^2 - 12 = 3(x^2 - 4) = 3(x-2)(x+2)\)
Studio del segno:
La funzione passa da decrescente a crescente in \(x = 2\), quindi è effettivamente un punto di minimo.
Alternativamente, usando la derivata seconda:
\[f''(x) = 6x\] \[f''(2) = 12 > 0\]Poiché \(f''(2) > 0\), il punto è un minimo.
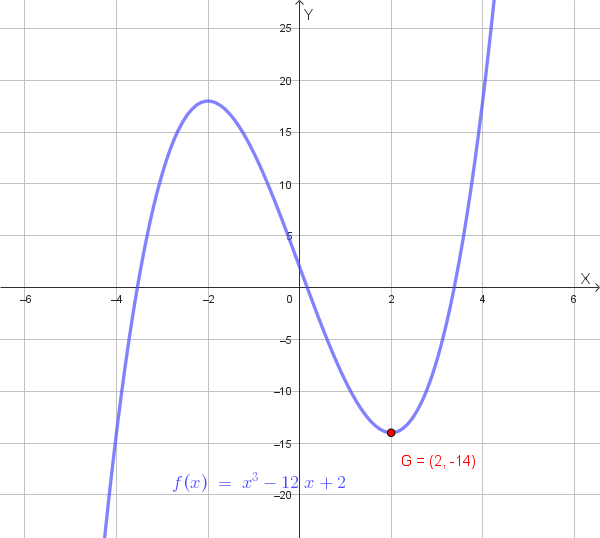
Risposta: \(a = 4\)
Grafico qualitativo della funzione con \(a = 4\):
Animazione:
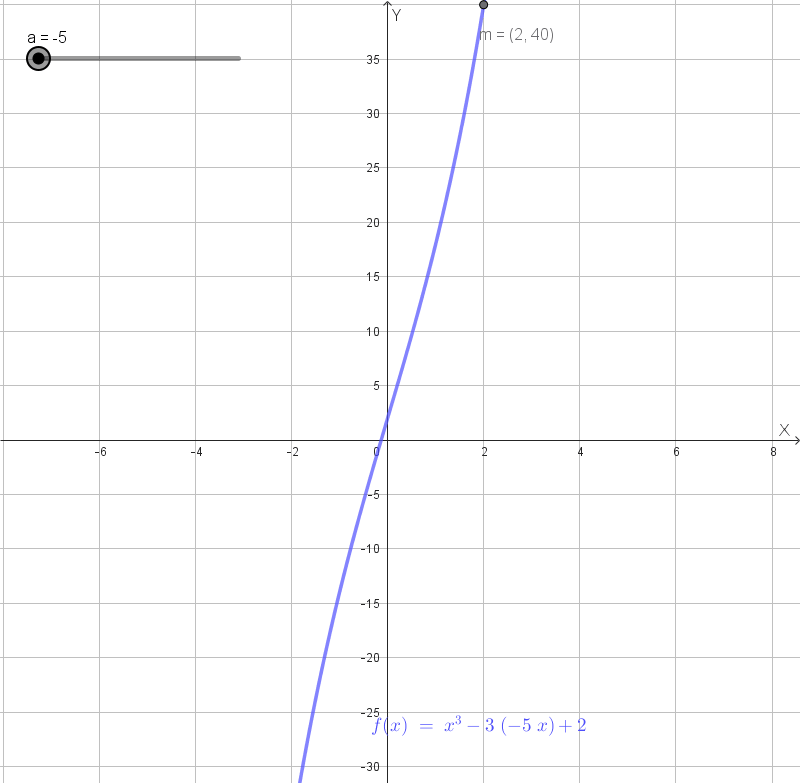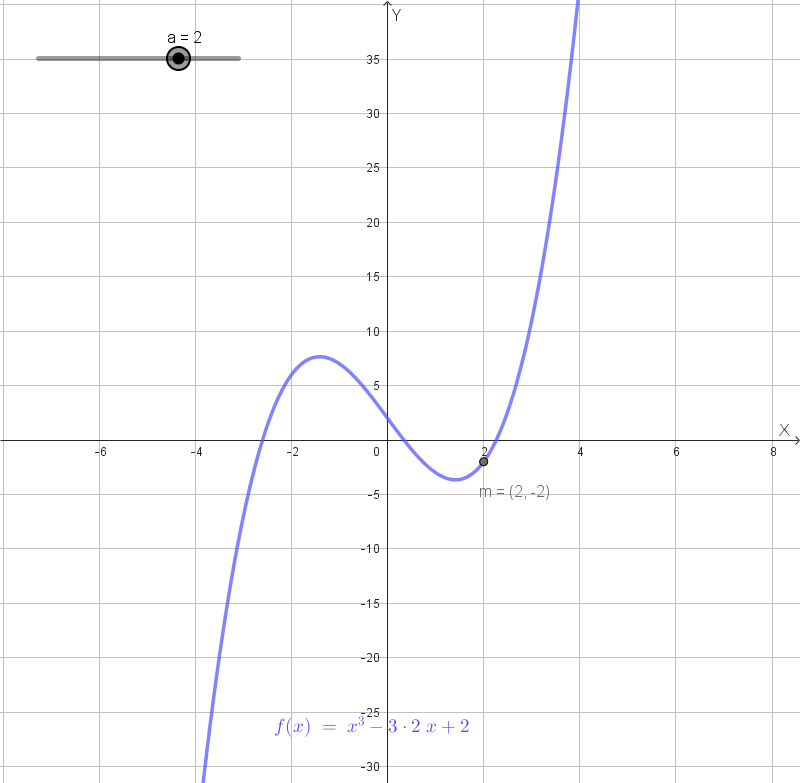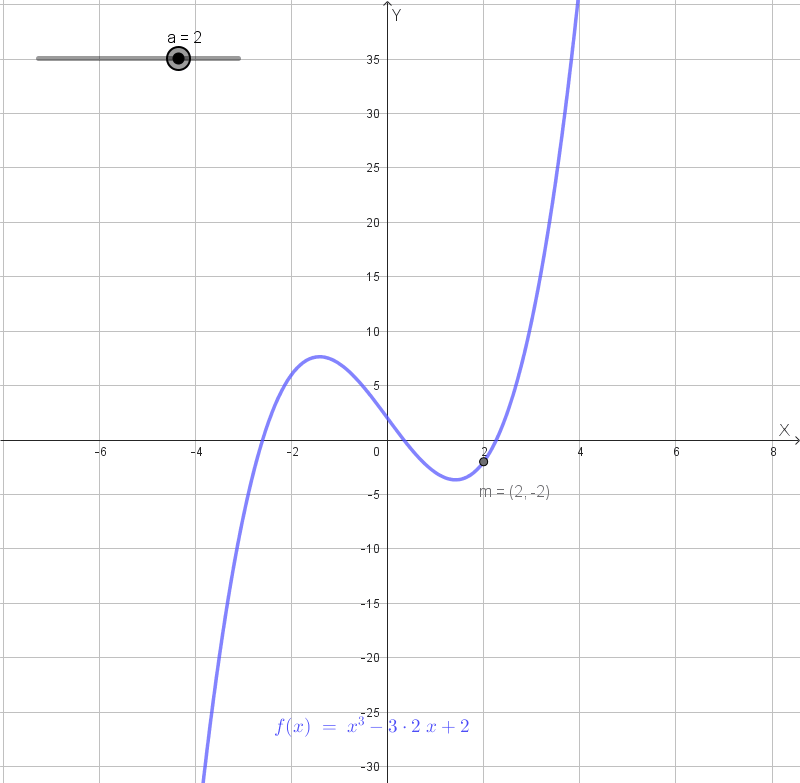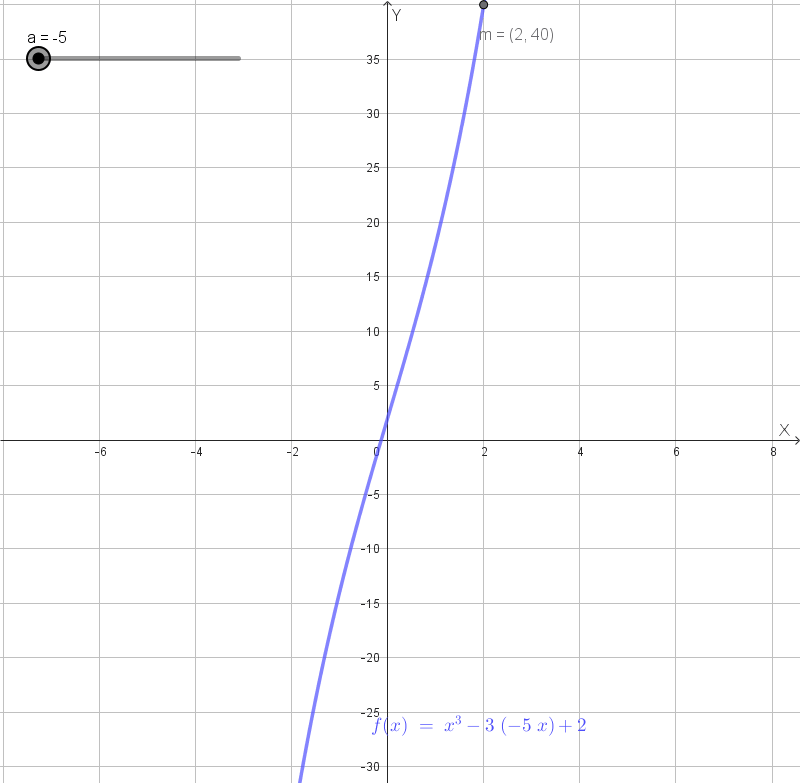
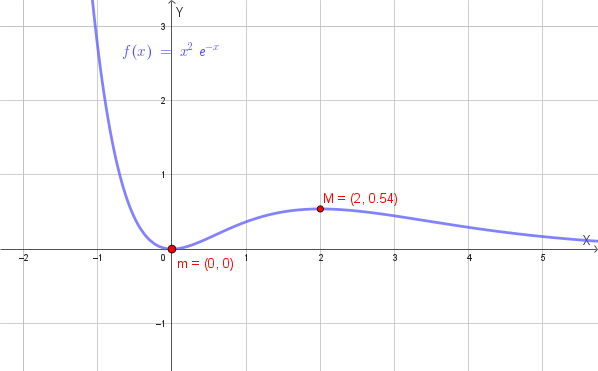
Data la funzione \(f(x) = x^2 e^{-x}\), determinare:
Soluzione quesito 10:
Dominio: \(D = \mathbb{R}\)
a) Calcolo della derivata prima
Usando la regola del prodotto:
\[f'(x) = 2x \cdot e^{-x} + x^2 \cdot (-e^{-x}) = e^{-x}(2x - x^2) = x e^{-x}(2 - x)\]Studio del segno di \(f'(x)\)
Poiché \(e^{-x} > 0\) per ogni \(x\), il segno dipende da \(x(2-x)\):
| Intervallo | \(x\) | \(2-x\) | \(f'(x)\) | Monotonia |
|---|---|---|---|---|
| \(x < 0\) | − | + | − | Decrescente |
| \(0 < x < 2\) | + | + | + | Crescente |
| \(x > 2\) | + | − | − | Decrescente |
b) Punti di estremo
c) Comportamento agli estremi
Riepilogo:
Grafico qualitativo della funzione: