Risolvi da solo i singoli problemi e controlla la soluzione premendo il tasto corrispondente.
Problema 1
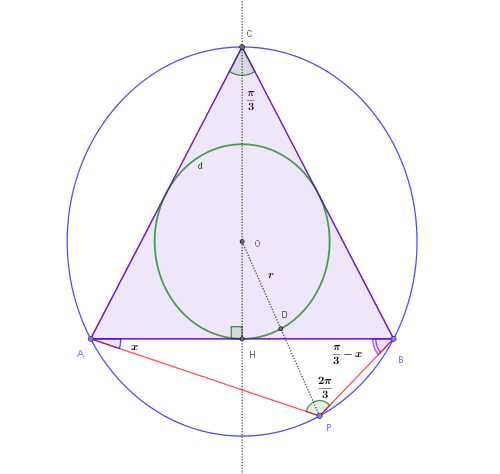
Considera un triangolo equilatero \(ABC\) di lato \(AB = 6\). Indichiamo con \(R\) il raggio della circonferenza circoscritta e con \(r\) il raggio della circonferenza inscritta; sia \(O\) il centro comune.
Sia \(P\) un punto mobile appartenente al minore degli archi \(AB\) della circonferenza circoscritta (cioè l’arco che non contiene \(C\)). Indichiamo con \[ x = \widehat{PAB} \] l’angolo in \(A\) compreso tra il lato \(AB\) e il segmento \(AP\).
a) Calcola i raggi \(R\) e \(r\) (circoscritta e inscritta) del triangolo equilatero. Stabilisci inoltre se la distanza di \(P\) dalla circonferenza inscritta dipende dalla posizione di \(P\) sulla circonferenza circoscritta.
b) Esprimi in funzione di \(x\) la lunghezza \(AP\) e scrivi la funzione \[ f(x) = \mathrm{Area}(APB). \]
c) Studia la funzione \(f(x)\) tendendo conto dei limiti geometrici di \(x\) e rappresentala graficamente .
La figura del Problema è la seguente
Soluzione Problema 1:
a) Calcolo di \(R\), \(r\) e distanza del punto \(P\) dalla circonferenza inscritta
Per un triangolo equilatero di lato \(l\) valgono le formule note:
\[ R = \frac{l}{\sqrt{3}}, \qquad r = \frac{l}{2}\frac{\sqrt{3}}{3}. \]Con \(l = 6\):
\[ R = 2\sqrt{3}, \qquad r = \sqrt{3}. \]Poiché il punto \(P\) giace sulla circonferenza circoscritta, la sua distanza dal centro è:
\[ OP = R. \]La distanza radiale di \(P\) dalla circonferenza inscritta (a centro coincidente) è:
\[ d(P) = OP - r = R - r = 2\sqrt{3} - \sqrt{3} = \sqrt{3}. \]Conclusione: la distanza di \(P\) dalla circonferenza inscritta non dipende dalla posizione di \(P\) sulla circonferenza circoscritta: è costante e vale \( \sqrt{3}\).
b) Espressione di \(AP\) e area del triangolo \(APB\)
L’arco minore \(AB\) corrisponde a un angolo al centro di:
\[ \widehat{AOB} = \frac{2\pi}{3}. \]L’angolo \(\widehat{APB}\) è supplementare dell'angolo in \(C\), quindi:
\[ \widehat{APB} = \frac{2\pi}{3} \]Risulta quindi:
\[ \widehat{ABP} = \pi -x-\frac{2\pi}{3}=\frac{\pi}{3}-x \]Per il Teorema della corda risulta:
\[ AP = 2R\sin\left(\frac{\pi}{3} - x\right). \]Sostituendo \(R = 2\sqrt{3}\):
\[ AP = 4\sqrt{3}\,\sin\left(\frac{\pi}{3} - x\right). \]L’area del triangolo \(APB\), usando una nota formula goniometrica, è:
\[ f(x) = \mathrm{Area}(APB) = \frac{1}{2}\,AB \cdot AP \cdot \sin x = 3 \cdot AP \cdot \sin x. \]Sostituendo \(AP\):
\[ \boxed{f(x) = 12\sqrt{3}\,\sin x \,\sin\left(\frac{\pi}{3} - x\right)}. \]c) Limiti geometrici, studio della funzione e grafico qualitativo
Limiti geometrici dell’angolo \(x =\widehat{APB}\)
- Se \(P = B\), allora \(x = \widehat{BAB} = 0\). In questo caso il triangolo \(APB\) è degenere e l’area vale 0.
- Se \(P\) coincide con \(A\), il segmento \(AP\) diventa tangente alla circonferenza circoscritta. L’angolo tra la tangente in \(A\) e la corda \(AB\) (cioè l’angolo limite \( \widehat{PAB} \) è uguale all’angolo inscritto che insiste sul minore arco \(AB\), cioè \( \widehat{ACB} = \pi/3\).
Dunque i limiti geometrici sono:
\[ \boxed{0 \le x \le \frac{\pi}{3}}. \]Studio della funzione \(f(x)\)
La funzione è \[ f(x) = 12\sqrt{3}\,\sin x\,\sin\left(\frac{\pi}{3}-x\right), \qquad 0 \le x \le \frac{\pi}{3}. \]
1) Zeri della funzione
Un prodotto è nullo quando almeno uno dei fattori è nullo. Valutiamo:
- \(\sin x = 0 \implies x = 0\)
- \(\sin(\tfrac{\pi}{3}-x)=0 \implies \tfrac{\pi}{3}-x=0 \implies x=\tfrac{\pi}{3}\)
Quindi:
\[ f(0)=0, \qquad f\left(\frac{\pi}{3}\right)=0. \]2) Segno della funzione
Sull’intervallo \((0,\tfrac{\pi}{3})\) valgono:
- \(\sin x > 0\)
- \(\sin(\tfrac{\pi}{3}-x) > 0\)
Quindi:
\(f(x) > 0 \quad \text{per } 0 < x < \frac{\pi}{3}\)
3) Derivata prima e monotonia
Partiamo dalla forma sviluppata di \(f(x)\) (ottenuta sviluppando il seno della differenza):
\[ f(x)=12\sqrt{3}\,\sin x\left(\frac{\sqrt{3}}{2}\cos x - \frac{1}{2}\sin x\right) =18\sin x\cos x - 6\sqrt{3}\sin^2 x. \]Deriviamo termine per termine:
\[ \frac{d}{dx}\big(18\sin x\cos x\big)=18(\cos^2 x - \sin^2 x)=18\cos 2x, \] \[ \frac{d}{dx}\big(-6\sqrt{3}\sin^2 x\big)=-12\sqrt{3}\sin x\cos x=-6\sqrt{3}\sin 2x. \]Quindi la derivata prima è
\[ \boxed{\,f'(x)=18\cos 2x - 6\sqrt{3}\sin 2x\, }. \]Poniamo \(f'(x)=0\):
\[ 18\cos 2x - 6\sqrt{3}\sin 2x = 0 \quad\Longrightarrow\quad 3\cos 2x - \sqrt{3}\sin 2x = 0. \]Da ciò otteniamo
\[ \tan 2x = \frac{3}{\sqrt{3}} = \sqrt{3}. \]Le soluzioni sono
\[ 2x = \frac{\pi}{3} + k\pi \quad\Longrightarrow\quad x = \frac{\pi}{6} + \frac{k\pi}{2},\qquad k\in\mathbb{Z}. \]Nell'intervallo geometrico \(0 \le x \le \frac{\pi}{3}\) l'unica soluzione utile è
\[ \boxed{x=\frac{\pi}{6}}. \]Studio del segno di \(f'\):
Trasformiamo l’espressione della derivata prima in una forma più compatta, utile per studiare il segno. Partiamo dalla forma sviluppata:
\[ f'(x) = 18 \cos(2x) - 6\sqrt{3}\sin(2x). \]Raccogliamo a fattore comune \(12\sqrt{3}\) in modo da far comparire i coefficienti \(\frac{\sqrt{3}}{2}\) e \(\frac{1}{2}\), che sono i valori noti del seno e coseno di \(\frac{\pi}{3}\):
\[ f'(x) = 12\sqrt{3}\left(\frac{18}{12\sqrt{3}} \cos(2x) - \frac{6\sqrt{3}}{12\sqrt{3}} \sin(2x)\right) \]Semplificando i coefficienti (\(\frac{18}{12\sqrt{3}} = \frac{3}{2\sqrt{3}} = \frac{3\sqrt{3}}{6} = \frac{\sqrt{3}}{2}\) e \(\frac{6\sqrt{3}}{12\sqrt{3}} = \frac{1}{2}\)), otteniamo il primo passaggio intermedio:
\[ f'(x) = 12\sqrt{3}\left(\frac{\sqrt{3}}{2} \cos(2x) - \frac{1}{2} \sin(2x)\right). \]Riconosciamo l'espressione tra parentesi come la **formula di sottrazione del seno**, sapendo che \(\sin\left(\frac{\pi}{3}\right) = \frac{\sqrt{3}}{2}\) e \(\cos\left(\frac{\pi}{3}\right) = \frac{1}{2}\):
\[ \sin(a-b)=\sin a\cos b - \cos a\sin b. \]Sostituendo \(a = \frac{\pi}{3}\) e \(b = 2x\):
\[ f'(x) = 12 \sqrt{3}\sin \left(\frac{\pi}{3}-2x\right). \]Infine, applichiamo la **formula dell’argomento negativo del seno**, \(\sin(-z) = -\sin(z)\), per invertire l'ordine dei termini nell'argomento e ottenere la forma finale:
\[ \sin\!\left(\tfrac{\pi}{3}-2x\right) = \sin\!\left[-(2x-\tfrac{\pi}{3})\right] = -\sin\!\left(2x-\tfrac{\pi}{3}\right). \]Sostituendo, otteniamo la conclusione:
\[ f'(x) = 12\sqrt{3}\left[-\sin\left(2x-\frac{\pi}{3}\right)\right] = -12\sqrt{3}\,\sin\!\left(2x-\frac{\pi}{3}\right). \]Conclusione: la derivata può essere scritta nella forma compatta:
\[ f'(x) = -12\sqrt{3}\,\sin\!\left(2x-\frac{\pi}{3}\right). \]Questa forma è molto utile perché il segno di \(f'\) dipende direttamente dal segno del seno di \(2x-\tfrac{\pi}{3}\).
Studio del Segno di \(f'(x)\) e Punti Estremanti 🧐
La derivata prima è stata determinata nella forma compatta:
\[ f'(x) = -12\sqrt{3}\,\sin\!\left(2x-\frac{\pi}{3}\right). \]Dobbiamo verificare il segno di \(f'(x)\) nell'intervallo di studio \(0 \le x \le \frac{\pi}{3}\).
Poiché il fattore costante \(-12\sqrt{3}\) è negativo, il segno di \(f'(x)\) è determinato dal segno **opposto** del termine \(\sin\left(2x-\frac{\pi}{3}\right)\).
1. Punti Critici
I punti critici si trovano dove \(f'(x) = 0\), cioè quando \(\sin\left(2x-\frac{\pi}{3}\right) = 0\).
Nell'intervallo \(0 \le x \le \frac{\pi}{3}\), l'argomento \(y = 2x - \frac{\pi}{3}\) varia in \(\left[-\frac{\pi}{3}, \frac{\pi}{3}\right]\). L'unico punto in cui il seno è nullo in questo intervallo è \(y=0\):
\[ 2x - \frac{\pi}{3} = 0 \quad \Rightarrow \quad 2x = \frac{\pi}{3} \quad \Rightarrow \quad x = \frac{\pi}{6}. \]2. Studio del Segno
Verifichiamo ora il segno di \(f'(x)\):
- Per \(0 < x < \frac{\pi}{6}\): l'argomento \(2x - \frac{\pi}{3}\) è nell'intervallo \(\left(-\frac{\pi}{3}, 0\right)\), dove il seno è **negativo** (\(\sin(\dots) < 0\)). Di conseguenza, \(f'(x) = -12\sqrt{3} \cdot (\text{negativo}) > 0\). Quindi la funzione è **crescente** in questo intervallo.
- Per \(\frac{\pi}{6} < x < \frac{\pi}{3}\): l'argomento \(2x - \frac{\pi}{3}\) è nell'intervallo \(\left(0, \frac{\pi}{3}\right)\), dove il seno è **positivo** (\(\sin(\dots) > 0\)). Di conseguenza, \(f'(x) = -12\sqrt{3} \cdot (\text{positivo}) < 0\). Quindi la funzione è **decrescente** nell’intervallo successivo.
3) Ricerca di Massimi e Minimi
Il cambiamento di monotonia (crescente \(\rightarrow\) decrescente) in \(x=\tfrac{\pi}{6}\) indica la presenza di un **Massimo Relativo**.
Calcoliamo i valori della funzione \(f(x)\) nei punti estremanti.
Valore nel Massimo Assoluto (\(x=\frac{\pi}{6}\)):
Dal cambiamento di monotonia, \(x=\tfrac{\pi}{6}\) è un massimo assoluto nell'intervallo. Calcoliamo il valore massimo usando la forma originaria (come da tua richiesta):
\[ f\!\left(\tfrac{\pi}{6}\right) =12\sqrt{3}\,\sin\!\left(\tfrac{\pi}{6}\right)\sin\!\left(\tfrac{\pi}{3}-\tfrac{\pi}{6}\right) =12\sqrt{3}\,\sin\!\left(\tfrac{\pi}{6}\right)\sin\!\left(\tfrac{\pi}{6}\right) =12\sqrt{3}\cdot\frac{1}{2}\cdot\frac{1}{2} = 12\sqrt{3}\cdot\frac{1}{4}=3\sqrt{3}. \] \[ \boxed{f_{\max}=3\sqrt{3}\quad\text{in }x=\tfrac{\pi}{6}.} \]Valori nei Minimi (Estremi dell'Intervallo):
\[ f(0) = 12\sqrt{3}\,\sin(0)\sin(\tfrac{\pi}{3}-0) = 0. \]
\[ f\left(\frac{\pi}{3}\right) = 12\sqrt{3}\,\sin\left(\frac{\pi}{3}\right)\sin\left(\frac{\pi}{3}-\frac{\pi}{3}\right) = 12\sqrt{3}\,\sin\left(\frac{\pi}{3}\right)\sin(0) = 0. \]
\[ \boxed{f_{\min}=0\quad\text{in }x=0\text{ e }x=\tfrac{\pi}{3}.} \]5) Simmetria
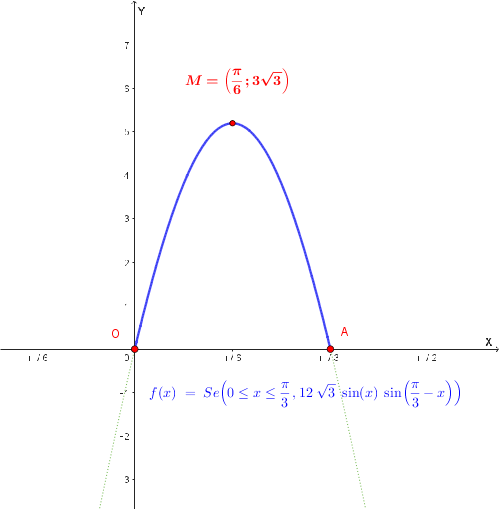
Notiamo che la funzione è simmetrica rispetto al punto centrale dell’intervallo \(x=\tfrac{\pi}{6}\).
Questo è confermato dalla figura del problema, in cui si osserva che l'area del triangolo assume lo stesso valore per i punti \(P\) simmetrici rispetto alla retta \(AH\).
Conclusione: la funzione
\[ f(x) = 12\sqrt{3}\,\sin x\,\sin\left(\frac{\pi}{3}-x\right) \]ha grafico “a cupola”: parte da 0, cresce fino al massimo in \(x=\pi/6\), quindi decresce tornando a 0 in \(x=\pi/3\).
Grafico della funzione
Problema 2
Soluzione Problema 2: Studio Completo della Funzione \(g(t)\)
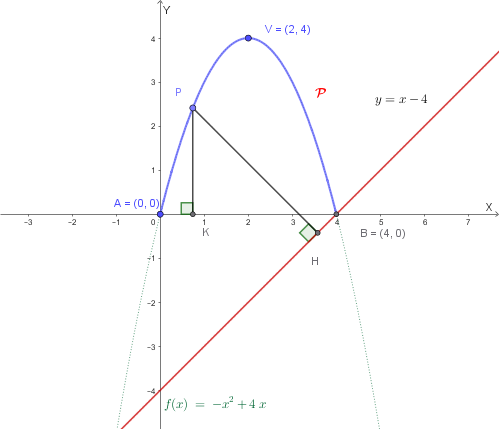
1. Studio della Parabola \(\mathcal{P}\) e Contesto Geometrico
La parabola ha equazione \(y = -x^2 + 4x\). Vertice \(V(2, 4)\) e intersezioni con l'asse \(x\) in \(A(0, 0)\) e \(B(4, 0)\). Il punto \(P\) si muove sull'arco dove \(t \in (0, 4)\) e la retta \(r\) è \(y=x-4\).
Figura rappresentativa del problema
Studiamo ora la funzione
\[ g(t)=\frac{\sqrt{2}\,\overline{PH}}{\overline{PK}-4}. \]
1. Coordinate del punto \(P\)
Poiché \(P\) ha ascissa \(t\) e appartiene alla parabola \(y=-t^{2}+4t\), abbiamo: \[ P(t,\,y_P)=(t,\,-t^{2}+4t). \]
2. Calcolo di \(\overline{PH}\)
La retta \(r\colon y=x-4\) si riscrive in forma implicita: \[ x-y-4=0. \] La distanza punto–retta è: \[ \overline{PH}=\frac{|t - y_P - 4|}{\sqrt{2}}. \] Sostituendo \(y_P=-t^{2}+4t\): \[ \sqrt{2}\,\overline{PH}=|\,t - (-t^{2}+4t) - 4\,|=|\,t^{2}-3t-4\,|. \]
3. Calcolo di \(\overline{PK}\)
La proiezione di \(P\) su \(x\) è \(K(t,0)\), dunque: \[ \overline{PK}=|y_P|=|-t^{2}+4t|. \]
4. Rimozione dei valori assoluti nell’intervallo \((0,4)\)
Per il denominatore
Osserviamo che \[ y_P=-t^{2}+4t > 0 \quad \Longleftrightarrow \quad -t^{2}+4t > 0, \] cioè \[ -t(t-4) > 0 \quad \Longleftrightarrow \quad t(t-4) < 0, \] che equivale a \[ 0 < t < 4. \] Dunque, nell’intervallo geometrico considerato: \[ |y_P|=y_P. \] Segue quindi: \[ \overline{PK}-4=(-t^{2}+4t)-4=-(t^{2}-4t+4)=-(t-2)^{2}\le 0. \]
Per il numeratore
Studiamo il segno del polinomio \[ t^{2}-3t-4. \] Risolviamo la disequazione \[ t^{2}-3t-4 \ge 0. \] Il trinomio si annulla per \[ t=\frac{3\pm\sqrt{9+16}}{2}=\frac{3\pm 5}{2} \quad\Longrightarrow\quad t=-1,\;4. \] Poiché il coefficiente di \(t^{2}\) è positivo, il segno è: \[ t^{2}-3t-4 \ge 0 \quad\text{per}\quad t\le -1\ \text{oppure}\ t\ge 4, \] e quindi \[ t^{2}-3t-4 < 0 \quad\text{per}\quad -1 < t < 4. \] Nel nostro intervallo geometrico \((0,4)\) abbiamo dunque: \[ |\,t^{2}-3t-4\,|=-(t^{2}-3t-4). \]
5. Espressione finale di \(g(t)\)
Usando le semplificazioni sopra otteniamo \[ g(t)=\frac{\sqrt{2}\,\overline{PH}}{\overline{PK}-4} =\frac{\;|\,t^2-3t-4\,|\;}{(-t^2+4t)-4} =\frac{-\big(t^2-3t-4\big)}{-\big(t^2-4t+4\big)} =\frac{t^2-3t-4}{t^2-4t+4}. \]
Conclusione: considerando i segni sul tratto geometrico \(t\in(0,4)\) si ottiene quindi la forma razionale
\(\displaystyle g(t)=\dfrac{t^{2}-3t-4}{t^{2}-4t+4}\)
2. Studio della Funzione \(g(t)\) (Dominio Naturale)
A) Dominio e Asintoti
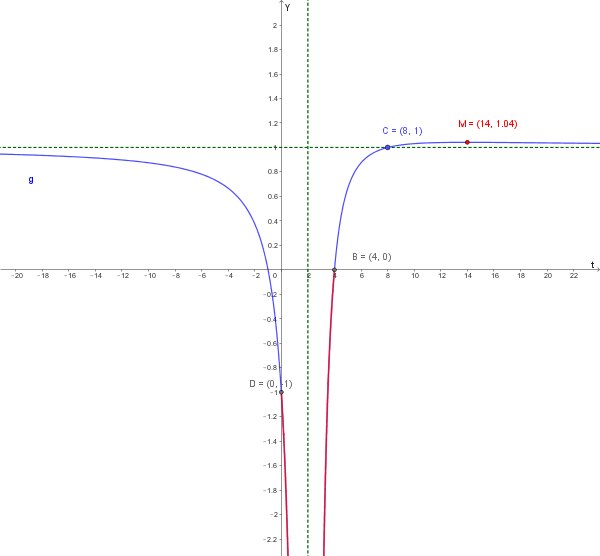
- Dominio: \(D = \mathbb{R} \setminus \{2\}\).
- Asintoto Verticale (\(t \to 2\)): \[ \lim_{t \to 2^\pm} g(t) = \frac{-6}{0^+} = -\infty. \]
- Asintoto Orizzontale (\(t \to \pm \infty\)): L'Asintoto Orizzontale è \(\mathbf{y = 1}\).
B) Intersezioni con gli Assi e con l'Asintoto
- Intersezione Asse \(t\) (Zeri): \(\mathbf{(-1, 0)}\) e \(\mathbf{(4, 0)}\).
- Intersezione Asse \(g(t)\): \(\mathbf{(0, -1)}\).
- Intersezione Asintoto (\(g(t)=1\)): Si ha per \(\mathbf{t = 8}\).
C) Studio del Segno
Vogliamo determinare i segni del numeratore e del denominatore di \[ g(t)=\frac{t^{2}-3t-4}{t^{2}-4t+4}, \] per ricavarne il segno di \(g(t)\).
1. Denominatore
Il denominatore è \[ t^{2}-4t+4=(t-2)^{2}\ge 0 \] e si annulla solo in \(t=2\). Quindi per ogni \(t\neq 2\) il denominatore è positivo.
2. Numeratore
Il numeratore factorizza: \[ t^{2}-3t-4=(t-4)(t+1). \] Gli zeri sono \(t=-1\) e \(t=4\). Poiché il coefficiente di \(t^{2}\) è positivo, il segno del numeratore è:
- positivo per \(t\le -1\),
- negativo per \(-1<t<4\),
- positivo per \(t\ge 4\).
3. Segno della funzione
Dal punto 1 sappiamo che il denominatore è positivo per ogni \(t\neq 2\), perciò il segno di \(g(t)\) coincide con il segno del numeratore. Riassumiamo in una tabella con gli intervalli critici (ordinati sulle linee reali):
| Intervallo | Segno numeratore | Segno denominatore | Segno di g(t) |
|---|---|---|---|
| \((-\infty,\,-1)\) | + | + | + |
| \((-1,\,2)\) | - | + | - |
| \(t=2\) (punto escluso) | - | 0 | non definita (asintoto verticale) |
| \((2,\,4)\) | - | + | - |
| \((4,\,+\infty)\) | + | + | + |
4. Osservazioni finali
- Gli zeri di \(g\) sono \(t=-1\) e \(t=4\) (dove cambia segno passando da + a - o da - a +).
- In \(t=2\) la funzione non è definita: poiché il numeratore in 2 è \(-6\) e il denominatore tende a \(0^+\), si ha un asintoto verticale con \(g(t)\to -\infty\) da entrambi i lati.
- Quindi, in sintesi:
- \(g(t)>0\) per \(t<-1\) e per \(t>4\),
- \(g(t)<0\) per \(-1<t<4\) (escludendo \(t=2\) dove la funzione non è definita).
3. Monotonia e Punti Estremali
Calcolo dettagliato della derivata \(g'(t)\)
La funzione è: \[ g(t)=\frac{N(t)}{D(t)}=\frac{t^{2}-3t-4}{t^{2}-4t+4}, \] dove: \[ N(t)=t^{2}-3t-4,\quad D(t)=t^{2}-4t+4. \]
Calcoliamo le derivate dei polinomi: \[ N'(t)=2t-3,\qquad D'(t)=2t-4. \]
Applicando la regola del quoziente: \[ g'(t)=\frac{N'(t)D(t)-N(t)D'(t)}{[D(t)]^{2}}. \]
Primo prodotto: \[ (2t-3)(t^{2}-4t+4)=2t^{3}-11t^{2}+20t-12. \]
Secondo prodotto: \[ (2t-4)(t^{2}-3t-4)=2t^{3}-10t^{2}+4t+16. \]
Sottrazione: \[ \big(2t^{3}-11t^{2}+20t-12\big)-\big(2t^{3}-10t^{2}+4t+16\big) =-t^{2}+16t-28. \]
Otteniamo quindi: \[ \boxed{g'(t)=\frac{-t^{2}+16t-28}{(t^{2}-4t+4)^{2}}},\quad t\ne 2. \]
Fattorizzazione
Risolviamo: \[ -t^{2}+16t-28=0 \Longleftrightarrow t^{2}-16t+28=0. \] Il discriminante è: \[ \Delta=256-112=144=\;12^{2}. \] Le radici sono: \[ t=\frac{16\pm 12}{2}=2,\;14. \] Dunque: \[ -t^{2}+16t-28 = -(t-2)(t-14). \]
Il denominatore: \[ (t^{2}-4t+4)^{2} = (t-2)^{4}. \]
Per \(t\ne 2\): \[ g'(t)=\frac{-(t-2)(t-14)}{(t-2)^{4}} =\frac{-(t-14)}{(t-2)^{3}}. \]
Studio del segno di \(g'(t)\)
Numeratore \( -(t-14) \):
- Se \(t < 14\): \((t-14) < 0\) ⇒ \(-(t-14)>0\).
- Se \(t > 14\): \((t-14) > 0\) ⇒ \(-(t-14)<0\).
Denominatore \((t-2)^{3}\) (mantiene il segno di \(t-2\)):
- Se \(t < 2\): \((t-2)^{3}<0\).
- Se \(t > 2\): \((t-2)^{3}>0\).
Tabella dei segni:
| Intervallo | Segno numeratore | Segno denominatore | Segno di g'(t) |
|---|---|---|---|
| \((-\infty,2)\) | + | - | - |
| \((2,14)\) | + | + | + |
| \((14,+\infty)\) | - | + | - |
Conclusioni sulla monotonia:
- Decrescente su \((-\infty,2)\)
- Crescente su \((2,14)\)
- Decrescente su \((14,+\infty)\)
La derivata si annulla in \(t=14\), quindi:
Massimo relativo in \(t=14\): \[ g(14)=\frac{25}{24}. \]
4. Conclusione (Tratto Geometrico \((0,4)\))
Nell’intervallo di interesse \((0,4)\):
- Decrescente da \(t=0\) (dove \(g(0)=-1\)) a \(t\to 2^{-}\) (con \(g(t)\to -\infty\)).
- Crescente da \(t\to 2^{+}\) (da \(-\infty\)) fino a \(t=4\), dove \(g(4)=0\).
Il grafico completo della funzione e il tratto geometrico evidenziato sono i seguenti:
Problema 4
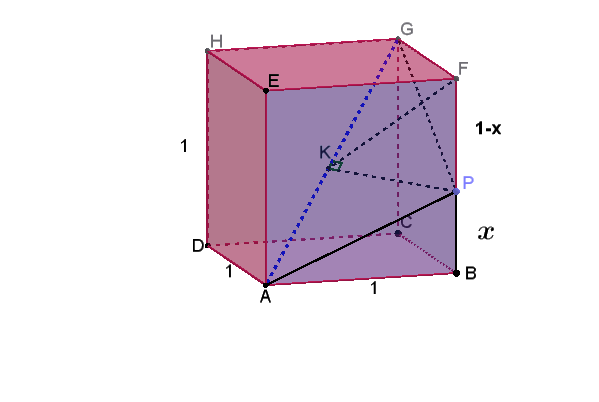
Nel cubo di vertici A, B, C, D, E, F, G, H le facce ABCD e EFGH sono opposte e i segmenti AE, BF, CG, DH sono spigoli. Gli spigoli del cubo hanno lunghezza unitaria.
Sullo spigolo BF prendere un punto P tale che BP = x.
a) Verificare che la distanza y di P dalla diagonale AG è espressa dalla seguente funzione:
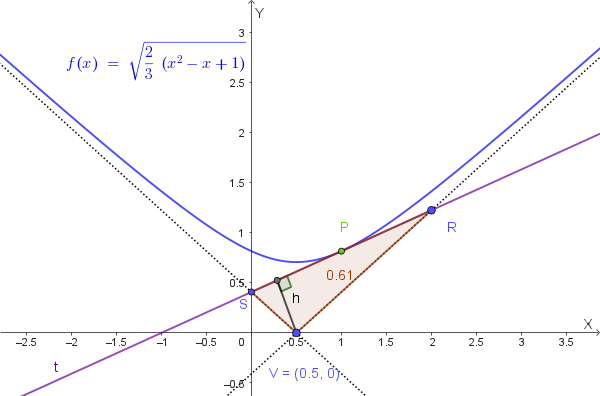
\[ y = \sqrt{\frac{2}{3}(x^2 - x + 1)} \]b) Studiare la funzione \( y = f(x) = \sqrt{\frac{2}{3}(x^2 - x + 1)} \) tralasciando i limiti geometrici, ma mettendo in evidenza nel grafico la parte che soddisfa tali limiti. Trovare, tra l'altro, le equazioni degli asintoti della curva.
c) Considerare il punto P del grafico della funzione di ascissa \( x_0 = 1 \). La tangente al grafico in P interseca i due asintoti obliqui nei punti R e S. Determinare l'area del triangolo avente per vertici i punti R, S e il punto V di intersezione dei due asintoti.
Soluzione Problema 4:
a) Verifica della formula della distanza (Geometria Euclidea)
Figura rappresentativa del problema:
Costruzione geometrica:
Consideriamo il cubo ABCDEFGH con spigolo unitario. Sia M il punto medio dello spigolo AB. Dimostreremo che la distanza di P dalla diagonale AG può essere calcolata usando proprietà geometriche del cubo.
Proprietà della diagonale AG:
- La diagonale AG ha lunghezza \(\sqrt{3}\) (diagonale spaziale del cubo)
- AG forma angoli uguali con tutti e tre gli spigoli uscenti da A
- La proiezione di AG sul piano ABCD è la diagonale AC di lunghezza \(\sqrt{2}\)
Calcolo della distanza usando il triangolo APG:
Il punto P ha coordinate sul sistema del cubo:
- P si trova sullo spigolo BF a distanza x da B
- Possiamo calcolare AP usando il teorema di Pitagora nel piano e nello spazio
Dato che P è sullo spigolo BF con BP = x:
\[ AP^2 = AB^2 + BP^2 = 1^2 + x^2 = 1 + x^2 \]Analogamente, per PG (dove G è vertice opposto ad A):
\[ PG^2 = PF^2 + FG^2 = (1-x)^2 + (\sqrt{2})^2 = 1 - 2x + x^2 + 2 = x^2 - 2x + 3 \]Formula della distanza di P dalla retta AG (che indichiamo con y=PK)
La distanza y di P dalla retta AG si può calcolare usando l'area del triangolo APG:
\[ \text{Area}(APG) = \frac{1}{2} \cdot AG \cdot y \]Dati noti del Triangolo APG:
- \(AP^2 = 1 + x^2 \Rightarrow AP = \sqrt{1 + x^2}\)
- \(AG^2 = 3 \Rightarrow AG = \sqrt{3}\) (Diagonale del cubo)
- \(PG^2 = 1^2 + 1^2 + (1-x)^2 = x^2 - 2x + 2 \Rightarrow PG = \sqrt{x^2 - 2x + 2}\)
Sia \( y = PK \) la distanza (altezza) del punto \( P \) dalla retta \( AG \), con \( K \) sulla retta \( AG \).
1. Calcolo della Proiezione \( AK \)
Utilizziamo il Teorema di Pitagora Generalizzato (o di Carnot), valido per il lato \( PG \) opposto all'angolo acuto in \( A \). Il teorema afferma che, in un triangolo acutangolo, il quadrato del lato opposto a un angolo acuto è uguale alla somma dei quadrati degli altri due lati diminuita del doppio prodotto fra uno dei due lati e la sua proiezione sull'altro lato.
Applichiamo la relazione al lato \( PG \), dove \( AK \) è la proiezione di \( AP \) sul lato \( AG \):
\[ PG^2 = AP^2 + AG^2 - 2 \cdot AG \cdot AK \]Sostituendo i valori:
\[ (x^2 - 2x + 2) = (1 + x^2) + 3 - 2 \cdot \sqrt{3} \cdot AK \]Risolviamo per \( AK \):
\[ 2\sqrt{3} \cdot AK = (1 + x^2) + 3 - (x^2 - 2x + 2) \] \[ 2\sqrt{3} \cdot AK = x^2 + 4 - x^2 + 2x - 2 \] \[ 2\sqrt{3} \cdot AK = 2x + 2 \] \[ AK = \frac{x + 1}{\sqrt{3}} \]2. Calcolo della Distanza \( y = PK \)
Utilizziamo il Teorema di Pitagora sul triangolo rettangolo \( APK \):
\[ y^2 = PK^2 = AP^2 - AK^2 \]Sostituendo \( AP^2 \) e \( AK \):
\[ y^2 = (1 + x^2) - \left(\frac{x + 1}{\sqrt{3}}\right)^2 \] \[ y^2 = 1 + x^2 - \frac{x^2 + 2x + 1}{3} \]Portando a denominatore comune (3):
\[ y^2 = \frac{3(1 + x^2) - (x^2 + 2x + 1)}{3} \] \[ y^2 = \frac{3 + 3x^2 - x^2 - 2x - 1}{3} \] \[ y^2 = \frac{2x^2 - 2x + 2}{3} = \frac{2}{3}(x^2 - x + 1) \]Quindi, la distanza \( y \) è:
\[ y = \sqrt{\frac{2}{3}(x^2 - x + 1)} \]Come richiesto. ✓
b) Studio della funzione
Funzione da studiare:
\[ y = f(x) = \sqrt{\frac{2}{3}(x^2 - x + 1)} \]- Dominio: Il radicando deve essere non negativo. Studiamo \( x^2 - x + 1 \):
\[
x^2 - x + 1 = \left(x - \frac{1}{2}\right)^2 + \frac{3}{4} > 0 \quad \forall x \in \mathbb{R}
\]
Quindi il dominio naturale è \( \mathbb{R} \).
Il dominio geometrico è \( [0, 1] \). - Intersezioni con gli assi:
- Asse y (x = 0): \( y = \sqrt{\frac{2}{3} \cdot 1} = \sqrt{\frac{2}{3}} = \frac{\sqrt{6}}{3} \)
- Asse x (y = 0): Nessuna intersezione, poiché \( f(x) > 0 \) sempre.
- Parità/Disparità: La funzione non è né pari né dispari.
- Segno: \( f(x) > 0 \) per ogni \( x \in \mathbb{R} \).
- Limiti: \[ \lim_{x \to \pm\infty} f(x) = \lim_{x \to \pm\infty} \sqrt{\frac{2}{3}} \cdot |x| \cdot \sqrt{1 - \frac{1}{x} + \frac{1}{x^2}} = +\infty \]
- Asintoti obliqui:
La funzione \( y = f(x) \) ammette asintoti obliqui \( y = mx + q \), dove:
\[ m = \lim_{x \to \pm\infty} \frac{f(x)}{x} \quad \text{e} \quad q = \lim_{x \to \pm\infty} [f(x) - mx] \]Per \( x \to +\infty \): Asintoto destro (\( y = m_R x + q_R \))
Calcolo di \( m_R \):
\[ m_R = \lim_{x \to +\infty} \frac{\sqrt{\frac{2}{3}(x^2 - x + 1)}}{x} = \sqrt{\frac{2}{3}} \cdot \lim_{x \to +\infty} \frac{|x| \sqrt{1 - \frac{1}{x} + \frac{1}{x^2}}}{x} \]Poiché \( x > 0 \), \( |x| = x \):
\[ m_R = \sqrt{\frac{2}{3}} \cdot \lim_{x \to +\infty} \frac{x \sqrt{1 - \frac{1}{x} + \frac{1}{x^2}}}{x} = \sqrt{\frac{2}{3}} = \frac{\sqrt{6}}{3} \]Calcolo di \( q_R \):
\[ q_R = \lim_{x \to +\infty} \left[\sqrt{\frac{2}{3}(x^2 - x + 1)} - \frac{\sqrt{6}}{3} x\right] = \sqrt{\frac{2}{3}} \lim_{x \to +\infty} \left[\sqrt{x^2 - x + 1} - x\right] \]Moltiplichiamo e dividiamo per il coniugato:
\[ q_R = \sqrt{\frac{2}{3}} \lim_{x \to +\infty} \frac{(x^2 - x + 1) - x^2}{\sqrt{x^2 - x + 1} + x} = \sqrt{\frac{2}{3}} \lim_{x \to +\infty} \frac{-x + 1}{x \sqrt{1 - \frac{1}{x} + \frac{1}{x^2}} + x} \]Dividendo numeratore e denominatore per \( x \):
\[ q_R = \sqrt{\frac{2}{3}} \cdot \frac{-1}{1 + 1} = -\frac{1}{2}\sqrt{\frac{2}{3}} = -\frac{\sqrt{6}}{6} \]Asintoto obliquo destro (\( a_R \)):
\[ y = \frac{\sqrt{6}}{3} x - \frac{\sqrt{6}}{6} = \frac{\sqrt{6}}{3}\left(x - \frac{1}{2}\right) \]Per \( x \to -\infty \): Asintoto sinistro (\( y = m_S x + q_S \))
Calcolo di \( m_S \):
\[ m_S = \lim_{x \to -\infty} \frac{f(x)}{x} = \sqrt{\frac{2}{3}} \cdot \lim_{x \to -\infty} \frac{|x| \sqrt{...}}{x} \]Poiché \( x < 0 \), \( |x| = -x \):
\[ m_S = \sqrt{\frac{2}{3}} \cdot \lim_{x \to -\infty} \frac{-x \sqrt{...}}{x} = -\sqrt{\frac{2}{3}} = -\frac{\sqrt{6}}{3} \]Calcolo di \( q_S \):
\[ q_S = \lim_{x \to -\infty} \left[\sqrt{\frac{2}{3}(x^2 - x + 1)} + \frac{\sqrt{6}}{3} x\right] = \sqrt{\frac{2}{3}} \lim_{x \to -\infty} \left[\sqrt{x^2 - x + 1} + x\right] \]Moltiplicando e dividendo per il coniugato:
\[ q_S = \sqrt{\frac{2}{3}} \lim_{x \to -\infty} \frac{-x + 1}{\sqrt{x^2 - x + 1} - x} \]Dividendo numeratore e denominatore per \( x \):
\[ q_S = \sqrt{\frac{2}{3}} \cdot \frac{-1}{-\sqrt{1} - 1} = \frac{1}{2}\sqrt{\frac{2}{3}} = \frac{\sqrt{6}}{6} \]Asintoto obliquo sinistro (\( a_S \)):
\[ y = -\frac{\sqrt{6}}{3} x + \frac{\sqrt{6}}{6} = -\frac{\sqrt{6}}{3}\left(x - \frac{1}{2}\right) \]Punto di intersezione degli asintoti:
I due asintoti si intersecano quando:
\[ \frac{\sqrt{6}}{3}\left(x - \frac{1}{2}\right) = -\frac{\sqrt{6}}{3}\left(x - \frac{1}{2}\right) \]Questo è vero solo per \( x = \frac{1}{2} \), che dà \( y = 0 \).
Punto di intersezione: \( V = \left(\frac{1}{2}, 0\right) \)
- Monotonia:
Derivata prima:
\[ f'(x) = \sqrt{\frac{2}{3}} \cdot \frac{2x - 1}{2\sqrt{x^2 - x + 1}} \]Semplificando usando \( f(x) = \sqrt{\frac{2}{3}(x^2 - x + 1)} \):
\[ f'(x) = \frac{2x - 1}{3f(x)} \]Studio del segno:
\[ f'(x) > 0 \Leftrightarrow 2x - 1 > 0 \Leftrightarrow x > \frac{1}{2} \]- Decrescente in \( \left(-\infty, \frac{1}{2}\right) \)
- Crescente in \( \left(\frac{1}{2}, +\infty\right) \)
- Minimo assoluto in \( x = \frac{1}{2} \): \[ f\left(\frac{1}{2}\right) = \sqrt{\frac{2}{3} \cdot \frac{3}{4}} = \sqrt{\frac{1}{2}} = \frac{\sqrt{2}}{2} \]
Grafico:
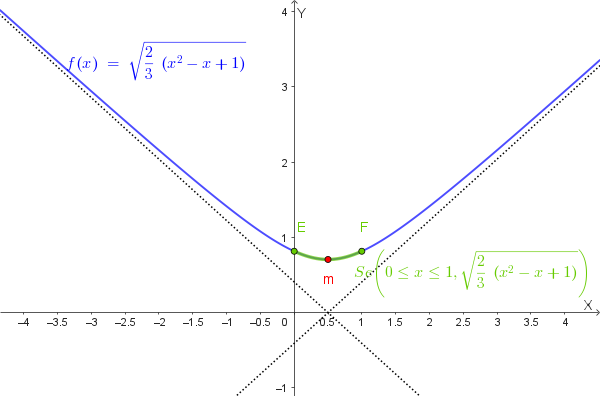
Il grafico della funzione mostra:
- Due asintoti obliqui simmetrici che si intersecano in \( \left(\frac{1}{2}, 0\right) \)
- Minimo in \( \left(\frac{1}{2}, \frac{\sqrt{2}}{2}\right) \)
- La parte che soddisfa i limiti geometrici \( x \in [0, 1] \) è evidenziata in verde
c) Area del triangolo
Punto P con \( x_0 = 1 \):
\[ y_0 = \sqrt{\frac{2}{3}(1 - 1 + 1)} = \sqrt{\frac{2}{3}} = \frac{\sqrt{6}}{3} \]Quindi: \( P = \left(1, \frac{\sqrt{6}}{3}\right) \)
Coefficiente angolare della tangente:
\[ m = f'(1) = \frac{2(1) - 1}{3 \cdot \frac{\sqrt{6}}{3}} = \frac{1}{\sqrt{6}} = \frac{\sqrt{6}}{6} \]Equazione della tangente:
\[ y - \frac{\sqrt{6}}{3} = \frac{\sqrt{6}}{6}(x - 1) \] \[ y = \frac{\sqrt{6}}{6}x - \frac{\sqrt{6}}{6} + \frac{\sqrt{6}}{3} = \frac{\sqrt{6}}{6}x + \frac{\sqrt{6}}{6} \] \[ y = \frac{\sqrt{6}}{6}(x + 1) \]Intersezione con asintoto destro (punto R):
Asintoto destro: \( y = \frac{\sqrt{6}}{3}\left(x - \frac{1}{2}\right) \)
\[ \frac{\sqrt{6}}{6}(x + 1) = \frac{\sqrt{6}}{3}\left(x - \frac{1}{2}\right) \] \[ x + 1 = 2\left(x - \frac{1}{2}\right) = 2x - 1 \] \[ x = 2 \] \[ y = \frac{\sqrt{6}}{6}(2 + 1) = \frac{3\sqrt{6}}{6} = \frac{\sqrt{6}}{2} \]Punto R: \( \left(2, \frac{\sqrt{6}}{2}\right) \)
Intersezione con asintoto sinistro (punto S):
Asintoto sinistro: \( y = -\frac{\sqrt{6}}{3}\left(x - \frac{1}{2}\right) \)
\[ \frac{\sqrt{6}}{6}(x + 1) = -\frac{\sqrt{6}}{3}\left(x - \frac{1}{2}\right) \] \[ x + 1 = -2\left(x - \frac{1}{2}\right) = -2x + 1 \] \[ 3x = 0 \Rightarrow x = 0 \] \[ y = \frac{\sqrt{6}}{6}(0 + 1) = \frac{\sqrt{6}}{6} \]Punto S: \( \left(0, \frac{\sqrt{6}}{6}\right) \)
Area del triangolo VRS:
I tre vertici sono:
- \( V = \left(\frac{1}{2}, 0\right) \)
- \( R = \left(2, \frac{\sqrt{6}}{2}\right) \)
- \( S = \left(0, \frac{\sqrt{6}}{6}\right) \)
Per calcolare l'area utilizziamo la formula geometrica base x altezza / 2, dove la base è il segmento \( SR \) e l'altezza \( h \) è la distanza del vertice \( V \) dalla retta \(SR\) (che è la tangente \( t \) in \( P \)).
1. Calcolo della Base (\( b = d(S, R) \))
\[ b = \sqrt{(x_R - x_S)^2 + (y_R - y_S)^2} \] \[ b = \sqrt{(2 - 0)^2 + \left(\frac{\sqrt{6}}{2} - \frac{\sqrt{6}}{6}\right)^2} = \sqrt{4 + \left(\frac{3\sqrt{6} - \sqrt{6}}{6}\right)^2} \] \[ b = \sqrt{4 + \left(\frac{2\sqrt{6}}{6}\right)^2} = \sqrt{4 + \frac{6}{9}} = \sqrt{\frac{12 + 2}{3}} = \frac{\sqrt{42}}{3} \]2. Calcolo dell'Altezza (\( h = d(V, t) \))
La retta \( SR \) (tangente \( r \)) ha equazione: \( \sqrt{6}x - 6y + \sqrt{6} = 0 \).
\[ h = \frac{|Ax_V + By_V + C|}{\sqrt{A^2 + B^2}} = \frac{\left|\sqrt{6}\left(\frac{1}{2}\right) - 6(0) + \sqrt{6}\right|}{\sqrt{(\sqrt{6})^2 + (-6)^2}} \] \[ h = \frac{\left|\frac{\sqrt{6}}{2} + \sqrt{6}\right|}{\sqrt{42}} = \frac{\frac{3\sqrt{6}}{2}}{\sqrt{42}} = \frac{3\sqrt{6}}{2\sqrt{42}} \]3. Calcolo dell'Area
\[ \text{Area} = \frac{1}{2} \cdot b \cdot h = \frac{1}{2} \cdot \frac{\sqrt{42}}{3} \cdot \frac{3\sqrt{6}}{2\sqrt{42}} \]Semplificando \( \sqrt{42} \) e \( 3 \):
\[ \text{Area} = \frac{1}{2} \cdot \frac{\sqrt{6}}{2} = \frac{\sqrt{6}}{4} \]Risposta:
\[ \boxed{\text{Area} = \frac{\sqrt{6}}{4}} \]