Risolvi da solo i quesiti e controlla le soluzioni premendo (una o due volte) il tasto corrispondente.
a)
studiare le funzioni:
\( y=f(x)=\frac{-2x^3+6x^2}{3} \), \( y=g(x)=\frac{x^3-6x^2+12x}{3} \)
e disegnare i loro grafici.
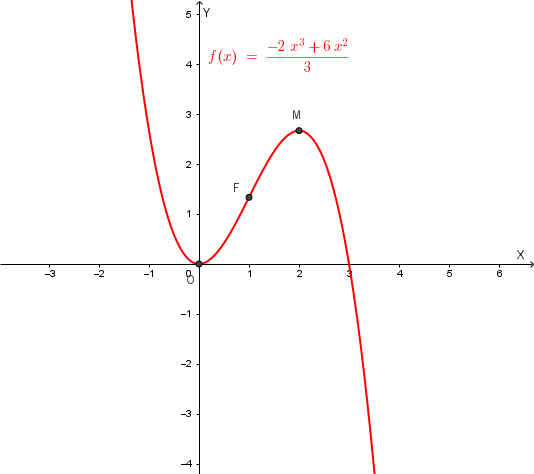
Studiamo la funzione:
\( y=f(x)=\frac{-2x^3+6x^2}{3}=-\frac{2}{3}x^3+2x^2=x^2(-\frac{2}{3}x+2) \)
Si tratta di una cubica, quindi è definita su tutto R.
La funzione non è né pari né dispari.
Intersezioni con gli assi cartesiani:
Se \( x=0 \), \( y=0 \).
Se \( y=0 \), \( x=0 \) (doppia, quindi tangenza all'asse x) e \( -\frac{2}{3}x+2=0 \) da cui \( x=3 \).
Limiti:
\( \lim_{x \to \pm\infty} (-\frac{2}{3}x^3+2x^2) = \lim_{x \to \pm\infty} (-\frac{2}{3}x^3) = \mp\infty \) (non ci sono asintoti obliqui).
Derivata prima:
\( f'(x) = -2x^2+4x \geq 0 \) se \( x^2-2x \leq 0 \): \( 0 \leq x \leq 2 \).
La funzione è quindi crescente se \( 0 < x < 2 \) e decrescente se \( x < 0 \) o \( x > 2 \).
\( x=2 \) è punto di massimo relativo con valore \( f(2)=-\frac{2}{3} \cdot 8 + 8 = \frac{8}{3} \);
\( x=0 \) è punto di minimo relativo con valore \( y=0 \).
Derivata seconda:
\( f''(x) = -4x+4 \geq 0 \) se \( x \leq 1 \): concavità verso l'alto se \( x < 1 \), verso il basso se \( x > 1 \), flesso per \( x=1 \) con \( y=f(1)=-\frac{2}{3}+2=\frac{4}{3} \).
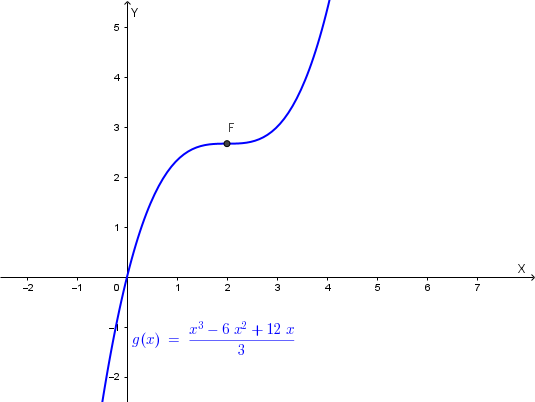
Studiamo la seconda funzione:
\( y=g(x)=\frac{x^3-6x^2+12x}{3}=\frac{1}{3}x^3-2x^2+4x=x(\frac{1}{3}x^2-2x+4) \)
Si tratta di una cubica, quindi è definita su tutto R.
La funzione non è né pari né dispari.
Intersezioni con gli assi cartesiani:
Se \( x=0 \), \( y=0 \).
Se \( y=0 \), \( x=0 \) e \( \frac{1}{3}x^2-2x+4=0 \) che non ha soluzioni (delta negativo).
Limiti:
\( \lim_{x \to \pm\infty} (\frac{1}{3}x^3-2x^2+4x) = \lim_{x \to \pm\infty} (\frac{1}{3}x^3) = \pm\infty \) (non ci sono asintoti obliqui).
Derivata prima:
\( g'(x) = x^2-4x+4 \geq 0 \) se \( (x-2)^2 \geq 0 \): per ogni \( x \); in particolare \( g'(x)=0 \) se \( x=2 \).
Quindi la funzione è sempre crescente ed ha in \( x=2 \) (ordinata \( y=g(2)=\frac{8}{3}-8+8=\frac{8}{3} \)) un flesso a tangente orizzontale.
Derivata seconda:
\( g''(x) = 2x-4 \geq 0 \) se \( x \geq 2 \): concavità verso l'alto se \( x > 2 \), verso il basso se \( x < 2 \), flesso per \( x=2 \) con \( y=g(2)=\frac{8}{3} \).
b)
Dopo aver verificato che, oltre al punto O, tali grafici hanno in comune un altro punto A, determinare sul segmento OA un punto P tale che, condotta per esso la retta parallela all'asse y, sia massima la lunghezza del segmento RS, dove R ed S sono i punti in cui la retta interseca i due grafici suddetti.
Cerchiamo le intersezioni fra le due curve:
\[ \begin{cases} y = \frac{1}{3}x^3-2x^2+4x \\ y = -\frac{2}{3}x^3+2x^2 \end{cases} \]Uguagliando le due espressioni:
\[ \frac{1}{3}x^3-2x^2+4x = -\frac{2}{3}x^3+2x^2 \implies x^3-4x^2+4x = 0 \implies x(x^2-4x+4) = 0 \]Quindi: \( x=0 \) e \( x=2 \) (doppia).
Se \( x=0 \): \( y=0 \), se \( x=2 \): \( y=\frac{8}{3} \).
Quindi i due grafici, oltre al punto O hanno in comune il punto \( A=(2;\frac{8}{3}) \).
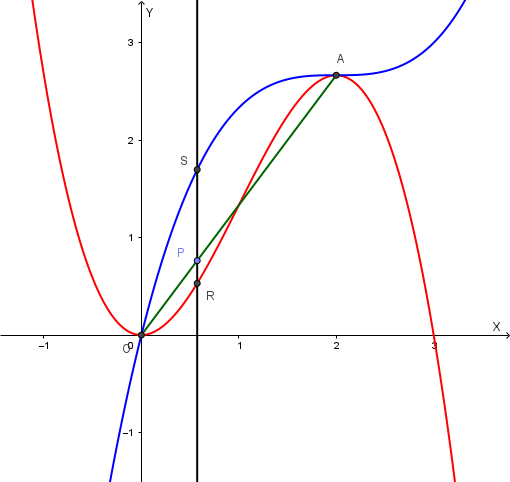
\( O=(0;0) \), \( A=(2;\frac{8}{3}) \), retta OA: \( y=\frac{4}{3}x \), \( P=(t;\frac{4}{3}t) \), retta r: \( x=t \), con \( 0 \leq t \leq 2 \).
Punto R:
\[ \begin{cases} x = t \\ y = -\frac{2}{3}x^3+2x^2 \end{cases} \implies R=(t;-\frac{2}{3}t^3+2t^2) \]Punto S:
\[ \begin{cases} x = t \\ y = \frac{1}{3}x^3-2x^2+4x \end{cases} \implies S=(t;\frac{1}{3}t^3-2t^2+4t) \]La lunghezza RS è quindi:
\[ z = y_S - y_R = \frac{1}{3}t^3-2t^2+4t - (-\frac{2}{3}t^3+2t^2) = t^3-4t^2+4t, \quad 0 \leq t \leq 2 \]Dobbiamo determinare il massimo di z.
\( z' = 3t^2-8t+4 \geq 0 \) se \( t \leq \frac{2}{3} \) o \( t \geq 2 \), quindi z è crescente se \( 0 \leq t < \frac{2}{3} \) e decrescente se \( \frac{2}{3} < t < 2 \): z è massima se \( t = \frac{2}{3} \).
Il punto P richiesto è quindi il punto della retta di equazione \( y=\frac{4}{3}x \) con ascissa \( \frac{2}{3} \):
\( P=(\frac{2}{3};\frac{8}{9}) \).
Per \( t = \frac{2}{3} \), le coordinate dei punti \( R \) ed \( S \) sono:
\[ R = \left( \frac{2}{3}, \frac{56}{81} \right), \quad S = \left( \frac{2}{3}, \frac{152}{81} \right) \]c)
Determinare le coordinate dei punti di ascisse uguali in cui le due curve hanno tangenti parallele e verificare che, oltre al punto A, si ritrovano i punti R ed S.
Dobbiamo imporre che sia \( f'(x) = g'(x) \), quindi:
\[ -2x^2+4x = x^2-4x+4 \implies 3x^2-8x+4 = 0 \]Soluzioni: \( x = \frac{2}{3} \) e \( x = 2 \).
Per \( x = \frac{2}{3} \) troviamo R ed S e per \( x = 2 \) troviamo A.
d)
Calcolare l'area della regione finita di piano delimitata dalle due curve.
Rappresentiamo la regione di cui si chiede l'area:
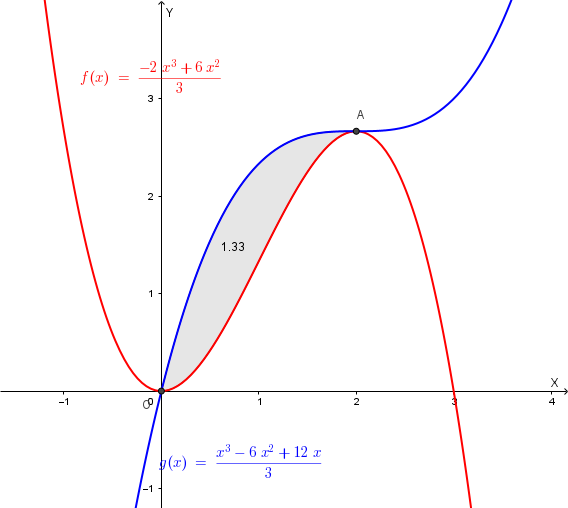
L'area richiesta si ottiene calcolando il seguente integrale:
\[ \text{Area} = \int_0^2 [g(x)-f(x)] dx = \int_0^2 \left[\frac{1}{3}x^3-2x^2+4x - (-\frac{2}{3}x^3+2x^2)\right] dx \] \[ = \int_0^2 [x^3-4x^2+4x] dx = \left[\frac{x^4}{4}-\frac{4}{3}x^3+2x^2\right]_0^2 = 4 - \frac{32}{3} + 8 = \frac{4}{3} \text{ u}^2 \]