

Risolvi da solo i vari punti del problema e controlla le soluzioni premendo il tasto corrispondente.
a)
Dimostrare che:
- \( f_a \) è una funzione pari \( \forall a \in \mathbb{R} \);
- \( f_a \) ha dominio \( D = \mathbb{R} \) se e solo se \( a > 0 \);
- \( f_a \) è derivabile \( \forall x \in \mathbb{R} \) se e solo se \( a = 1 \).
Dimostriamo che \( f_a \) è pari per ogni valore di \( a \).
\[ f_a(x) = \frac{e^{|x|+a}}{|x|+a} \]
\[ f_a(-x) = \frac{e^{|-x|+a}}{|-x|+a} = \frac{e^{|x|+a}}{|x|+a} = f_a(x) \]
Quindi la funzione è pari per ogni valore di \( a \).
Dimostriamo che \( f_a \) ha dominio \( D = \mathbb{R} \) se e solo se \( a > 0 \).
Il dominio della funzione è dato da: \( |x| + a \neq 0 \); ciò avviene per ogni \( x \) se e solo se \( a > 0 \).
Dimostriamo che \( f_a \) è derivabile \( \forall x \in \mathbb{R} \) se e solo se \( a = 1 \).
\[ f_a(x) = \begin{cases} \frac{e^{-x + a}}{-x + a} & \text{se } x < 0 \\ \frac{e^a}{a} & \text{se } x = 0 \\ \frac{e^{x + a}}{x + a} & \text{se } x > 0 \end{cases} \]
Siccome se \( a = 0 \) non esiste \( f_a(0) \), la funzione non può essere derivabile \( \forall x \in \mathbb{R} \) se \( a = 0 \).
Per essere derivabile su tutto \( \mathbb{R} \) dobbiamo quindi porre \( a \neq 0 \).
Osserviamo che se \( x < 0 \) la funzione non è definita quando \( -x + a = 0 \), cioè \( x = a \). Quindi non può essere \( a < 0 \), perché altrimenti la funzione non è continua in \( x = a \).
Osserviamo che per \( a > 0 \) la funzione è derivabile per \( x < 0 \) e per \( x > 0 \) essendo:
Se \( x < 0 \): \[ f'_a(x) = \frac{(-e^{-x + a})(-x + a) + e^{-x + a}}{(-x + a)^2} \] che esiste per ogni \( x \neq a \) (sempre verificato perché \( a > 0 \))
Se \( x > 0 \): \[ f'_a(x) = \frac{(e^{x + a})(x + a) - e^{x + a}}{(x + a)^2} \] che esiste per ogni \( x \neq -a \) (sempre verificato perché \( a > 0 \))
La funzione è derivabile su tutto \( \mathbb{R} \) se e solo se lo è in \( x = 0 \). Osserviamo che per \( x = 0 \) la funzione è continua, essendo:
\[ \lim_{x \to 0^-} \frac{e^{-x + a}}{-x + a} = \frac{e^a}{a} = \lim_{x \to 0^+} \frac{e^{x + a}}{x + a} = f_a(0) \]Per la condizione sufficiente di derivabilità la funzione sarà derivabile in \( x = 0 \) se:
\[ \lim_{x \to 0^-} f'_a(x) = \lim_{x \to 0^+} f'_a(x) = l \text{ (finito)} \]\[ \lim_{x \to 0^-} f'_a(x) = \lim_{x \to 0^-} \frac{(-e^{-x + a})(-x + a) + e^{-x + a}}{(-x + a)^2} = \frac{-e^a(a) + e^a}{a^2} = -\frac{e^a}{a^2}(a - 1) \]
\[ \lim_{x \to 0^+} f'_a(x) = \lim_{x \to 0^+} \frac{(e^{x + a})(x + a) - e^{x + a}}{(x + a)^2} = \frac{e^a(a) - e^a}{a^2} = \frac{e^a}{a^2}(a - 1) \]
Deve quindi essere:
\[ -\frac{e^a}{a^2}(a - 1) = \frac{e^a}{a^2}(a - 1) \]da cui:
\[ a - 1 = 1 - a \implies a = 1 \]Abbiamo quindi dimostrato che \( f_a \) è derivabile \( \forall x \in \mathbb{R} \) se e solo se \( a = 1 \).
b)
Poniamo d'ora in poi \( a = 1 \).
Studiare la funzione \( f_1 \) e tracciare il suo grafico rappresentativo \( \Gamma \).
\[ f_1(x) = \frac{e^{|x| + 1}}{|x| + 1} \]
Ricordiamo che il grafico della funzione \( f(|x|) \) si ottiene da quello di \( f(x) \) confermando la parte del grafico di \( f(x) \) che si ha per \( x > 0 \) e ribaltando tale parte rispetto all'asse delle ordinate.
Nel nostro caso, posto \( f(x) = \frac{e^{x + 1}}{x + 1} \) risulta \( f_1(x) = f(|x|) \), per ottenere \( \Gamma \) è sufficiente studiare la funzione:
\[ y = f(x) = \frac{e^{x + 1}}{x + 1} \]
Questa si ottiene dalla più semplice \( y = g(x) = \frac{e^x}{x} \) con una traslazione verso sinistra di vettore \( (-1, 0) \).
Procediamo quindi con lo studio della funzione \( y = \frac{e^x}{x} \).
Dominio: \( (-\infty, 0) \cup (0, +\infty) \)
Non ci sono intersezioni con gli assi cartesiani.
Calcolando \( f(-x) \) si vede che la funzione non è pari né dispari.
È positiva per \( x > 0 \) e negativa per \( x < 0 \).
Calcolo dei limiti alla frontiera del dominio:
\[ \lim_{x \to -\infty} \frac{e^x}{x} = \left[ \frac{0^+}{-\infty} \right] = 0^- \]
\[ \lim_{x \to +\infty} \frac{e^x}{x} = \left[ \frac{+\infty}{+\infty} \right] = +\infty \] ( \( e^x \) è infinito di ordine superiore rispetto ad \( x \) )
\[ \lim_{x \to 0^-} \frac{e^x}{x} = \left[ \frac{1}{0^-} \right] = -\infty \]
\[ \lim_{x \to 0^+} \frac{e^x}{x} = \left[ \frac{1}{0^+} \right] = +\infty \]
Asintoto verticale \( x = 0 \). Asintoto orizzontale \( y = 0 \) per \( x \to -\infty \).
Possibile asintoto obliquo per \( x \to +\infty \):
\[ \lim_{x \to +\infty} \frac{\frac{e^x}{x}}{x} = \lim_{x \to +\infty} \frac{e^x}{x^2} = +\infty \] ( \( e^x \) è infinito di ordine superiore rispetto ad \( x^2 \) ): no asintoto obliquo
Studio della derivata prima:
\[ g'(x) = \frac{e^x(x) - e^x(1)}{x^2} = \frac{e^x(x - 1)}{x^2} \]
\( g'(x) = 0 \) per \( x = 1 \): punto stazionario.
\( g'(x) > 0 \) per \( x > 1 \), \( g'(x) < 0 \) per \( x < 0 \) e \( 0 < x < 1 \).
La funzione è quindi decrescente per \( x < 0 \) e \( 0 < x < 1 \) e crescente per \( x > 1 \).
\( x = 1 \) è punto di minimo relativo (con ordinata \( y = e \)): \( m = (1, e) \).
Studio della derivata seconda:
\[ g''(x) = \frac{[e^x(x - 1) + e^x(1)]x^2 - e^x(x - 1)(2x)}{x^4} = \cdots = \frac{e^x(x^2 - 2x + 2)}{x^3} \]
Essendo \( x^2 - 2x + 2 > 0 \) per ogni \( x \) (il discriminante è minore di zero), la derivata seconda è positiva per \( x > 0 \) (concavità del grafico verso l'alto) e negativa per \( x < 0 \) (concavità verso il basso).
Non ci sono flessi.
Il grafico di \( y = g(x) = \frac{e^x}{x} \) è quindi il seguente:
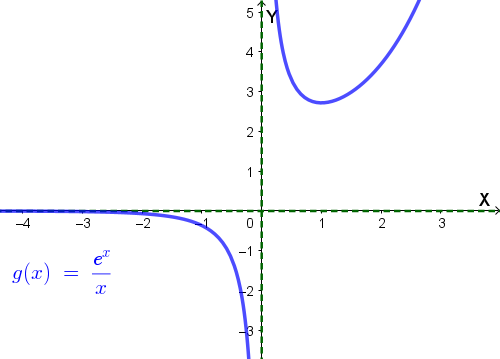
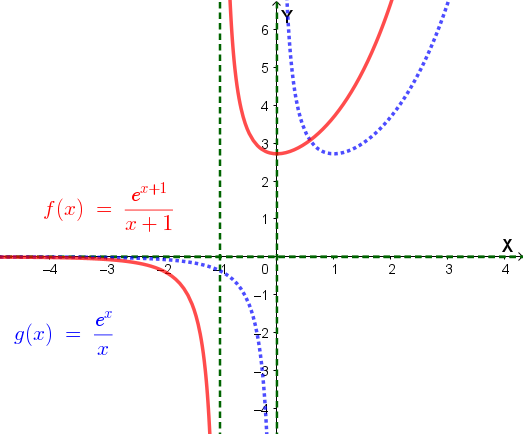
Il grafico di \( y = f(x) = \frac{e^{x + 1}}{x + 1} \), si ottiene dal precedente traslandolo a sinistra di 1 (taglia l'asse delle ordinate in \( y = e \), che è minimo relativo per \( x = 0 \)).
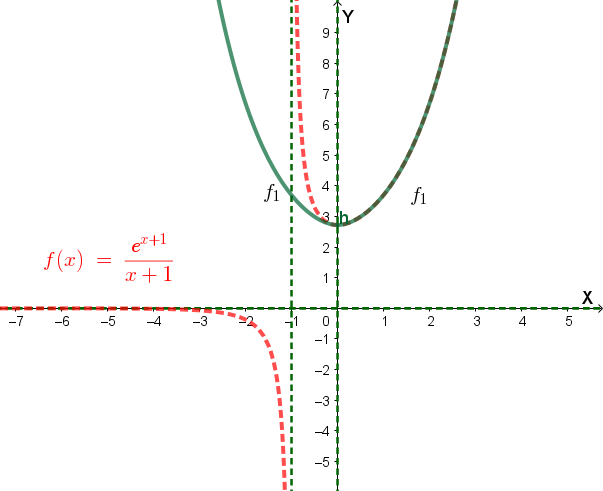
Infine, il grafico \( \Gamma \) (in verde) della funzione richiesta \( f_1(x) = \frac{e^{|x| + 1}}{|x| + 1} \) si ottiene (come già detto) da quello di \( f \) confermando la sua parte a destra dell'asse delle ordinate e ribaltandola a sinistra dello stesso asse:
c)
Determinare l'equazione della retta tangente al grafico \( \Gamma \) nel suo punto di ascissa 1.
\[ f_1(x) = \frac{e^{|x| + 1}}{|x| + 1} \]
Il punto richiesto ha coordinate \( P = (1, \frac{e^2}{2}) \).
Ricordiamo che per \( x > 0 \) è \( f_1(x) = \frac{e^{x + 1}}{x + 1} \), quindi:
\[ f'_1(x) = \frac{e^{x + 1}(x + 1) - e^{x + 1}}{(x + 1)^2} = \frac{x e^{x + 1}}{(x + 1)^2} \]
Il coefficiente angolare della tangente in \( P \) è quindi:
\[ m = f'_1(1) = \frac{e^2}{4} \]
Tangente in \( P \):
\[ y - \frac{e^2}{2} = \frac{e^2}{4}(x - 1) \implies y = \frac{e^2}{4}x + \frac{1}{4}e^2 \]
d)
A partire dal grafico di \( \Gamma \), dedurre il grafico \( \Omega \) della curva di equazione \( g(x) = \frac{1}{f_1(x)} \). Determinare l'area della regione finita di piano delimitato da \( \Omega \), dall'asse delle ascisse e dalle rette \( x = -1 \) e \( x = 1 \).
Studiamo la funzione \( g(x) \), a partire dal grafico di \( f_1(x) \).
Dominio: tutto \( \mathbb{R} \) (\( f_1(x) \) è sempre positiva)
Essendo \( f_1(x) \) pari, anche \( g(x) \) sarà pari (grafico simmetrico rispetto all'asse delle ordinate).
Intersezioni con gli assi cartesiani:
Se \( x = 0 \), \( g(0) = \frac{1}{f_1(0)} = \frac{1}{e} \approx 0.4 \). Se \( y = 0 \), \( \frac{1}{f_1(x)} = 0 \) mai (non viene intersecato l'asse delle ascisse).
Segno:
Essendo \( f_1(x) > 0 \) sempre, anche \( g(x) > 0 \) sempre.
Limiti agli estremi del dominio \( -\infty < x < +\infty \):
\[ \lim_{x \to \mp \infty} g(x) = \lim_{x \to -\infty} \frac{1}{f_1(x)} = \left[ \frac{1}{+\infty} \right] = 0^+ \]
\( y = 0 \) asintoto orizzontale.
Monotonia:
Per \( x < 0 \), \( f_1(x) \) è positiva e decrescente, quindi \( g(x) = \frac{1}{f_1(x)} \) sarà positiva e crescente.
Per \( x > 0 \), \( f_1(x) \) è positiva e crescente, quindi \( g(x) = \frac{1}{f_1(x)} \) sarà positiva e decrescente.
\( x = 0 \) è punto di minimo relativo per \( f_1(x) \), quindi sarà punto di massimo relativo per \( g(x) \) e la sua ordinata è \( \frac{1}{e} \).
Il grafico di \( g(x) \) sarà quindi del tipo (blu a tratto pieno) indicato nella seguente figura:
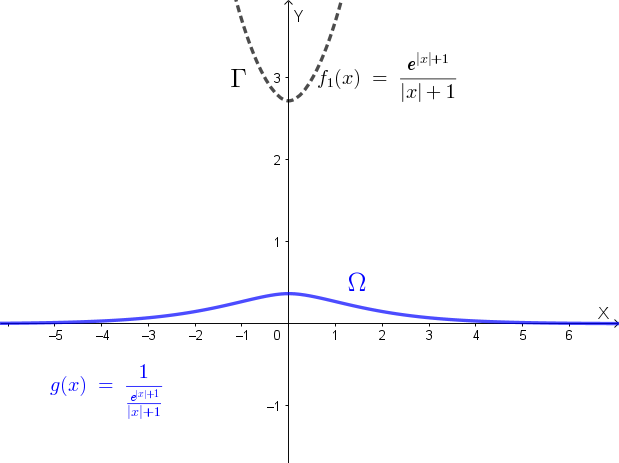
Calcoliamo la derivata seconda \( g''(x) \) per \( x > 0 \):
Partiamo dalla funzione \( g(x) = \frac{1}{f_1(x)} = \frac{x + 1}{e^{x + 1}} \) per \( x > 0 \).
Prima derivata \( g'(x) \):
\[ g'(x) = \frac{d}{dx}\left( \frac{x + 1}{e^{x + 1}} \right) \]
Applicando la regola del quoziente:
\[ g'(x) = \frac{(1) \cdot e^{x + 1} - (x + 1) \cdot e^{x + 1}}{(e^{x + 1})^2} \]
\[ g'(x) = \frac{e^{x + 1} [1 - (x + 1)]}{e^{2x + 2}} \]
\[ g'(x) = \frac{-x}{e^{x + 1}} \]
Seconda derivata \( g''(x) \):
\[ g''(x) = \frac{d}{dx}\left( \frac{-x}{e^{x + 1}} \right) \]
Nuovamente applicando la regola del quoziente:
\[ g''(x) = \frac{(-1) \cdot e^{x + 1} - (-x) \cdot e^{x + 1}}{(e^{x + 1})^2} \]
\[ g''(x) = \frac{e^{x + 1} [-1 + x]}{e^{2x + 2}} \]
\[ g''(x) = \frac{x - 1}{e^{x + 1}} \]
Quindi abbiamo dimostrato che:
\[ g''(x) = \frac{x - 1}{e^{x + 1}} \]
Questa derivata seconda si annulla quando \( x = 1 \), indicando un punto di flesso in \( x = 1 \). Per simmetria, avremo un altro flesso in \( x = -1 \).
Dobbiamo ora determinare l'area della regione finita di piano delimitato da \( \Omega \), dall'asse delle ascisse e dalle rette \( x = -1 \) e \( x = 1 \).
Per la simmetria di \( \Omega \) rispetto all'asse delle ordinate l'area richiesta è il doppio dell'area della regione rappresentata nella figura seguente:
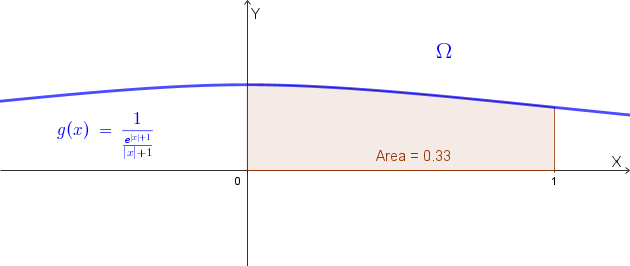
L'area richiesta è quindi data da:
\[ \text{Area} = 2 \int_0^1 g(x) dx = 2 \int_0^1 \frac{x + 1}{e^{x + 1}} dx \]
Cerchiamo una primitiva di \( \frac{x + 1}{e^{x + 1}} = (x + 1) e^{-x - 1} \) integrando per parti:
\[ \int (x + 1) e^{-x - 1} dx = \int (x + 1)(-e^{-x - 1})' dx = \left[ (-e^{-x - 1})(x + 1) - \int (1)(-e^{-x - 1}) dx \right] \]
\[ = -(x + 1) e^{-x - 1} - e^{-x - 1} = -e^{-x - 1}(x + 2) + c \]
Quindi:
\[ \text{Area} = 2 \int_0^1 \frac{x + 1}{e^{x + 1}} dx = 2 \left[ -e^{-x - 1}(x + 2) \right]_0^1 = 2(-3e^{-2} + 2e^{-1}) = \frac{4}{e} - \frac{6}{e^2} \approx 0.66 \text{ u}^2 \]