Risolvi da solo i vari punti del problema e controlla le soluzioni premendo il tasto corrispondente.
1)
Si determini il limite di \( f(x) \) per \( x \to +\infty \) e per \( x \to -\infty \). Si calcoli \( f(x)+f(-x) \) e si spieghi perché dal risultato si può dedurre che il punto \( A=(0; 1+\ln(4)) \) è centro di simmetria per \( \Gamma \).
Determinazione dei limiti
Calcoliamo il limite di \( f(x) \) per \( x \to +\infty \):
\[ \lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} \left( x+\ln(4)+\frac{2}{e^x+1} \right) \] \[ = \lim_{x \to +\infty} x + \lim_{x \to +\infty} \ln(4) + \lim_{x \to +\infty} \frac{2}{e^x+1} \] Poiché \( \lim_{x \to +\infty} x = +\infty \) e \( \lim_{x \to +\infty} \frac{2}{e^x+1} = \frac{2}{+\infty+1} = \frac{2}{+\infty} = 0 \), abbiamo: \[ \lim_{x \to +\infty} f(x) = +\infty + \ln(4) + 0 = +\infty \]Calcoliamo il limite di \( f(x) \) per \( x \to -\infty \):
\[ \lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} \left( x+\ln(4)+\frac{2}{e^x+1} \right) \] \[ = \lim_{x \to -\infty} x + \lim_{x \to -\infty} \ln(4) + \lim_{x \to -\infty} \frac{2}{e^x+1} \] Poiché \( \lim_{x \to -\infty} x = -\infty \) e \( \lim_{x \to -\infty} \frac{2}{e^x+1} = \frac{2}{0+1} = \frac{2}{1} = 2 \), abbiamo: \[ \lim_{x \to -\infty} f(x) = -\infty + \ln(4) + 2 = -\infty \]Calcolo di \( f(x)+f(-x) \) e deduzione del centro di simmetria
Calcoliamo \( f(-x) \):
\[ f(-x) = (-x)+\ln(4)+\frac{2}{e^{-x}+1} \] \[ = -x+\ln(4)+\frac{2}{\frac{1}{e^x}+1} \] \[ = -x+\ln(4)+\frac{2}{\frac{1+e^x}{e^x}} \] \[ = -x+\ln(4)+\frac{2e^x}{1+e^x} \]Ora calcoliamo \( f(x)+f(-x) \):
\[ f(x)+f(-x) = \left( x+\ln(4)+\frac{2}{e^x+1} \right) + \left( -x+\ln(4)+\frac{2e^x}{e^x+1} \right) \] \[ = x+\ln(4)+\frac{2}{e^x+1} -x+\ln(4)+\frac{2e^x}{e^x+1} \] \[ = 2\ln(4) + \frac{2+2e^x}{e^x+1} \] \[ = 2\ln(4) + \frac{2(1+e^x)}{e^x+1} \] \[ = 2\ln(4) + 2 \]Ricordando la proprietà dei logaritmi \( n \ln(a) = \ln(a^n) \), possiamo scrivere \( 2\ln(4) = \ln(4^2) = \ln(16) \).
Quindi:
\[ f(x)+f(-x) = 2\ln(4) + 2 \]Per dimostrare che un punto \( (x_0, y_0) \) è centro di simmetria per il grafico di una funzione \( f(x) \), deve valere la relazione generale:
\[ \frac{f(x_0+h) + f(x_0-h)}{2} = y_0 \]o, in forma equivalente, \( f(x_0+h) + f(x_0-h) = 2y_0 \). Questa condizione afferma che la media delle ordinate di due punti sulla curva, equidistanti da \(x_0\), deve coincidere con l'ordinata \(y_0\) del centro di simmetria.
Nel nostro caso, il punto proposto come centro di simmetria è \( A=(0; 1+\ln(4)) \). Ciò significa che \( x_0=0 \) e \( y_0=1+\ln(4) \).
Sostituendo \( x_0=0 \) e \( y_0=1+\ln(4) \) nella condizione di simmetria \( f(x_0+h) + f(x_0-h) = 2y_0 \), otteniamo:
\[ f(0+h) + f(0-h) = 2(1+\ln(4)) \]Che si semplifica in:
\[ f(h) + f(-h) = 2(1+\ln(4)) \]Poiché \( h \) è una variabile generica che può assumere qualsiasi valore, possiamo sostituirla con \( x \) per confrontarla direttamente con il nostro calcolo:
\[ f(x) + f(-x) = 2(1+\ln(4)) \]Abbiamo calcolato che \( f(x)+f(-x) = 2\ln(4) + 2 \).
Possiamo riscrivere \( 2\ln(4) + 2 \) come \( 2(\ln(4)+1) \).
Confrontando il nostro risultato \( 2(\ln(4)+1) \) con il valore \( 2y_0 = 2(1+\ln(4)) \), notiamo che sono esattamente uguali.
Dato che \( f(x)+f(-x) = 2(\ln(4)+1) \) è verificata, e il punto di simmetria ha ordinata \( y_0 = 1+\ln(4) \), la relazione di simmetria \( f(x_0+h) + f(x_0-h) = 2y_0 \) è soddisfatta per \( x_0=0 \) e \( y_0=1+\ln(4) \).
Quindi, il punto \( A=(0; 1+\ln(4)) \) è effettivamente centro di simmetria per \( \Gamma \).
2)
Si provi che, per tutti i reali \( m \), l'equazione \( f(x)=m \) ammette una ed una sola soluzione in \( \mathbb{R} \). Sia \( \alpha \) la soluzione dell'equazione \( f(x)=3 \); per quale valore di \( m \) il numero \( -\alpha \) è soluzione dell'equazione \( f(x)=-m \)?
\( f(x)=m \) equivale a \( f(x)-m=0 \). Pongo \( g(x)=f(x)-m \); questa funzione, in base a quanto detto sui limiti della \( f \), ha limite \( -\infty \) per \( x \to -\infty \) e \( +\infty \) per \( x \to +\infty \), pertanto ammette almeno uno zero.
Risulta poi:
\[ f'(x) = \frac{d}{dx}\left( x+\ln(4)+\frac{2}{e^x+1} \right) = 1 + 0 + 2 \frac{d}{dx}\left( (e^x+1)^{-1} \right) \] \[ = 1 + 2(-1)(e^x+1)^{-2} \cdot e^x \] \[ = 1 - \frac{2e^x}{(e^x+1)^2} \] \[ = \frac{(e^x+1)^2 - 2e^x}{(e^x+1)^2} \] \[ = \frac{e^{2x} + 2e^x + 1 - 2e^x}{(e^x+1)^2} \] \[ = \frac{e^{2x} + 1}{(e^x+1)^2} \]che è positiva per ogni valore di \( x \): quindi \( f(x) \) è sempre crescente e perciò, per ogni valore di \( m \), si annulla solo una volta.
Posto \( f(\alpha)=3 \), dobbiamo trovare \( m \) in modo che risulti \( f(-\alpha)=-m \).
Ricordiamo che \( f(x)+f(-x) = 2\ln(4)+2 \). Sostituendo \( x=\alpha \), abbiamo:
\[ f(\alpha)+f(-\alpha) = 2\ln(4)+2 \]Sappiamo che \( f(\alpha)=3 \), quindi:
\[ 3+f(-\alpha) = 2\ln(4)+2 \] \[ f(-\alpha) = 2\ln(4)+2-3 \] \[ f(-\alpha) = 2\ln(4)-1 \]Affinché \( -\alpha \) sia soluzione dell'equazione \( f(x)=-m \), deve essere \( f(-\alpha)=-m \).
Quindi:
\[ -m = 2\ln(4)-1 \] \[ m = -(2\ln(4)-1) \] \[ m = 1-2\ln(4) \]Questo è il valore di \( m \) richiesto.
3)
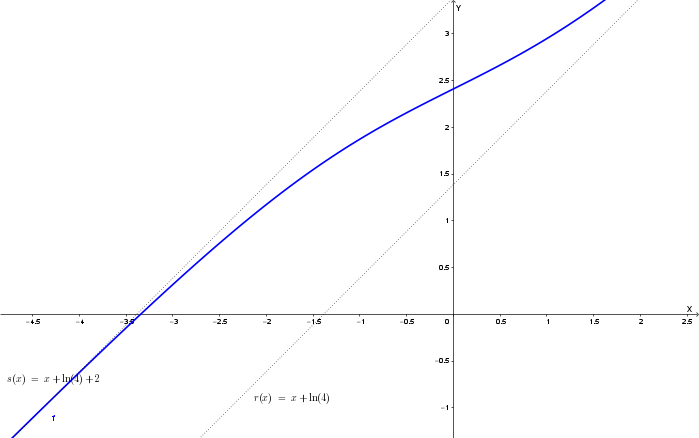
Si provi che, per tutti \( x \) reali, \( f(x)=x+2+\ln(4)-\frac{2e^x}{e^x+1} \). Si provi altresì che la retta \( r \) di equazione \( y=x+\ln(4) \) e la retta \( s \) di equazione \( y=x+2+\ln(4) \) sono asintoti di \( \Gamma \) e che \( \Gamma \) è interamente compresa nella striscia piana delimitata da \( r \) e da \( s \).
Verifichiamo che \( f(x)=x+2+\ln(4)-\frac{2e^x}{e^x+1} \), cioè che:
\[ x+\ln(4)+\frac{2}{e^x+1} = x+2+\ln(4)-\frac{2e^x}{e^x+1} \]che equivale a:
\[ \frac{2}{e^x+1} = 2-\frac{2e^x}{e^x+1} \]Si verifica immediatamente che il secondo membro, riducendo ad una frazione unica, coincide con il primo membro:
\[ 2-\frac{2e^x}{e^x+1} = \frac{2(e^x+1) - 2e^x}{e^x+1} = \frac{2e^x+2-2e^x}{e^x+1} = \frac{2}{e^x+1} \]L'identità è provata.
Verifica dell'asintoto obliquo \( r: y=x+\ln(4) \) per \( x \to +\infty \)
Calcoliamo il coefficiente angolare \( m \):
\[ m = \lim_{x \to +\infty} \frac{f(x)}{x} = \lim_{x \to +\infty} \frac{x+\ln(4)+\frac{2}{e^x+1}}{x} \] \[ = \lim_{x \to +\infty} \left( 1 + \frac{\ln(4)}{x} + \frac{2}{x(e^x+1)} \right) = 1 + 0 + 0 = 1 \]Calcoliamo il termine noto \( q \):
\[ q = \lim_{x \to +\infty} (f(x) - mx) = \lim_{x \to +\infty} (f(x) - x) \] \[ = \lim_{x \to +\infty} \left( x+\ln(4)+\frac{2}{e^x+1} - x \right) = \lim_{x \to +\infty} \left( \ln(4)+\frac{2}{e^x+1} \right) = \ln(4)+0 = \ln(4) \]Poiché \( m=1 \) e \( q=\ln(4) \), la retta \( r: y=x+\ln(4) \) è un asintoto obliquo per \( x \to +\infty \).
Verifica dell'asintoto obliquo \( s: y=x+2+\ln(4) \) per \( x \to -\infty \)
Utilizziamo la forma alternativa di \( f(x) \): \( f(x)=x+2+\ln(4)-\frac{2e^x}{e^x+1} \).
Calcoliamo il coefficiente angolare \( m \):
\[ m = \lim_{x \to -\infty} \frac{f(x)}{x} = \lim_{x \to -\infty} \frac{x+2+\ln(4)-\frac{2e^x}{e^x+1}}{x} \] \[ = \lim_{x \to -\infty} \left( 1 + \frac{2+\ln(4)}{x} - \frac{2e^x}{x(e^x+1)} \right) = 1 + 0 - 0 = 1 \]Calcoliamo il termine noto \( q \):
\[ q = \lim_{x \to -\infty} (f(x) - mx) = \lim_{x \to -\infty} (f(x) - x) \] \[ = \lim_{x \to -\infty} \left( 2+\ln(4)-\frac{2e^x}{e^x+1} \right) \] \[ = 2+\ln(4) - \frac{2 \cdot 0}{0+1} = 2+\ln(4) - 0 = 2+\ln(4) \]Poiché \( m=1 \) e \( q=2+\ln(4) \), la retta \( s: y=x+2+\ln(4) \) è un asintoto obliquo per \( x \to -\infty \).
Risulta poi, per ogni \( x \), la differenza tra la funzione e l'asintoto \( r \) è \( f(x) - (x+\ln(4)) = \frac{2}{e^x+1} \), che è sempre maggiore di zero (\( \frac{2}{e^x+1} > 0 \)).
Questo significa che la curva \( \Gamma \) è sempre al di sopra della retta \( r \).
Inoltre, la differenza tra la funzione e l'asintoto \( s \) è \( f(x) - (x+2+\ln(4)) = -\frac{2e^x}{e^x+1} \), e dato che \( e^x > 0 \) per ogni \( x \), allora \( -\frac{2e^x}{e^x+1} \) è sempre minore di zero.
Questo significa che la curva \( \Gamma \) è sempre al di sotto della retta \( s \).
Pertanto la curva \( \Gamma \) è compresa nella striscia piana delimitata dalle rette \( r \) ed \( s \).
4)
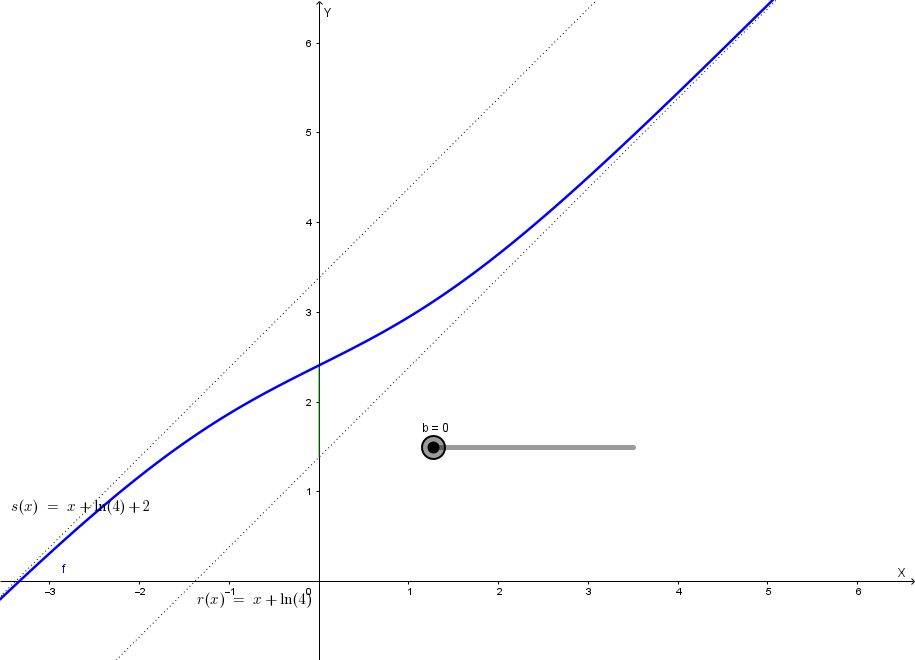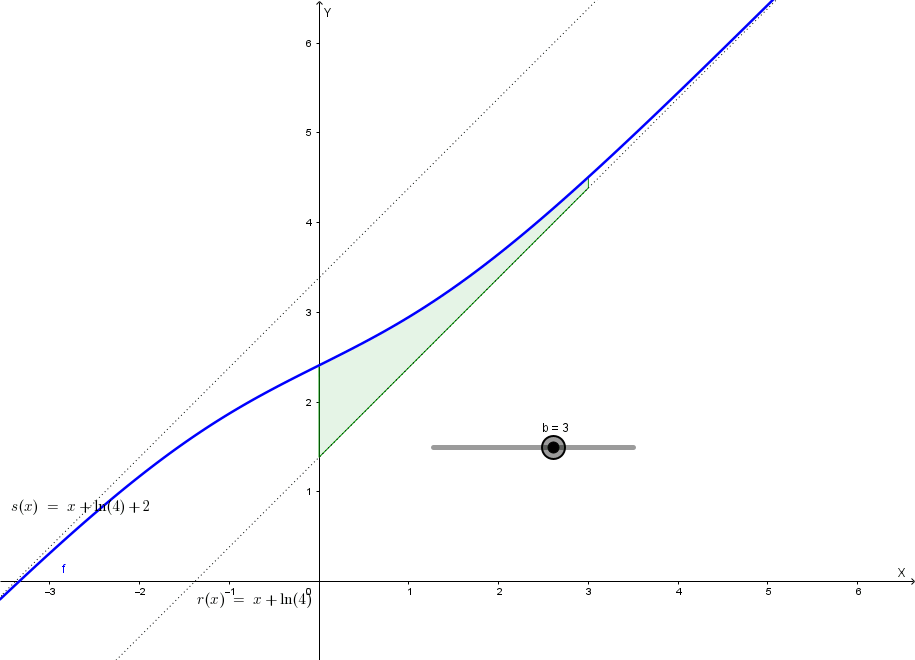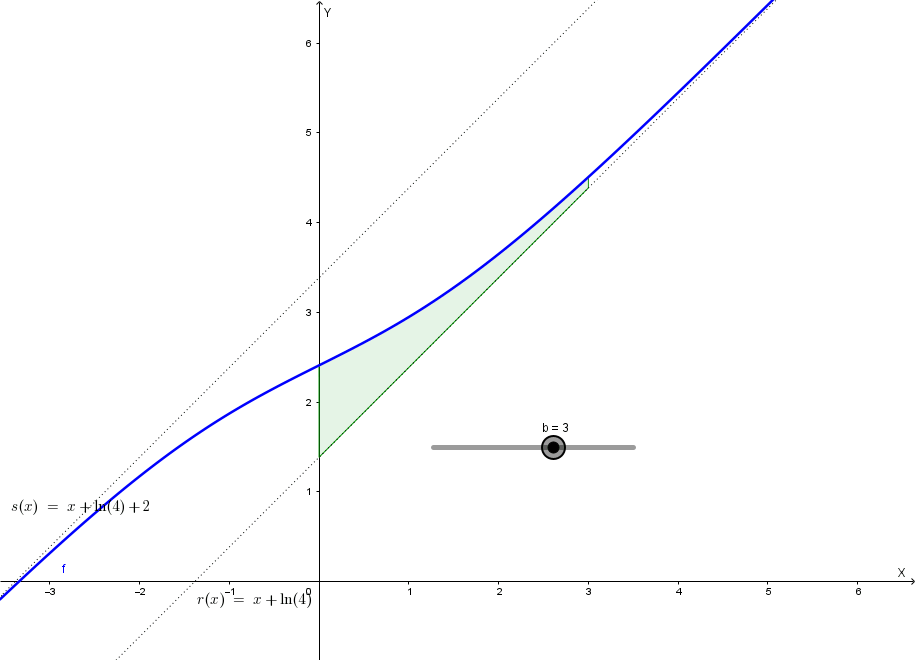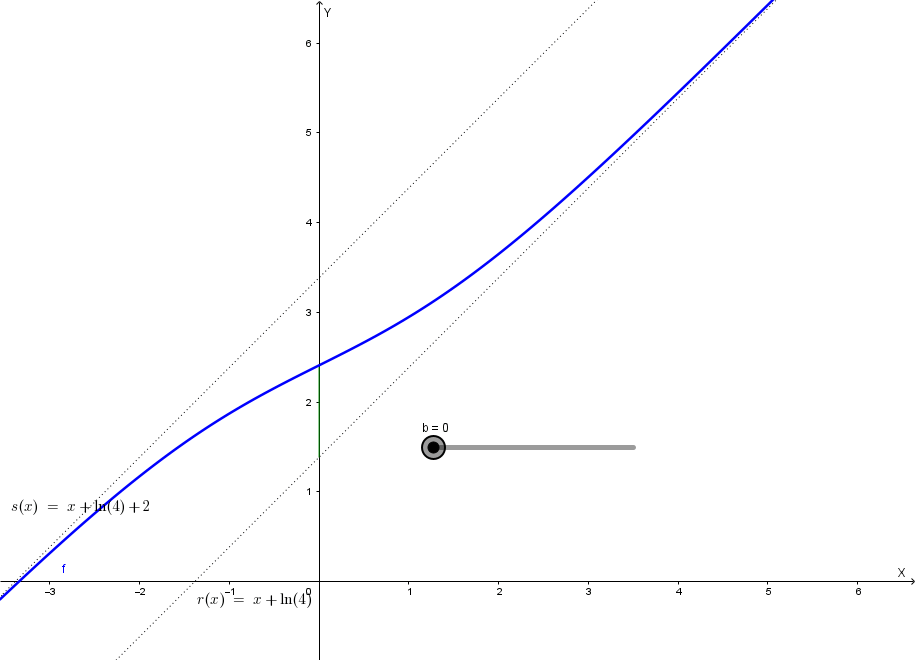
Posto \( I(\beta)=\int_0^\beta [f(x)-x-\ln(4)] dx \), si calcoli il limite per \( \beta \to +\infty \) di \( I(\beta) \). Qual è il significato geometrico ottenuto?
Innanzitutto, semplifichiamo l'integranda:
\[ f(x)-x-\ln(4) = \left( x+\ln(4)+\frac{2}{e^x+1} \right) - x - \ln(4) = \frac{2}{e^x+1} \]Quindi, l'integrale diventa:
\[ I(\beta) = \int_0^\beta \frac{2}{e^x+1} dx \]Calcoliamo l'integrale indefinito della funzione \( \frac{2}{e^x+1} \):
\[ \int \frac{2}{e^x+1} dx \]Possiamo riscrivere l'integranda manipolando il numeratore:
\[ \frac{2}{e^x+1} = \frac{2(e^x+1-e^x)}{e^x+1} = \frac{2(e^x+1)}{e^x+1} - \frac{2e^x}{e^x+1} = 2 - \frac{2e^x}{e^x+1} \]Ora integriamo termine per termine:
\[ \int \left( 2 - \frac{2e^x}{e^x+1} \right) dx = \int 2 dx - \int \frac{2e^x}{e^x+1} dx \]Il primo integrale è semplice: \( \int 2 dx = 2x \).
Per il secondo integrale, notiamo che \( 2e^x \) è la derivata di \( 2(e^x+1) \), oppure \( \frac{2e^x}{e^x+1} \) è della forma \( k \cdot \frac{f'(x)}{f(x)} \), il cui integrale è \( k \ln|f(x)| \). Poiché \( e^x+1 \) è sempre positivo, possiamo omettere il valore assoluto:
\[ \int \frac{2e^x}{e^x+1} dx = 2\ln(e^x+1) \]Quindi, l'integrale indefinito è:
\[ \int \frac{2}{e^x+1} dx = 2x - 2\ln(e^x+1) + C \]Applicando gli estremi di integrazione per calcolare \( I(\beta) \):
\[ I(\beta) = \left[ 2x - 2\ln(e^x+1) \right]_0^\beta \] \[ = (2\beta - 2\ln(e^\beta+1)) - (2 \cdot 0 - 2\ln(e^0+1)) \] \[ = 2\beta - 2\ln(e^\beta+1) + 2\ln(2) \]Ora calcoliamo il limite per \( \beta \to +\infty \) di \( I(\beta) \):
\[ \lim_{\beta \to +\infty} I(\beta) = \lim_{\beta \to +\infty} [2\beta - 2\ln(e^\beta+1) + 2\ln(2)] \]Raccogliamo \( e^\beta \) all'interno del logaritmo:
\[ = \lim_{\beta \to +\infty} [2\beta - 2\ln(e^\beta(1+e^{-\beta})) + 2\ln(2)] \]Applichiamo la proprietà dei logaritmi \( \ln(ab) = \ln(a) + \ln(b) \):
\[ = \lim_{\beta \to +\infty} [2\beta - 2(\ln(e^\beta) + \ln(1+e^{-\beta})) + 2\ln(2)] \] \[ = \lim_{\beta \to +\infty} [2\beta - 2(\beta + \ln(1+e^{-\beta})) + 2\ln(2)] \] \[ = \lim_{\beta \to +\infty} [2\beta - 2\beta - 2\ln(1+e^{-\beta}) + 2\ln(2)] \] \[ = \lim_{\beta \to +\infty} [-2\ln(1+e^{-\beta}) + 2\ln(2)] \]Poiché \( \lim_{\beta \to +\infty} e^{-\beta} = 0 \), allora \( \lim_{\beta \to +\infty} (1+e^{-\beta}) = 1 \), e \( \lim_{\beta \to +\infty} \ln(1+e^{-\beta}) = \ln(1) = 0 \).
Quindi:
\[ \lim_{\beta \to +\infty} I(\beta) = -2(0) + 2\ln(2) = 2\ln(2) = \ln(2^2) = \ln(4) \]Questo limite tende a \( \ln(4) \) per \( \beta \to +\infty \).
Significato geometrico
Il significato geometrico del limite trovato è l'**area della regione illimitata** compresa tra il grafico di \( f(x) \) e la sua retta asintotica \( r: y=x+\ln(4) \) per \( x \geq 0 \).
Infatti, l'integranda è \( f(x)-x-\ln(4) \), che rappresenta la distanza verticale (con segno) tra la curva \( \Gamma \) e l'asintoto obliquo \( r \).
Poiché \( f(x) - (x+\ln(4)) = \frac{2}{e^x+1} \), che è sempre maggiore di zero (\( > 0 \)), la curva \( \Gamma \) sta sempre al di sopra dell'asintoto \( r \).
Quindi, \( \ln(4) \) rappresenta l'area della regione illimitata che si estende da \( x=0 \) a \( +\infty \), delimitata dalla curva \( \Gamma \) e dalla retta \( r \).