

Risolvi da solo i vari punti del problema e controlla le soluzioni premendo (una o due volte) il tasto corrispondente.
1)
Verifica che nei punti \(x=1\) e \(x=-1\) le funzioni \(g_1, g_2, g_3, g_4\) condividono le stesse rette tangenti.
Calcoliamo le derivate delle funzioni:
\[ g_1'(x) = x \] \[ g_2'(x) = \begin{cases} 1 & \text{se } x > 0 \\ -1 & \text{se } x < 0 \end{cases} \] \[ g_3'(x) = \sin\left(\frac{\pi}{2}x\right) \] \[ g_4'(x) = \frac{1}{x} \]Cerchiamo i valori che tali derivate assumono in \(x=1\) e \(x=-1\), che equivalgono ai coefficienti angolari delle rette tangenti:
\[ g_1'(1) = 1, \quad g_2'(1) = 1, \quad g_3'(1) = 1, \quad g_4'(1) = 1 \] \[ g_1'(-1) = -1, \quad g_2'(-1) = -1, \quad g_3'(-1) = -1, \quad g_4'(-1) = -1 \]Calcoliamo i valori che assumono le funzioni in \(x=1\) e \(x=-1\):
\[ g_1(1) = 0, \quad g_2(1) = 0, \quad g_3(1) = 0, \quad g_4(1) = 0 \] \[ g_1(-1) = 0, \quad g_2(-1) = 0, \quad g_3(-1) = 0, \quad g_4(-1) = 0 \]Le tangenti in \((1; 0)\) hanno coefficiente angolare 1, quindi equazione: \(y = x - 1\)
Le tangenti in \((-1; 0)\) hanno coefficiente angolare -1, quindi equazione: \(y = -x - 1\)
2)
Dopo aver tracciato i grafici delle funzioni \(g_1, g_2, g_3, g_4\) deduci quelli delle funzioni:
\[ f_1(x) = \begin{cases} \ln|x| & \text{se } |x| \ge 1 \\ -g_1(x) & \text{se } |x| < 1 \end{cases} \] \[ f_2(x) = \begin{cases} \ln|x| & \text{se } |x| \ge 1 \\ -g_2(x) & \text{se } |x| < 1 \end{cases} \] \[ f_3(x) = \begin{cases} \ln|x| & \text{se } |x| \ge 1 \\ -g_3(x) & \text{se } |x| < 1 \end{cases} \]Classifica gli eventuali punti di non derivabilità di \(f_1, f_2, f_3\) e posto:
\[ I_1 = \int_{-e}^{e} f_1(x) \,dx \] \[ I_2 = \int_{-e}^{e} f_2(x) \,dx \] \[ I_3 = \int_{-e}^{e} f_3(x) \,dx \]verifica le disuguaglianze: \(I_1 < I_3 < I_2\).
Grafici delle funzioni g(x)
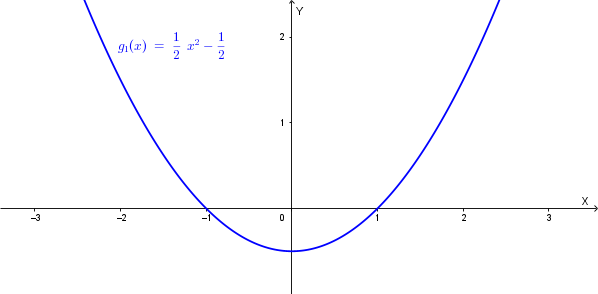
Il grafico di \(g_1(x) = \frac{1}{2}x^2 - \frac{1}{2}\) è una parabola con vertice in \((0; -\frac{1}{2})\), asse di simmetria l'asse \(y\) e concavità verso l'alto.
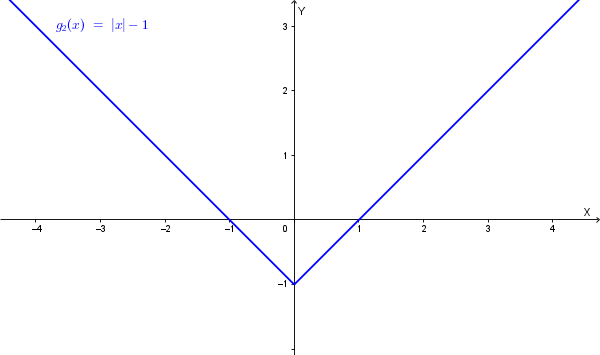
Il grafico di \(g_2(x) = |x| - 1\) si ottiene da \(y=|x|\) traslando verso il basso di 1.
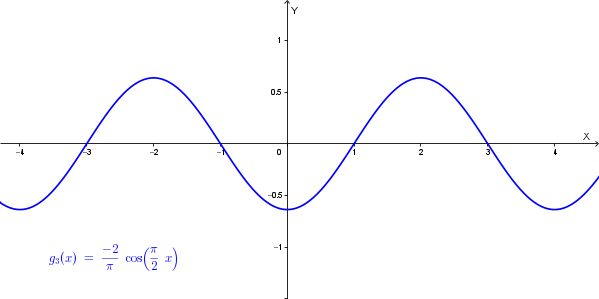
Il grafico di \(g_3(x) = -\frac{2}{\pi}\cos\left(\frac{\pi}{2}x\right)\) è una funzione coseno con periodo \(T = \frac{2\pi}{\frac{\pi}{2}} = 4\) e situata tra \(-\frac{2}{\pi}\) e \(\frac{2}{\pi}\).
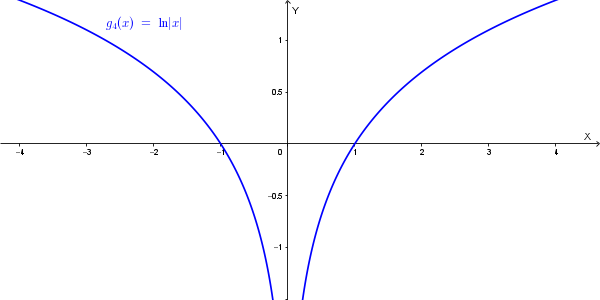
Il grafico di \(g_4(x) = \ln(|x|)\) si ottiene da \(\ln(x)\) con l'aggiunta della sua simmetrica rispetto all'asse \(y\).
Grafici delle funzioni f(x)
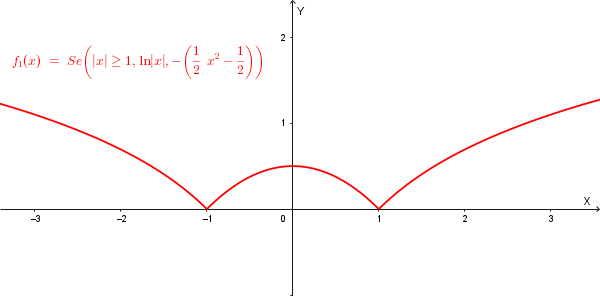
Il grafico di \(f_1(x) = \begin{cases} \ln|x| & \text{se } |x| \ge 1 \\ -g_1(x) & \text{se } |x| < 1 \end{cases}\) è il seguente:
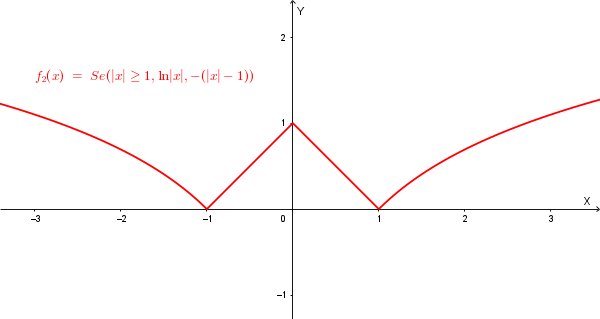
Il grafico di \(f_2(x) = \begin{cases} \ln|x| & \text{se } |x| \ge 1 \\ -g_2(x) & \text{se } |x| < 1 \end{cases}\) è il seguente:
Il grafico di \(f_3(x) = \begin{cases} \ln|x| & \text{se } |x| \ge 1 \\ -g_3(x) & \text{se } |x| < 1 \end{cases}\) è il seguente:
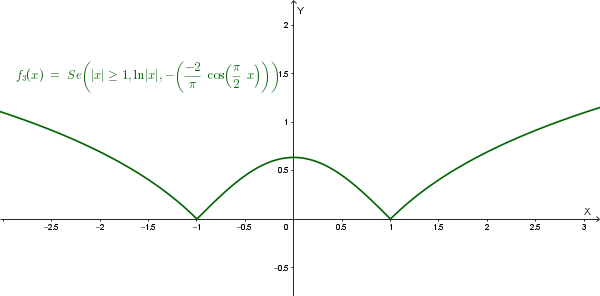
Le tre funzioni hanno in \(x=-1\) e \(x=1\) dei punti angolosi; inoltre la funzione \(f_2\) ha un altro punto angoloso in \(x=0\).
Posto:
\[ I_1 = \int_{-e}^{e} f_1(x) \,dx \] \[ I_2 = \int_{-e}^{e} f_2(x) \,dx \] \[ I_3 = \int_{-e}^{e} f_3(x) \,dx \]Verifichiamo le disuguaglianze: \(I_1 < I_3 < I_2\).
Osserviamo il seguente grafico:
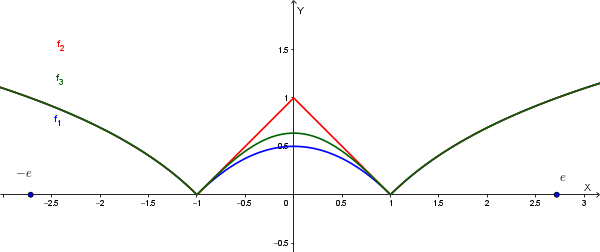
La dimostrazione della proprietà richiesta segue dal fatto che per \(|x|>1\) le tre funzioni coincidono e nell'intervallo \([-1; 1]\) risulta:
\[ f_1 < f_3 < f_2 \]3)
Posto:
\[ h(x) = \begin{cases} 0 & \text{se } x \le 0 \\ g_1(x) & \text{se } 0 < x < 1 \\ \ln(|x|) & \text{se } x \ge 1 \end{cases} \]Dimostra che la funzione: \(H(x) = \int_0^x h(t) \,dt\) ammette uno zero nell'intervallo \([\sqrt{e}; e]\).
Osserviamo il grafico di \(h(x)\):
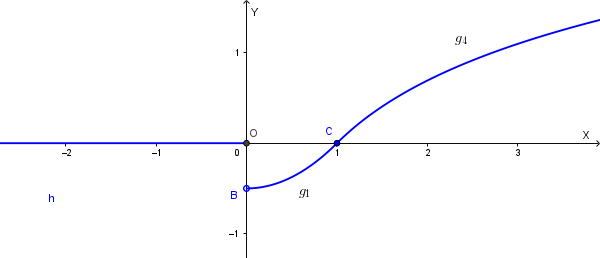
Lo zero richiesto è il punto \(a>1\) tale che:
\[ \int_1^a \ln(x) \,dx = - \int_0^1 \left(\frac{1}{2}x^2 - \frac{1}{2}\right) \,dx \] \[ = -\left[\frac{1}{6}x^3 - \frac{1}{2}x\right]_0^1 \] \[ = -\left[\frac{1}{6} - \frac{1}{2}\right] = -\left[\frac{1 - 3}{6}\right] = -\left[-\frac{2}{6}\right] = \frac{1}{3} \]Determiniamo per parti una primitiva di \(\ln(x)\):
\[ \int \ln(x) \,dx = x\ln(x) - \int x \cdot \frac{1}{x} \,dx = x\ln(x) - x + C \]Quindi:
\[ \int_1^a \ln(x) \,dx = [x\ln(x) - x]_1^a = a\ln a - a + 1 = \frac{1}{3} \]da cui: \(\ln a = \frac{a-2}{3a}\)
Con \(a=\sqrt{e}\) si ha:
\(\ln a = \ln\sqrt{e} = \frac{1}{2}\)
e
\(\frac{a-2}{3a} = \frac{\sqrt{e}-2}{3\sqrt{e}} \approx 0.6 > \frac{1}{2}\)
Con \(a=e\) si ha:
\(\ln a = \ln e = 1\)
e
\(\frac{a-2}{3a} = \frac{e-2}{3e} \approx 0.8 < 1\)
Quindi: \(\sqrt{e} < a < e\)
4)
Calcola il volume del solido ottenuto facendo ruotare di \(\frac{\pi}{3}\) radianti intorno all'asse \(x\) la regione di piano delimitata dalle rette di equazioni \(x=-1\), \(x=+1\) e dai grafici di \(g_2\) e \(g_1\).
Rappresentiamo la regione R richiesta:
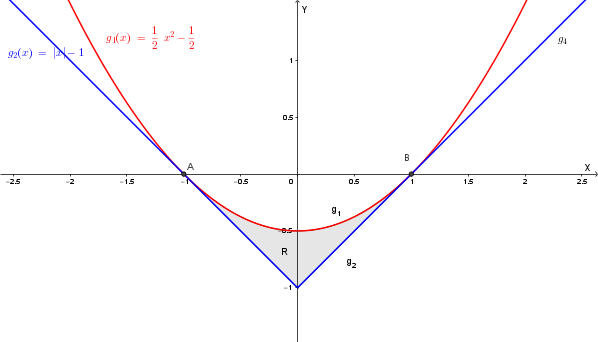
Ricordiamo che il volume del solido ottenuto dalla rotazione di \(2\pi\) della regione di piano compresa fra il grafico di una funzione \(f(x)\) e le rette \(x=a\) e \(x=b\) intorno all'asse \(x\) è dato da:
\[ V = \pi \int_a^b f^2(x) \,dx \]Se la rotazione è di \(\alpha\) radianti il volume \(V'\) si ottiene a partire dalla seguente proporzione:
\[ \frac{V'}{V} = \frac{\alpha}{2\pi} \]quindi:
\[ V' = \frac{\alpha}{2\pi} V = \frac{\alpha}{2} \int_a^b f^2(x) \,dx \]Se la rotazione è quella della regione compresa fra i grafici delle due funzioni \(f(x)\) e \(g(x)\), supponendo \(f\) e \(g\) positive e \(f(x) > g(x)\) si ha:
\[ V = \frac{\alpha}{2} \int_a^b [f^2(x) - g^2(x)] \,dx \]Nel nostro caso dobbiamo calcolare il volume del solido generato dalla rotazione di \(\frac{\pi}{3}\) radianti della regione delimitata dai grafici di \(g_1(x)\) e \(g_2(x)\) e dalle rette \(x=-1\) e \(x=1\).
Le funzioni \(g_1(x) = \frac{1}{2}x^2 - \frac{1}{2}\) e \(g_2(x) = |x| - 1\) sono entrambe pari, quindi l'integrale sull'intervallo \([-1, 1]\) può essere calcolato come il doppio dell'integrale su \([0, 1]\). In questo intervallo, \(|x|=x\), quindi \(g_2(x) = x-1\).
Nell'intervallo \([0, 1]\), \(g_1(x) = \frac{1}{2}x^2 - \frac{1}{2}\) va da \(-\frac{1}{2}\) a \(0\), mentre \(g_2(x) = x-1\) va da \(-1\) a \(0\). In questo intervallo, si verifica che \(g_1(x) \ge g_2(x)\). Pertanto, la formula per il volume del solido di rotazione della regione tra le due curve è data da \(\frac{\alpha}{2} \int_a^b [g_1^2(x) - g_2^2(x)] \,dx\).
\[ V = 2\left[ \frac{\pi}{3} \cdot \frac{1}{2} \int_0^1 (g_1^2(x) - g_2^2(x)) \,dx \right] \] \[ = \frac{\pi}{3} \int_0^1 \left[\left(\frac{1}{2}x^2 - \frac{1}{2}\right)^2 - (x-1)^2\right] \,dx \] \[ = \frac{\pi}{3} \int_0^1 \left[\left(\frac{1}{4}x^4 - \frac{1}{2}x^2 + \frac{1}{4}\right) - (x^2 - 2x + 1)\right] \,dx \] \[ = \frac{\pi}{3} \int_0^1 \left(\frac{1}{4}x^4 - \frac{3}{2}x^2 + 2x - \frac{3}{4}\right) \,dx \] \[ = \frac{\pi}{3} \left[\frac{1}{20}x^5 - \frac{1}{2}x^3 + x^2 - \frac{3}{4}x\right]_0^1 \] \[ = \frac{\pi}{3} \left(\frac{1}{20} - \frac{1}{2} + 1 - \frac{3}{4}\right) \] \[ = \frac{\pi}{3} \left(\frac{1 - 10 + 20 - 15}{20}\right) = \frac{\pi}{3} \left(-\frac{4}{20}\right) = -\frac{\pi}{15} \]Poiché il volume deve essere positivo, prendiamo il valore assoluto del risultato.
\[ V = \frac{\pi}{15} \]