Soluzione del punto 1

Calcoliamo le derivate della funzione \(f(x) = \ln(ae^{bx}+c)\), con \(a, b, c\) parametri reali positivi:

\[f'(x) = \frac{abe^{bx}}{ae^{bx}+c} > 0 \quad \forall x \in \mathbb{R} \quad \text{perché } a, b, c \text{ sono positivi}\]

Calcoliamo la derivata seconda:

\[f''(x) = \frac{ab^2e^{bx}(ae^{bx}+c) - abe^{bx}(abe^{bx})}{(ae^{bx}+c)^2} = \frac{ab^2e^{bx}(ae^{bx}+c-ae^{bx})}{(ae^{bx}+c)^2} = \frac{ab^2ce^{bx}}{(ae^{bx}+c)^2}\]

e risulta \(f''(x) > 0 \quad \forall x \in \mathbb{R}\) perché \(a, b, c\) sono positivi.

Soluzione del punto 2

Verifichiamo la presenza dell'asintoto orizzontale per \(x \to -\infty\):

\[\lim_{x \to -\infty}(\ln(ae^{bx}+c)) = \ln(c)\]

quindi \(f\) ha l'asintoto orizzontale \(y=\ln(c)\) per \(x \to -\infty\). Per avere \(y=0\), dobbiamo porre \(\ln(c)=0\), il che implica \(c=1\).

Verifichiamo ora che \(f\) ha un asintoto obliquo per \(x \to +\infty\):

Calcoliamo il coefficiente angolare \(m\):

\[m = \lim_{x \to +\infty}\left(\frac{\ln(ae^{bx}+c)}{x}\right) = \lim_{x \to +\infty}\left(\frac{\ln(ae^{bx})}{x}\right) = \lim_{x \to +\infty}\left(\frac{\ln(a)+\ln(e^{bx})}{x}\right) =\] \[= \lim_{x \to +\infty}\left(\frac{\ln(a)+bx}{x}\right) = \lim_{x \to +\infty}\left(\frac{bx}{x}\right) = b\]

Quindi \(m=b\).

Calcoliamo il termine noto \(q\):

\[q = \lim_{x \to +\infty}(f(x)-mx) = \lim_{x \to +\infty}(\ln(ae^{bx}+c)-bx) = \lim_{x \to +\infty}\left(\ln\left(e^{bx}\left(a+\frac{c}{e^{bx}}\right)\right)-bx\right) =\] \[= \lim_{x \to +\infty}\left(\ln(e^{bx})+\ln\left(a+\frac{c}{e^{bx}}\right)-bx\right) = \lim_{x \to +\infty}\left(bx+\ln\left(a+\frac{c}{e^{bx}}\right)-bx\right) =\] \[= \lim_{x \to +\infty}\ln\left(a+\frac{c}{e^{bx}}\right) = \ln(a+0) = \ln(a)\]

Quindi \(q=\ln(a)\).

La funzione, per \(x \to +\infty\), ha l'asintoto obliquo \(y=bx+\ln(a)\) che coincide con \(y=x\) se \(b=1\) ed \(a=1\).

Soluzione del punto 3

Con \(a=b=c=1\) la funzione diventa: \(f(x)=\ln(e^x+1)\).

Osserviamo che:

\[\ln(e^x+1) > \ln(e^x) = x\]

quindi \(f(x) > x\).

Per verificare che \(f(x) < e^x\), studiamo qualitativamente la funzione \(y=f(x)=\ln(e^x+1)\):

• La funzione è definita su tutto \(\mathbb{R}\).
• Per \(x=0\), \(f(0) = \ln(e^0+1) = \ln(1+1) = \ln(2)\).
• Per \(y=0\), \( \ln(e^x+1) = 0 \implies e^x+1 = e^0 \implies e^x+1 = 1 \implies e^x = 0 \), che non ha soluzioni (mai).
• La funzione è positiva quando \(e^x+1 > 1 \implies e^x > 0\), il che è sempre vero per ogni \(x \in \mathbb{R}\).

Calcolo dei limiti:

• Se \(x \to -\infty\), \(f(x) = \ln(e^x+1) \to \ln(0+1) = \ln(1) = 0^+\). Quindi \(y=0\) è un asintoto orizzontale per \(x \to -\infty\) (come visto nel punto precedente).
• Se \(x \to +\infty\), \(f(x) = \ln(e^x+1) \to +\infty\). È possibile un asintoto obliquo. Dai risultati del punto 2, con \(a=1\) e \(b=1\), l'asintoto obliquo per \(x \to +\infty\) è \(y=1x+\ln(1) \implies y=x\).

Monotonia e Concavità:

• Monotonia: \(f'(x) > 0 \quad \forall x \in \mathbb{R}\), come dimostrato nel punto 1: la funzione è sempre crescente.
• Concavità: \(f''(x) > 0 \quad \forall x \in \mathbb{R}\), come dimostrato nel punto 1: la concavità è sempre verso l'alto, nessun flesso.

Il grafico è quindi il seguente:

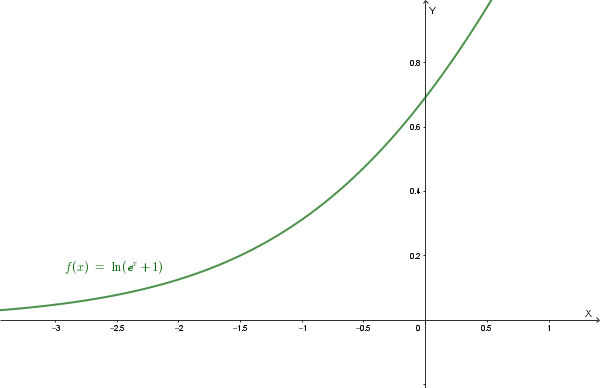
Rappresentando nello stesso piano cartesiano le tre funzioni \(y=x\), \(y=f(x)\) e \(y=e^x\) si può constatare che \(x < f(x) < e^x \quad \forall x \in \mathbb{R}\):

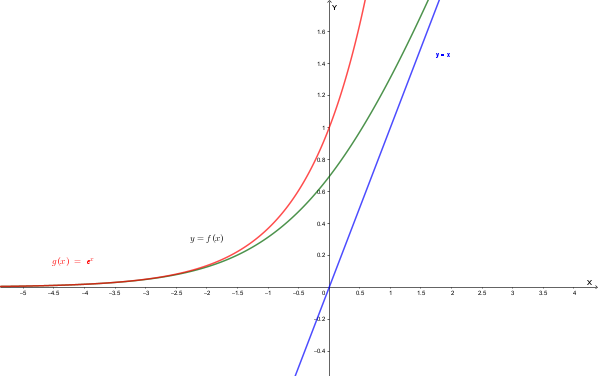
Osserviamo che per \(x=0\), \(f(x) < e^x\) in quanto \(\ln(2) < 1\). Inoltre, per \(x \to -\infty\), \(f(x)\) ed \(e^x\) sono infinitesimi dello stesso ordine, essendo:

\[\lim_{x \to -\infty}\frac{\ln(e^x+1)}{e^x} = \lim_{x \to -\infty}\frac{e^x}{e^x} = 1 \quad (\text{N.B. Siccome } e^x \to 0 \text{, } \ln(e^x+1) \sim e^x)\]

Soluzione del punto 4

Il grafico di \(h(x)=f(-|x|)\) si ottiene dal grafico di \(f(x)\) con le seguenti trasformazioni:

1. Riflessione rispetto all'asse y: \(y=f(x) \to y=f(-x)\)

Questa trasformazione produce una simmetria rispetto all'asse delle \(y\).

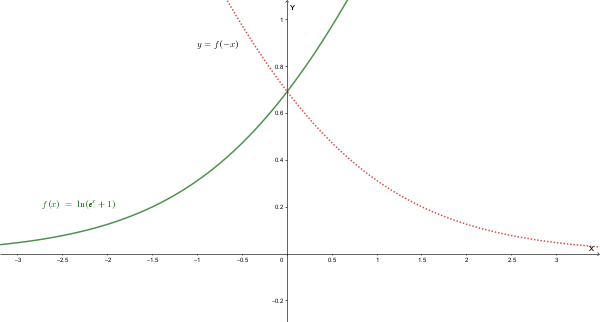
2. Trasformazione in \(y=f(-|x|)=h(x)\)

Si prende il grafico di \(f(-x)\) che si trova a destra dell'asse \(y\) (cioè per \(x \ge 0\)) e lo si ribalta simmetricamente a sinistra (per \(x < 0\)).

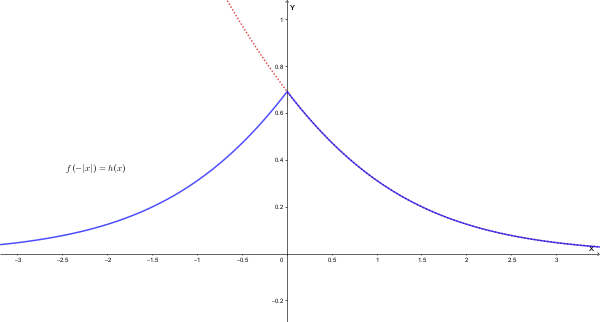
Per dimostrare che \(A<2\) è sufficiente dimostrare che:

\[\int_{-\infty}^{0} f(x) \,dx < 1\]

ma ricordiamo che \(f(x) < e^x\) per ogni \(x \in \mathbb{R}\) (dimostrato nel punto 3). Quindi:

\[\int_{-\infty}^{0} f(x) \,dx < \int_{-\infty}^{0} e^x \,dx\]

Calcoliamo l'integrale del membro di destra:

\[\int_{-\infty}^{0} e^x \,dx = \lim_{k \to -\infty}\int_{k}^{0} e^x \,dx = \lim_{k \to -\infty}[e^x]_{k}^{0} = \lim_{k \to -\infty}(e^0 - e^k) = \lim_{k \to -\infty}(1 - e^k) = 1 - 0 = 1\]

Quindi, abbiamo \(\int_{-\infty}^{0} f(x) \,dx < 1\). Poiché il grafico di \(h(x)\) è simmetrico rispetto all'asse \(y\), l'area totale \(A\) è il doppio dell'area sotto \(f(x)\) da \(-\infty\) a \(0\):

\[A = 2 \int_{-\infty}^{0} f(x) \,dx\]

Da cui, \(A < 2 \cdot 1 = 2\). Questo dimostra che \(A < 2\).

Cerchiamo infine un numero reale \(S\), quanto più grande possibile, tale che \(A>S\).

A tal fine determiniamo l'area \(S\) del triangolo \(ABC\) formato dalle tangenti (destra e sinistra) al grafico di \(h(x)\) nel punto angoloso \(C=(0; \ln(2))\).

Per \(x<0\), \(h(x) = f(-(-x)) = f(x) = \ln(e^x+1)\). La derivata è \(h'(x) = \frac{e^x}{e^x+1}\).

La semi-tangente sinistra in \(C=(0, \ln(2))\) ha pendenza \(h'_{-}(0) = \frac{e^0}{e^0+1} = \frac{1}{1+1} = \frac{1}{2}\).

L'equazione della semi-tangente sinistra è: \(y - \ln(2) = \frac{1}{2}x\).

Questa retta interseca l'asse \(x\) (\(y=0\)) quando \(-\ln(2) = \frac{1}{2}x \implies x = -2\ln(2)\). Questo è il punto \(A = (-2\ln(2), 0)\).

Per \(x>0\), \(h(x) = f(-x) = \ln(e^{-x}+1)\). La derivata è \(h'(x) = \frac{-e^{-x}}{e^{-x}+1}\).

La semi-tangente destra in \(C=(0, \ln(2))\) ha pendenza \(h'_{+}(0) = \frac{-e^0}{e^0+1} = \frac{-1}{1+1} = -\frac{1}{2}\).

L'equazione della semi-tangente destra è: \(y - \ln(2) = -\frac{1}{2}x\).

Questa retta interseca l'asse \(x\) (\(y=0\)) quando \(-\ln(2) = -\frac{1}{2}x \implies x = 2\ln(2)\). Questo è il punto \(B = (2\ln(2), 0)\).

Il triangolo \(ABC\) ha base \(AB = 2\ln(2) - (-2\ln(2)) = 4\ln(2)\) e altezza pari all'ordinata di \(C\), che è \(\ln(2)\).

L'area \(S\) del triangolo \(ABC\) è:

\[S = \text{Area}(ABC) = \frac{1}{2} \cdot \text{base} \cdot \text{altezza} = \frac{1}{2} \cdot 4\ln(2) \cdot \ln(2) = 2\ln^2(2)\]

Calcoliamo il valore numerico: \(S = 2 \cdot (\ln(2))^2 \approx 2 \cdot (0.6931)^2 \approx 2 \cdot 0.4805 = 0.961\).

Il grafico che illustra questo triangolo è il seguente:

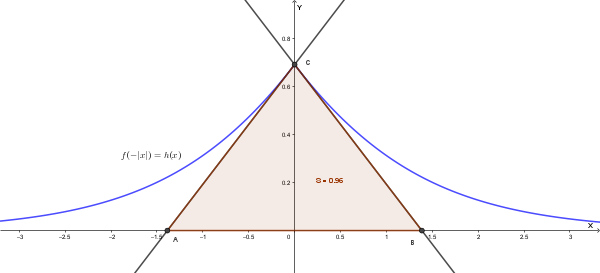
Quindi il numero reale \(S\) (quanto più grande possibile) tale che \(A>S\) è \(S=2\ln^2(2) \approx 0.96\).