Soluzione del punto 1

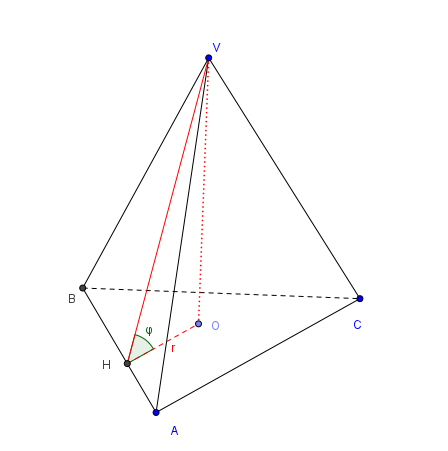
Posto \(BC=x\), risulta:

\[AB=\frac{3}{5}x\] \[AC=\sqrt{BC^2-AB^2}=\sqrt{x^2-\left(\frac{3}{5}x\right)^2}=\sqrt{x^2-\frac{9}{25}x^2}=\sqrt{\frac{16}{25}x^2}=\frac{4}{5}x\]

L’area del triangolo rettangolo ABC di cateti AB e AC è:

\[A(ABC)=\frac{AB \cdot AC}{2}=\frac{1}{2}\left(\frac{3}{5}x\right)\left(\frac{4}{5}x\right)=\frac{6}{25}x^2=24a^2\]

Da cui:

\[x^2=\frac{24 \cdot 25}{6}a^2=100a^2 \implies x=10a\]

I lati di ABC misurano quindi:

\[AB=6a, \quad AC=8a, \quad BC=10a\]

Indichiamo con \(r\) la distanza \(OH\) del piede \(O\) dell’altezza della piramide dal cateto \(AB\) e, osservato che \(O\) è il centro della circonferenza inscritta nel triangolo ABC (per definizione di piramide retta), \(r\) è il raggio della circonferenza inscritta nel triangolo ABC.

Ricordiamo che, detto \(p\) il semiperimetro di un poligono circoscritto ad una circonferenza di raggio \(r\) ed \(A\) l’area del poligono stesso, risulta: \(A=p \cdot r\), da cui:

\[r=\frac{A}{p}=\frac{24a^2}{\frac{1}{2}(6a+8a+10a)}=\frac{24a^2}{12a}=2a\]

Considerando il triangolo VOH, rettangolo in O, essendo VHO una sezione normale del diedro formato dalle facce VAB ed ABC, si ha:

\[VO=OH \cdot \tan\phi = r \cdot \tan\phi = 2a \cdot \tan\phi\]

Dobbiamo determinare \(\tan\phi\) sapendo che \(\sin\phi=\frac{12}{13}\).

Notato che l’angolo \(\phi\) è acuto, otteniamo:

\[\tan\phi=\frac{\sin\phi}{\cos\phi}=\frac{\sin\phi}{\sqrt{1-\sin^2\phi}}=\frac{\frac{12}{13}}{\sqrt{1-\left(\frac{12}{13}\right)^2}}=\frac{\frac{12}{13}}{\sqrt{1-\frac{144}{169}}}=\frac{\frac{12}{13}}{\sqrt{\frac{25}{169}}}=\frac{\frac{12}{13}}{\frac{5}{13}}=\frac{12}{5}\]

Pertanto:

\[VO=2a \cdot \frac{12}{5}=\frac{24}{5}a\]

L’altezza della piramide è \(VO=\frac{24}{5}a\).

Soluzione del punto 2

La distanza di C dal piano della faccia VAB non è altro che l’altezza della piramide relativa alla base ABV. Calcolando il volume della piramide e l’area della base ABV riusciremmo a calcolare l’altezza della piramide relativa alla base ABV.

\[V=\frac{1}{3}Area(ABC)\cdot VO=\frac{1}{3}\cdot 24a^2\cdot \frac{24}{5}a=\frac{192}{5}a^3\]

Per trovare l’area di ABV cerchiamo VH:

\[VH=\frac{r}{\cos\phi}=\frac{2a}{\frac{5}{13}}=\frac{26}{5}a\]

Pertanto:

\[Area(ABV)=\frac{AB\cdot VH}{2}=\frac{1}{2}(6a)\left(\frac{26}{5}a\right)=\frac{78}{5}a^2\]

La distanza h di C dalla faccia ABV, altezza della piramide rispetto alla base ABV è allora:

\[h=\frac{3V}{Area(ABV)}=\frac{3\cdot \frac{192}{5}a^3}{\frac{78}{5}a^2}=\frac{576}{78}a=\frac{96}{13}a\]

La distanza di C dal piano della faccia ABV è \(h=\frac{96}{13}a\).

Soluzione del punto 3

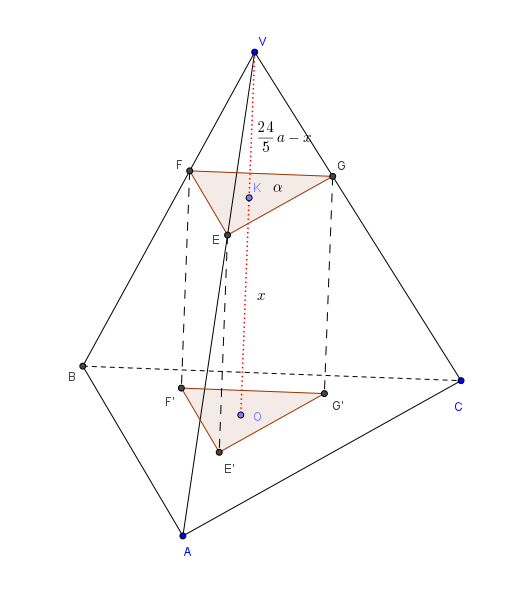
Indicata con \(x\) l’altezza del prisma (con \(0 < x < \frac{24}{5}a\)), la distanza VK del piano \(\alpha\) dal vertice V della piramide è data dalla differenza tra l’altezza VO della piramide e tale distanza \(x\), cioè: \(\frac{24}{5}a-x\).

Detto EFG il triangolo sezione tra il piano \(\alpha\) e la piramide, per una nota proprietà risulta:

\[Area(ABC):Area(EFG)=VO^2:VK^2\]

da cui:

\[Area(EFG)=Area(ABC)\cdot\frac{VK^2}{VO^2}=24a^2\cdot\frac{\left(\frac{24}{5}a-x\right)^2}{\left(\frac{24}{5}a\right)^2}\] \[Area(EFG)=\frac{25}{24}\cdot\left(\frac{24}{5}a-x\right)^2\]

il volume del prisma è dato da:

\[V(x)= Area(EFG)\cdot OK=\frac{25}{24}\cdot\left(\frac{24}{5}a-x\right)^2\cdot x\]

Tale volume è massimo se lo è l'espressione:

\[f(x)=\left(\frac{24}{5}a-x\right)^2\cdot x\] ---

Metodo 1: Proprietà delle potenze

Essendo il prodotto di due potenze con somma delle basi costante, esso risulta massimo se le basi sono proporzionali agli esponenti, quindi:

\[\frac{\frac{24}{5}a-x}{2}=\frac{x}{1} \implies \frac{24}{5}a-x=2x \implies 3x=\frac{24}{5}a \implies x=\frac{8}{5}a\] ---

Metodo 2: Uso delle derivate (studio della monotonia)

Sviluppiamo la funzione \(f(x)\):

\[f(x) = \left(\left(\frac{24}{5}a\right)^2 - 2\left(\frac{24}{5}a\right)x + x^2\right) \cdot x\] \[f(x) = \frac{576}{25}a^2x - \frac{48}{5}ax^2 + x^3\]

Calcoliamo la derivata prima \(f'(x)\):

\[f'(x) = \frac{d}{dx}\left(\frac{576}{25}a^2x - \frac{48}{5}ax^2 + x^3\right)\] \[f'(x) = \frac{576}{25}a^2 - \frac{96}{5}ax + 3x^2\]

Poniamo la derivata prima uguale a zero per trovare i punti critici:

\[3x^2 - \frac{96}{5}ax + \frac{576}{25}a^2 = 0\]

Moltiplichiamo per 25 per eliminare i denominatori:

\[75x^2 - 480ax + 576a^2 = 0\]

Risolviamo l'equazione quadratica per \(x\) usando la formula risolutiva:

\[x = \frac{-(-480a) \pm \sqrt{(-480a)^2 - 4 \cdot 75 \cdot 576a^2}}{2 \cdot 75}\] \[x = \frac{480a \pm \sqrt{230400a^2 - 172800a^2}}{150}\] \[x = \frac{480a \pm \sqrt{57600a^2}}{150}\] \[x = \frac{480a \pm 240a}{150}\]

Otteniamo due possibili soluzioni per \(x\):

\[x_1 = \frac{480a - 240a}{150} = \frac{240a}{150} = \frac{24a}{15} = \frac{8}{5}a\] \[x_2 = \frac{480a + 240a}{150} = \frac{720a}{150} = \frac{72a}{15} = \frac{24}{5}a\]

Ora, studiamo il **segno della derivata prima** \(f'(x) = 3x^2 - \frac{96}{5}ax + \frac{576}{25}a^2\). Poiché il coefficiente di \(x^2\) è positivo (\(3 > 0\)), la parabola che rappresenta \(f'(x)\) ha concavità verso l'alto. I valori di \(x\) che annullano \(f'(x)\) sono \(x_1 = \frac{8}{5}a\) e \(x_2 = \frac{24}{5}a\). Pertanto:

• Per \(x < \frac{8}{5}a\), \(f'(x) > 0\), quindi \(f(x)\) è **crescente**.
• Per \(\frac{8}{5}a < x < \frac{24}{5}a\), \(f'(x) < 0\), quindi \(f(x)\) è **decrescente**.
• Per \(x > \frac{24}{5}a\), \(f'(x) > 0\), quindi \(f(x)\) è **crescente**.

Considerando le limitazioni geometriche del problema, \(0 < x < \frac{24}{5}a\), la funzione \(f(x)\) (e quindi il volume \(V(x)\)) è:

• Crescente per \(0 < x < \frac{8}{5}a\)
• Decrescente per \(\frac{8}{5}a < x < \frac{24}{5}a\)

Questo significa che la funzione \(f(x)\) raggiunge il suo **massimo** quando \(x = \frac{8}{5}a\).

Da entrambi i metodi si deduce che il volume del prisma è massimo quando la sua altezza è \(\frac{8}{5}a\).

Soluzione del punto 4

La superficie totale del prisma è data da:

\[S=2A(base)+S_l=2A(EFG)+perimetro(EFG)\cdot OK\] \[Area(EFG)=\frac{25}{24}\cdot\left(\frac{24}{5}a-x\right)^2\]

dove \(x=OK\).

Il triangolo EFG è simile al triangolo ABC e il rapporto di similitudine è uguale al rapporto fra VK e VO.

\[k = \frac{VK}{VO} = \frac{\frac{24}{5}a-x}{\frac{24}{5}a} = \frac{24a-5x}{24a}\]

Il rapporto tra il perimetro di EFG e quello di ABC è uguale a \(k\); perciò:

\[2p(EFG)=k\cdot 2p(ABC)=\frac{24a-5x}{24a}\cdot 24a=24a-5x\]

Si ha allora:

\[S(x)=2A(EFG)+2p(EFG)\cdot OK=2\cdot\frac{25}{24}\cdot\left(\frac{24}{5}a-x\right)^2+(24a-5x)\cdot x\] \[S(x)=\frac{25}{12}\left(\frac{24}{5}a-x\right)^2+x(24a-5x)\]

Sviluppando e semplificando:

\[S(x)=\frac{25}{12}\left(\frac{576}{25}a^2 - \frac{48}{5}ax + x^2\right) + 24ax - 5x^2\] \[S(x)=24a^2 - 20ax + \frac{25}{12}x^2 + 24ax - 5x^2\] \[S(x)=48a^2 + 4ax - \frac{35}{12}x^2\]

Per trovare il massimo, calcoliamo la derivata prima \(S'(x)\):

\[S'(x)=4a-\frac{35}{6}x\]

Poniamo \(S'(x) \ge 0\) per studiare la crescenza della funzione:

\[4a-\frac{35}{6}x \ge 0 \implies 4a \ge \frac{35}{6}x \implies x \le \frac{24}{35}a\]

Considerando il dominio \(0 < x < \frac{24}{5}a\), si ha che \(S(x)\) è crescente per \(0 < x < \frac{24}{35}a\) e decrescente per \(\frac{24}{35}a < x < \frac{24}{5}a\). Pertanto,

L'area totale \(S\) è massima quando \(x=\frac{24}{35}a\), che è diverso dal valore \(x=\frac{8}{5}a\) per il quale è massimo il volume.

Concludiamo che il prisma di volume massimo **non ha anche la massima area totale**.