Problema 8 con tipologia Esame di Stato


Funzioni e derivate in Medicina
Risolvi da solo i vari punti del problema e controlla le soluzioni premendo il tasto corrispondente.
Il dottor Rossi lavora in una clinica veterinaria e si sta occupando di un cucciolo di gatto colpito da un’infezione batterica. Per contrastare la malattia è necessaria una dose di antibiotico da somministrare per via intramuscolare. A partire dall’istante x=0 in cui viene eseguita l’iniezione, la concentrazione del farmaco nel sangue dell’animale, espressa in mg/L, è modellizzata da una funzione del tipo: \(f(x) = ax e^{-bx}\), dove \(a\) e \(b\) sono parametri reali positivi e \(x \ge 0\) indica il tempo trascorso dalla somministrazione iniziale espresso in ore.
1)
Determina per quali valori dei parametri \(a\) e \(b\) il valore massimo della concentrazione del farmaco, pari a 2 mg/L, si raggiunge dopo 1 ora.
Soluzione del punto 1
Per determinare i valori dei parametri \(a\) e \(b\) per cui la concentrazione del farmaco raggiunge un massimo di 2 mg/L dopo 1 ora, dobbiamo analizzare la funzione \(f(x) = ax e^{-bx}\).
Derivata della funzione
Per determinare i valori dei parametri \(a\) e \(b\) per cui la concentrazione del farmaco raggiunge un massimo di 2 mg/L dopo 1 ora, dobbiamo analizzare la funzione \(f(x) = ax e^{-bx}\).
Derivata della funzione
Per trovare il valore massimo della funzione, dobbiamo calcolare la derivata prima e porla uguale a zero.
\[f'(x) = \frac{d}{dx}(ax e^{-bx})\]Applichiamo la regola del prodotto \((uv)' = u'v + uv'\) dove \(u = ax\) e \(v = e^{-bx}\).
\[u' = a\] \[v' = -be^{-bx}\]Quindi,
\[f'(x) = a \cdot e^{-bx} + ax \cdot (-be^{-bx})\] \[f'(x) = ae^{-bx} - abxe^{-bx}\]Raccogliamo il termine comune \(ae^{-bx}\):
\[f'(x) = ae^{-bx}(1 - bx)\]Ricerca del punto di massimo e studio del segno della derivata prima
Ora, poniamo \(f'(x) = 0\) per trovare i punti critici.
\[ae^{-bx}(1 - bx) = 0\]Poiché \(a > 0\) e \(e^{-bx} > 0\) per ogni \(x\), l'espressione è zero solo se:
\[1 - bx = 0\] \[bx = 1\] \[x = \frac{1}{b}\]Per studiare il segno della derivata prima, consideriamo \(f'(x) = ae^{-bx}(1 - bx)\). Dato che \(a > 0\) e \(e^{-bx} > 0\) per ogni \(x\), il segno di \(f'(x)\) dipende interamente dal segno di \((1 - bx)\):
- Se \(1 - bx > 0 \implies bx < 1 \implies x < \frac{1}{b}\), allora \(f'(x) > 0\), e la funzione \(f(x)\) è **crescente**.
- Se \(1 - bx < 0 \implies bx > 1 \implies x > \frac{1}{b}\), allora \(f'(x) < 0\), e la funzione \(f(x)\) è **decrescente**.
Questo cambio di segno da positivo a negativo intorno a \(x = \frac{1}{b}\) conferma che in \(x = \frac{1}{b}\) la funzione \(f(x)\) presenta un **massimo relativo**.
Applicazione delle condizioni date
Il problema ci dice che il valore massimo della concentrazione si raggiunge dopo **1 ora**, quindi:
\[x_{max} = 1\] \[\frac{1}{b} = 1 \implies \mathbf{b = 1}\]Ora, dobbiamo usare l'altra condizione: il valore massimo della concentrazione è **2 mg/L**. Sostituiamo \(x = 1\) e \(b = 1\) nella funzione originale \(f(x)\):
\[f(x_{max}) = a(1)e^{-b(1)}\] \[2 = a \cdot e^{-1}\] \[2 = \frac{a}{e}\] \[\mathbf{a = 2e}\]Conclusione
Quindi, i valori dei parametri sono:
- \(a = 2e\)
- \(b = 1\)
Con questi valori, la funzione della concentrazione del farmaco diventa \(f(x) = 2ex e^{-x}\).
2)
Il dottor Rossi dichiara che, in corrispondenza dei valori trovati nel punto precedente, l’espressione analitica della funzione è \(f(x) = 2xe^{(1-x)}\). Dopo aver verificato l’affermazione, rappresenta il grafico della funzione \(f(x)\) per \(x \ge 0\) determinando le coordinate del flesso \(F\), verificando che ha ascissa uguale a 2, e l’equazione della tangente nel punto F.
Soluzione del punto 2
Verifica dell'espressione analitica
Nel punto precedente abbiamo determinato che \(a = 2e\) e \(b = 1\). Sostituendo questi valori nella funzione generale \(f(x) = ax e^{-bx}\), otteniamo:
\[f(x) = (2e)x e^{-(1)x}\] \[f(x) = 2ex e^{-x}\]Quindi, possiamo riscrivere l'espressione come:
\[f(x) = 2x(e \cdot e^{-x})\] \[f(x) = 2x e^{1-x}\]Questo verifica l'affermazione del dottor Rossi.
Studio di funzione e grafico
Per rappresentare il grafico della funzione \(f(x) = 2x e^{1-x}\) per \(x \ge 0\), analizziamo i suoi comportamenti principali.
Dominio
Il dominio è \(x \ge 0\).
Intersezioni con gli assi
- Asse y: Per \(x=0\), \(f(0) = 2(0)e^{1-0} = 0\). La funzione passa per l'origine \((0,0)\).
- Asse x: Per \(f(x)=0\), \(2xe^{1-x} = 0\). Poiché \(e^{1-x}\) è sempre positivo, \(2x = 0 \implies x=0\). L'unica intersezione è l'origine.
Comportamento agli estremi
- Per \(x \to 0^+\), \(f(x) \to 0\).
- Per \(x \to +\infty\), \(f(x) = 2x e^{1-x} = \frac{2x}{e^{x-1}}\). L'esponenziale cresce più velocemente di qualsiasi potenza di \(x\), quindi \(f(x) \to 0\). L'asse x è un asintoto orizzontale per \(x \to +\infty\).
Derivata prima e massimi/minimi
Dalla soluzione del punto 1, sappiamo che \(f'(x) = ae^{-bx}(1 - bx)\). Sostituendo \(a=2e\) e \(b=1\):
\[f'(x) = 2e \cdot e^{-x}(1 - 1x)\] \[f'(x) = 2e^{1-x}(1 - x)\]Ponendo \(f'(x) = 0\), abbiamo \(1 - x = 0 \implies x = 1\).
Studiamo il segno di \(f'(x)\):
- Per \(0 \le x < 1\), \(1-x > 0\), quindi \(f'(x) > 0\). La funzione è **crescente**.
- Per \(x > 1\), \(1-x < 0\), quindi \(f'(x) < 0\). La funzione è **decrescente**.
In \(x=1\), la funzione ha un **massimo relativo** (che è anche assoluto dato il comportamento agli estremi). Il valore massimo è \(f(1) = 2(1)e^{1-1} = 2e^0 = 2\). Quindi, il punto di massimo è \((1, 2)\).
Determinazione del flesso F
Per trovare i punti di flesso, dobbiamo calcolare la derivata seconda e porla uguale a zero.
\[f''(x) = \frac{d}{dx}(2e^{1-x}(1 - x))\]Applichiamo la regola del prodotto con \(u = 2e^{1-x}\) e \(v = (1 - x)\).
\[u' = 2e^{1-x} \cdot (-1) = -2e^{1-x}\] \[v' = -1\]Quindi,
\[f''(x) = (-2e^{1-x})(1 - x) + (2e^{1-x})(-1)\] \[f''(x) = -2e^{1-x} + 2xe^{1-x} - 2e^{1-x}\] \[f''(x) = 2xe^{1-x} - 4e^{1-x}\]Raccogliamo il termine comune \(2e^{1-x}\):
\[f''(x) = 2e^{1-x}(x - 2)\]Poniamo \(f''(x) = 0\):
\[2e^{1-x}(x - 2) = 0\]Poiché \(2e^{1-x}\) è sempre positivo, l'espressione è zero solo se:
\[x - 2 = 0 \implies x = 2\]Verifichiamo che l'ascissa del flesso è uguale a 2, come richiesto dal problema.
Studiamo il segno di \(f''(x)\):
- Per \(0 \le x < 2\), \(x - 2 < 0\), quindi \(f''(x) < 0\). La funzione è **concava verso il basso**.
- Per \(x > 2\), \(x - 2 > 0\), quindi \(f''(x) > 0\). La funzione è **concava verso l'alto**.
Il cambio di concavità in \(x=2\) conferma che \(x=2\) è l'ascissa di un punto di flesso.
Calcoliamo l'ordinata del flesso \(F\):
\[f(2) = 2(2)e^{1-2} = 4e^{-1} = \frac{4}{e}\]Le coordinate del flesso \(F\) sono \(\left(2, \frac{4}{e}\right)\).
Equazione della tangente nel punto F
Per trovare l'equazione della retta tangente nel punto \(F(2, \frac{4}{e})\), usiamo la formula \(y - y_0 = m(x - x_0)\), dove \(m = f'(x_0)\) è il coefficiente angolare della tangente.
Calcoliamo \(f'(2)\):
\[f'(2) = 2e^{1-2}(1 - 2)\] \[f'(2) = 2e^{-1}(-1)\] \[f'(2) = -\frac{2}{e}\]Ora, sostituiamo \(x_0=2\), \(y_0=\frac{4}{e}\) e \(m=-\frac{2}{e}\) nell'equazione della retta:
\[y - \frac{4}{e} = -\frac{2}{e}(x - 2)\] \[y - \frac{4}{e} = -\frac{2}{e}x + \frac{4}{e}\] \[y = -\frac{2}{e}x + \frac{4}{e} + \frac{4}{e}\] \[\mathbf{y = -\frac{2}{e}x + \frac{8}{e}}\]L'equazione della tangente nel punto di flesso \(F\) è \(y = -\frac{2}{e}x + \frac{8}{e}\).
Grafico della funzione
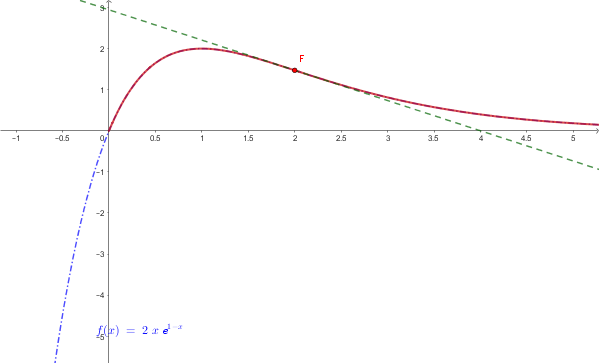
3)
In quale intervallo di tempo la velocità di variazione della concentrazione del farmaco nel sangue del cucciolo è positiva? Qual è il valore della velocità di variazione della concentrazione del farmaco dopo 2 ore?
Soluzione del punto 3
Intervallo in cui la velocità di variazione è positiva
La velocità di variazione della concentrazione del farmaco è data dalla derivata prima della funzione \(f(x)\). Nel punto 1, abbiamo trovato la funzione \(f(x) = 2x e^{1-x}\) e la sua derivata prima:
\[f'(x) = 2e^{1-x}(1 - x)\]Per determinare l'intervallo in cui la velocità di variazione è positiva, dobbiamo studiare il segno di \(f'(x)\).
Abbiamo già stabilito che \(2e^{1-x}\) è sempre positivo per ogni \(x\). Pertanto, il segno di \(f'(x)\) dipende unicamente dal segno del fattore \((1 - x)\):
- Se \(1 - x > 0 \implies x < 1\), allora \(f'(x) > 0\).
- Se \(1 - x < 0 \implies x > 1\), allora \(f'(x) < 0\).
- Se \(1 - x = 0 \implies x = 1\), allora \(f'(x) = 0\).
Considerando il dominio fisico del problema, \(x \ge 0\), la velocità di variazione della concentrazione del farmaco è **positiva** nell'intervallo di tempo:
\[\mathbf{0 \le x < 1 \text{ ore}}\]Questo significa che la concentrazione del farmaco nel sangue del cucciolo aumenta dal momento della somministrazione fino a 1 ora dopo.
Valore della velocità di variazione dopo 2 ore
Per calcolare il valore della velocità di variazione della concentrazione del farmaco dopo 2 ore, dobbiamo semplicemente sostituire \(x = 2\) nella derivata prima \(f'(x)\):
\[f'(x) = 2e^{1-x}(1 - x)\] \[f'(2) = 2e^{1-2}(1 - 2)\] \[f'(2) = 2e^{-1}(-1)\] \[f'(2) = -\frac{2}{e}\]Il valore di \(\frac{2}{e}\) è circa \(\frac{2}{2.718} \approx 0.736\). Quindi, \(f'(2) \approx -0.736\).
La velocità di variazione della concentrazione del farmaco dopo 2 ore è \(\mathbf{-\frac{2}{e} \text{ mg/L per ora}}\). Il segno negativo indica che la concentrazione del farmaco sta diminuendo in quel momento.
4)
Il dottor Rossi osserva che la funzione \(f(x)\) è un ottimo modello per la concentrazione del farmaco nel sangue solo nelle prime 2 ore dalla somministrazione. Da questo momento in poi la concentrazione decresce linearmente, seguendo l’andamento della tangente nel punto F.
Dopo quanto tempo dall’iniezione il cucciolo avrà completamente smaltito l’antibiotico somministrato? Scrivi l’espressione analitica del nuovo modello dall’istante iniziale \(x = 0\), fino all’istante in cui non ci sarà più traccia del farmaco nel sangue dell’animale e rappresenta il grafico della funzione trovata.
Soluzione del punto 4
Nuovo modello della funzione
Il problema ci dice che la funzione \(f(x) = 2x e^{1-x}\) è un ottimo modello per la concentrazione del farmaco solo per \(0 \le x \le 2\) ore. Da \(x = 2\) ore in poi, la concentrazione decresce linearmente seguendo l'andamento della tangente nel punto di flesso \(F\).
Abbiamo già calcolato nel punto 2:
- Le coordinate del flesso \(F\): \(\left(2, \frac{4}{e}\right)\).
- L'equazione della tangente nel punto \(F\): \(y = -\frac{2}{e}x + \frac{8}{e}\).
Il nuovo modello di concentrazione, che chiamiamo \(C(x)\), sarà una funzione definita a tratti:
\[ C(x) = \begin{cases} 2x e^{1-x} & \text{per } 0 \le x \le 2 \\ -\frac{2}{e}x + \frac{8}{e} & \text{per } x > 2 \end{cases} \]Grafico del nuovo modello della funzione
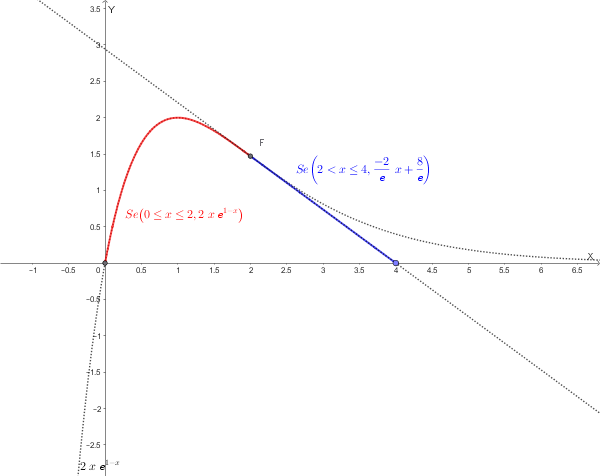
Tempo di smaltimento completo dell'antibiotico
Il cucciolo avrà completamente smaltito l'antibiotico quando la concentrazione del farmaco nel sangue sarà zero. Questo avviene quando la parte lineare del modello interseca l'asse delle ascisse (\(C(x) = 0\)).
Poniamo la parte lineare uguale a zero:
\[-\frac{2}{e}x + \frac{8}{e} = 0\]Moltiplichiamo entrambi i lati per \(e\) per eliminare il denominatore:
\[-2x + 8 = 0\] \[2x = 8\] \[x = 4\]Questo significa che la concentrazione del farmaco raggiunge lo zero dopo **4 ore** dall'iniezione.
Rappresentazione grafica della funzione trovata
Il grafico della funzione \(C(x)\) sarà composto da due parti:
- **Per \(0 \le x \le 2\):** La curva della funzione esponenziale \(f(x) = 2x e^{1-x}\).
- Inizia dall'origine \((0,0)\).
- Raggiunge un massimo in \((1, 2)\).
- Ha un flesso in \(\left(2, \frac{4}{e}\right)\), dove \(\frac{4}{e} \approx \frac{4}{2.718} \approx 1.47\).
- **Per \(2 < x \le 4\):** Un segmento di retta che è la tangente nel punto di flesso \(F\).
- Parte dal punto \(F\left(2, \frac{4}{e}\right)\).
- Termina nel punto \((4, 0)\) sull'asse delle ascisse, dove la concentrazione si azzera.
Il grafico mostra una curva che cresce da 0 a 1, poi decresce fino a \(x=2\), mantenendo una concavità verso il basso fino a \(x=2\) e diventando una retta discendente da \(x=2\) fino a \(x=4\) dove tocca lo zero.