Risolvi da solo i vari punti del problema e controlla le soluzioni premendo il tasto corrispondente.
Un'azienda produce un bene la cui funzione di **costo totale di produzione** è data da \(C(x) = ax^3 + bx^2 + cx + d\), dove \(x \ge 0\) è la quantità di bene prodotta (in migliaia di unità) e \(C(x)\) è il costo totale in migliaia di euro. Si definisce **Costo marginale** la variazione del costo totale di produzione che si verifica quando si produce una unità aggiuntiva di un bene. Il Costo marginale misura l'incremento di costo generato da un aumento infinitesimo della quantità prodotta ed è quindi pari alla **derivata prima** \(C'(x)\) della funzione Costo totale \(C(x)\) rispetto alla quantità prodotta \(x\): \(C'(x) = \frac{dC(x)}{dx}\). Sappiamo che il costo fisso iniziale (per \(x=0\)) è di 10 migliaia di euro. Inoltre, il costo marginale ha un valore minimo di 1 migliaio di euro per unità in corrispondenza di una produzione di 1000 unità (\(x=1\)), e il costo marginale è di 10 migliaia di euro per unità quando la produzione è di 2000 unità (\(x=2\)).
1)
Determina i valori dei parametri \(a\), \(b\), \(c\), e \(d\) e scrivi l'espressione analitica della funzione di costo totale \(C(x)\) e della funzione di costo marginale \(C'(x)\). **Successivamente, studia la funzione \(C(x)\) e rappresentala graficamente per \(x \ge 0\).**
Soluzione del punto 1
Determinazione dei parametri
La funzione di costo totale è \(C(x) = ax^3 + bx^2 + cx + d\). La funzione di costo marginale è la sua derivata prima:
\[C'(x) = 3ax^2 + 2bx + c\]Applicando le quattro condizioni date, si ottiene il sistema di equazioni che porta ai parametri:
\[\begin{cases} C(0) = 10 \implies d = 10 \\ C'(1) = 1 \implies 3a + 2b + c = 1 \\ C''(1) = 0 \implies 6a + 2b = 0 \implies b = -3a \\ C'(2) = 10 \implies 12a + 4b + c = 10 \end{cases}\]Risolvendo il sistema, si trovano i valori:
\[\mathbf{a = 3}, \quad \mathbf{b = -9}, \quad \mathbf{c = 10}, \quad \mathbf{d = 10}\]Le espressioni analitiche delle funzioni sono:
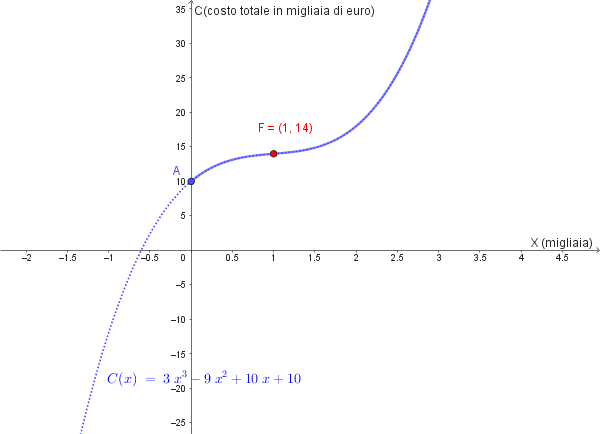
- **Funzione di costo totale:** \[\mathbf{C(x) = 3x^3 - 9x^2 + 10x + 10}\]
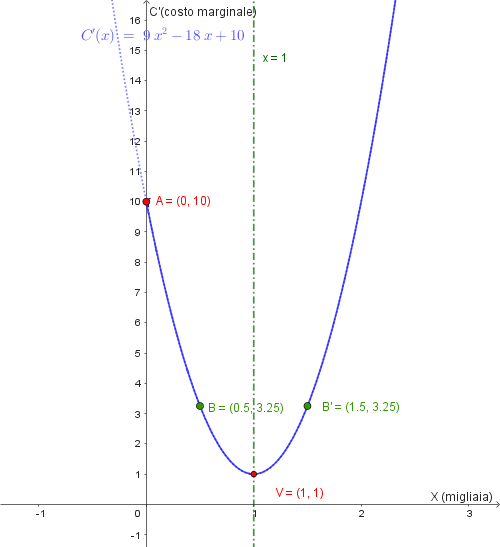
- **Funzione di costo marginale:** \[\mathbf{C'(x) = 9x^2 - 18x + 10}\]
Studio e Grafico della funzione di costo totale \(C(x)\)
La funzione da studiare è \(C(x) = 3x^3 - 9x^2 + 10x + 10\) con dominio \(x \ge 0\).
Intersezione con gli assi e limiti
- **Asse y (\(x=0\))**: \(C(0) = 10\). Il punto di partenza (costo fisso) è \((0, 10)\).
- **Asse x (\(C(x)=0\))**: \(C(x) > 0\) per \(x \ge 0\), quindi non ci sono intersezioni con l'asse x.
- **Limite**: \(\lim_{x \to +\infty} C(x) = +\infty\).
Derivata Prima (Monotonia)
La derivata prima è la funzione di Costo Marginale:
\[C'(x) = 9x^2 - 18x + 10\]Per trovare massimi e minimi, poniamo \(C'(x) = 0\):
\[9x^2 - 18x + 10 = 0\]Discriminante:
\[\Delta = (-18)^2 - 4(9)(10) = 324 - 360 = -36\]Poiché \(\Delta < 0\) e il coefficiente dominante è positivo, si ha che \(\mathbf{C'(x) > 0}\) per ogni \(x\). La funzione \(C(x)\) è quindi sempre crescente per \(x \ge 0\).
Derivata Seconda (Concavità e Flessi)
La derivata seconda è:
\[C''(x) = 18x - 18\]Punto di flesso:
\[18x - 18 = 0 \implies x = 1\]Ordinata del flesso:
\[C(1) = 14 \implies F(1,14)\]- Per \(x < 1\), \(C''(x) < 0\) → concavità verso il basso
- Per \(x > 1\), \(C''(x) > 0\) → concavità verso l'alto
Grafico della funzione C(x):
2)
Verifica che la funzione di costo marginale \(C'(x)\) ha come asse di simmetria la retta \(x=1\). **Dai un'interpretazione economica di questa simmetria** e rappresenta il grafico di \(C'(x)\) per \(x \ge 0\).
Soluzione del punto 2
Verifica e Interpretazione dell'asse di simmetria
La funzione di costo marginale è una parabola: \(\mathbf{C'(x) = 9x^2 - 18x + 10}\).
Una parabola con equazione \(y = Ax^2 + Bx + C\) ha come asse di simmetria la retta passante per il vertice e parallela all'asse delle ordinate. L'ascisa del vertice è data da:
\[x_v = -\frac{B}{2A}\]Nel nostro caso, \(A=9\) e \(B=-18\). Sostituendo i valori:
\[x_v = -\frac{-18}{2(9)} = \frac{18}{18} = 1\]Quindi la parabola ha per asse di simmetria la retta \(\mathbf{x=1}\).
Interpretazione Economica della Simmetria
L'asse di simmetria della funzione di Costo Marginale \(C'(x)\) si trova in \(\mathbf{x=1}\). Poiché la parabola ha la concavità rivolta verso l'alto, questo punto (\(x=1\)) corrisponde al **minimo assoluto** del costo marginale (il **vertice** della parabola), che è \(C'(1)=1\).
La simmetria attorno a \(x=1\) significa che, per ogni quantità di produzione \(\Delta x\) in più o in meno rispetto al livello \(x=1\) (che minimizza il costo aggiuntivo), l'**incremento del costo marginale è lo stesso**.
- Ad esempio, il costo marginale per produrre 0.5 migliaia di unità (\(x=1-0.5=0.5\)) è \[C'(0.5) = 9(0.5)^2 - 18(0.5) + 10 = 9(0.25) - 9 + 10 = 2.25 + 1 = 3.25\]
- Il costo marginale per produrre 1.5 migliaia di unità (\(x=1+0.5=1.5\)) è anch'esso \[C'(1.5) = 9(1.5)^2 - 18(1.5) + 10 = 9(2.25) - 27 + 10 = 20.25 - 17 = 3.25\]
Questa simmetria evidenzia che la deviazione da **1000 unità** (il punto di produzione più efficiente, dove \(C'(x)\) è minimo) causa lo stesso aumento di costo marginale (3,25 migliaia di euro per unità), sia che si produca un po' meno (\(x=0.5\)), sia che si produca un po' di più (\(x=1.5\)).
Grafico della funzione di costo marginale \(C'(x)\)
Per rappresentare il grafico, individuiamo i punti chiave per \(x \ge 0\):
- **Vertice (minimo):** L'ascissa è \(x_v = 1\). L'ordinata è: \[C'(1) = 9(1)^2 - 18(1) + 10 = 1\] Il vertice è \(\mathbf{V(1, 1)}\).
- **Intersezione con l'asse y (\(x=0\)):** \[C'(0) = 9(0)^2 - 18(0) + 10 = 10\] Il punto è \(\mathbf{(0, 10)}\). Questo è il costo marginale per una produzione quasi nulla.
- **Punto per \(x=2\):** Sfruttando la simmetria rispetto a \(x=1\): \[C'(2) = 9(2)^2 - 18(2) + 10 = 10\] Il punto è \(\mathbf{(2, 10)}\).
La parabola ha la concavità rivolta verso l'alto (\(A=9 > 0\)). Il grafico è una curva che parte da \((0, 10)\), scende fino al minimo \((1, 1)\) e risale.
Il grafico della funzione \(C'(x)\) è questo:
3)
Calcola il **costo medio** (o costo unitario) di produzione, \(C_m(x)\) e determina per quale quantità \(x\) il costo medio è minimo. Qual è il valore di questo costo medio minimo?
Soluzione del punto 3
Funzione di costo medio \(C_m(x)\)
Il costo medio è definito come il costo totale diviso per la quantità prodotta (\(x\)):
\[C_m(x) = \frac{C(x)}{x} = \frac{3x^3 - 9x^2 + 10x + 10}{x}\] \[\mathbf{C_m(x) = 3x^2 - 9x + 10 + \frac{10}{x}}\]Ricerca del Costo Medio Minimo
Per trovare il minimo di \(C_m(x)\), calcoliamo la sua derivata prima, \(C_m'(x)\), e la poniamo a zero. Calcoliamo la derivsat.
\[C_m'(x) = \frac{d}{dx} \left(3x^2 - 9x + 10 + 10x^{-1}\right)\] \[C_m'(x) = 6x - 9 - 10x^{-2}\] \[C_m'(x) = 6x - 9 - \frac{10}{x^2}\]Studio del segno della derivata prima di \(C_m(x)\):
\[6x - 9 - \frac{10}{x^2} ≥ 0\] \[\text{Moltiplichiamo per } x^2: \quad 6x^3 - 9x^2 - 10 ≥ 0\]
Per studiare questa disequazione, facciamo uno studio qualitativo della funzione:
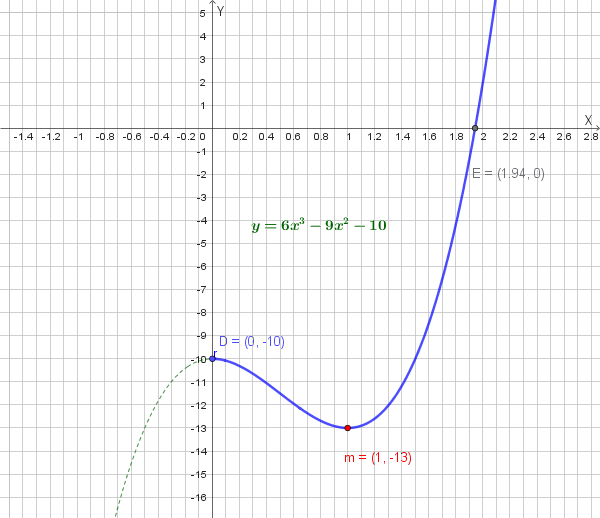
consideriamo la cubica \(y = 6x^3 - 9x^2 - 10\)
Studio qualitativo della funzione
1. Intersezione con l'asse y:
\(y(0) = 6 \cdot 0^3 - 9 \cdot 0^2 - 10 = -10\)
La cubica passa per il punto (0, -10)
2. Limiti agli estremi:
\(\lim_{x \to +\infty} y(x) = +\infty\),
\(\lim_{x \to -\infty} y(x) = -\infty\)
3. Derivata prima e monotonia:
\(y'(x) = 18x^2 - 18x = 18x(x-1)\)
Segno della derivata:
- \(x<0 \Rightarrow y'>0\) → funzione crescente
- \( 0 < x < 1\Rightarrow y'<0 \) → funzione decrescente
- \(x>1 \Rightarrow y'>0\) → funzione crescente
4. Massimi e minimi locali:
Punti critici: \(x=0\) e \(x=1\)
Valori delle ordinate:
- \(y(0) = -10\) → massimo locale
- \(y(1) = 6 - 9 - 10 = -13\) → minimo locale
Lo studio fatto ci permette di dire che il grafico della cubica taglia l'asse delle x in un solo punto di ascissa \(x_0\) che vale poco meno di 2.
Quindi:
\[ 6x^3 - 9x^2 - 10 \ge 0 \quad \text{se } \ x\ge x_0 \]
La funzione è quindi positiva per \(x > x_0\) e negativa per \(0 \le x < x_0\).
Il grafico della cubica è di questo tipo:
Tabulazione per valore approssimato della radice
Calcoliamo alcuni valori per trovare \(x_0\) approssimativamente:
| x | \(y(x) = 6x^3 - 9x^2 - 10\) |
|---|---|
| 1.8 | \(y(1.8) = 6(1.8)^3 - 9(1.8)^2 - 10 ≈ -3.4 \) |
| 1.9 | \(y(1.9) = 6(1.9)^3 - 9(1.9)^2 - 10 ≈ -1.3\) |
| 1.94 | \(y(1.94) ≈ -0.07\) |
| 1.95 | \(y(1.95) ≈ 0.20\) |
| 2.0 | \(y(2.0) = 6(2)^3 - 9(2)^2 - 10 = 2\) |
Dalla tabulazione si vede chiaramente che \(y(x)\) cambia segno tra 1.94 e 1.95 → la radice \(x_0 \approx 1.94\).
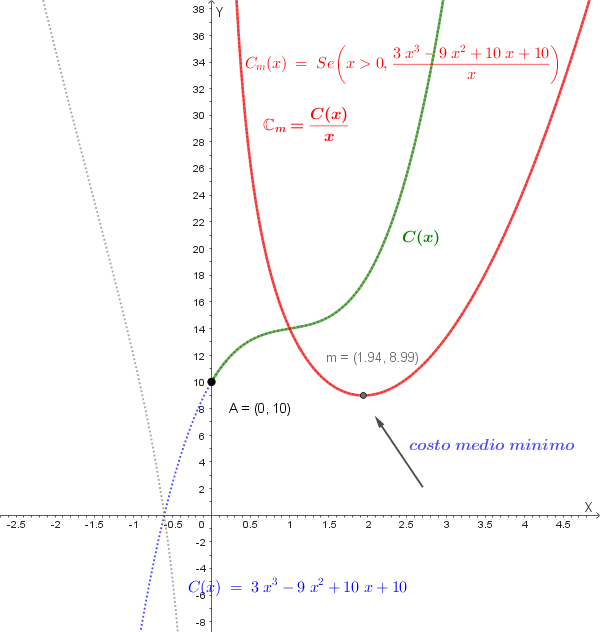
In termini di quantità prodotta, il costo medio è minimo per circa **1940 unità**.
Valore del costo medio minimo
Per calcolare il valore del costo medio minimo in x ≈ 1.94, sostituiamo il valore approssimato nella funzione \(C_m(x)\):
\[C_m(1.94) \approx 3(1.94)^2 - 9(1.94) + 10 + \frac{10}{1.94}\] \[C_m(1.94) \approx 11.29 - 17.46 + 10 + 5.16 \approx 8.99 \]Il costo medio minimo è di circa 9 euro per unità.
Questo significa che, producendo circa 1.94 migliaia di unità (cioè circa 1 940 unità), l’azienda ottiene il livello più basso possibile di costo medio: ogni unità del bene costa in media circa 9 euro. Oltre questo livello di produzione i costi medi tornano ad aumentare, mentre al di sotto di esso l’impresa non sfrutta ancora pienamente le economie di scala. In altre parole, quando l’azienda produce poche unità, i costi fissi (come macchinari, energia, personale: costi che non cambiano al variare della produzione) vengono divisi tra poche unità prodotte, e quindi il costo per unità rimane alto. Aumentando la produzione, gli stessi costi fissi vengono distribuiti su più unità, e quindi il costo medio per unità diminuisce.
Grafico del costo totale e del costo medio. E' evidenziato il Costo Medio Minimo:
4)
Il profitto totale, \(P(x)\), è la differenza tra il ricavo totale e il costo totale: \(P(x) = R(x) - C(x)\). Assumiamo che il prezzo di vendita sia costante e pari a 15 migliaia di euro per unità, quindi il ricavo totale è \(R(x) = 15x\). Determina la quantità di produzione \(x\) che massimizza il profitto totale e il profitto massimo.
Soluzione del punto 4
Funzione di profitto totale \(P(x)\)
Il ricavo totale è \(R(x) = 15x\). Il costo totale è \(C(x) = 3x^3 - 9x^2 + 10x + 10\). La funzione di profitto si ottiene come differenza:
\[ P(x) = R(x) - C(x) \]
\[ P(x) = 15x - (3x^3 - 9x^2 + 10x + 10) \]
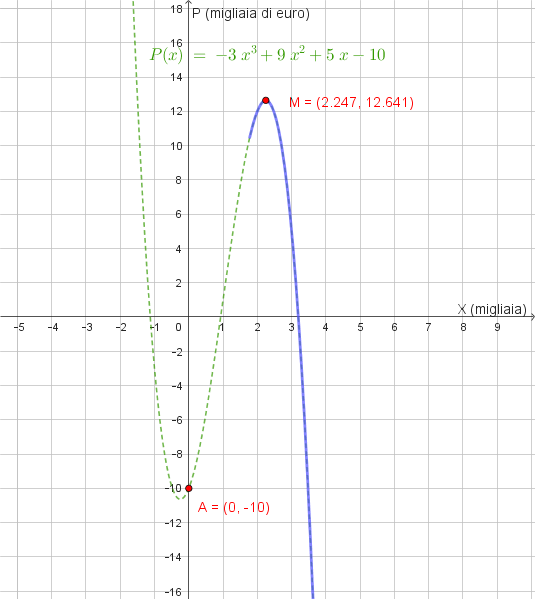
\[ P(x) = -3x^3 + 9x^2 + 5x - 10 \]
Ricerca della quantità che massimizza il profitto
Calcoliamo la derivata prima di \(P(x)\) per trovare i punti critici:
\[ P'(x) = \frac{d}{dx}(-3x^3 + 9x^2 + 5x - 10) \]
\[ P'(x) = -9x^2 + 18x + 5 \]
Poniamo \(P'(x) = 0\):
\[ -9x^2 + 18x + 5 = 0 \]
Moltiplichiamo per -1 per semplificare:
\[ 9x^2 - 18x - 5 = 0 \]
Risolviamo con la formula del secondo grado:
\[ x = \frac{18 \pm \sqrt{(-18)^2 - 4 \cdot 9 \cdot (-5)}}{2 \cdot 9} \]
\[ x = \frac{18 \pm \sqrt{324 + 180}}{18} \]
\[ x = \frac{18 \pm \sqrt{504}}{18} = \frac{18 \pm 6\sqrt{14}}{18} = \frac{3 \pm \sqrt{14}}{3} \]
Le due soluzioni sono:
- \(x_1 = \frac{3 - \sqrt{14}}{3} \approx -0.247\) (scartiamo perché \(x \ge 0\))
- \(x_2 = \frac{3 + \sqrt{14}}{3} \approx 2.247\)
Quindi il profitto è massimo per:
\[ x \approx 2.247 \]
In termini di unità, ciò corrisponde a circa 2247 unità.
Valore del profitto massimo
Sostituendo \(x \approx 2.247\) nella funzione di profitto:
\[ P(2.247) = -3(2.247)^3 + 9(2.247)^2 + 5(2.247) - 10 \]
Calcolando numericamente:
\[ P(2.247) \approx 12.641 \text{ migliaia di euro} \]
Il profitto massimo è quindi di circa 12 641 euro e si ottiene con la produzione di circa 2 247 unità del bene prodotto.
Grafico del Profitto. E' evidenziato il Profitto Massimo: