

Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.


Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.
Sia \( f(x) \) una funzione reale di variabile reale, continua nel campo reale, tale che \( f(0)=2 \). Calcolare: \[ \lim_{x \to 0} \frac{\int_0^x e^t f(t)\, dt}{e^x - 1} \] dove \( e \) è la base dei logaritmi naturali.
Soluzione quesito 1:
Per \(x \to 0\), il numeratore \(\int_0^x e^t f(t)\,dt \to 0\) e il denominatore \(e^x - 1 \to 0\): il limite si presenta nella forma indeterminata \(\frac{0}{0}\). Sono verificate le condizioni per applicare la regola di de L'Hôpital.
Deriviamo numeratore e denominatore. Per il Teorema di Torricelli, la derivata della funzione integrale è la funzione integranda:
\[ \frac{d}{dx}\int_0^x e^t f(t)\,dt = e^x f(x) \]Quindi:
\[ \lim_{x \to 0} \frac{\int_0^x e^t f(t)\,dt}{e^x - 1} = \lim_{x \to 0} \frac{e^x f(x)}{e^x} = \lim_{x \to 0} f(x) \]Per la continuità di \(f\) in \(x=0\):
\[ \lim_{x \to 0} f(x) = f(0) = 2 \]Il valore del limite è 2.
Si consideri il cubo di spigoli AA', BB', CC', DD', in cui due facce opposte sono i quadrati ABCD e A'B'C'D'. Sia E il punto medio dello spigolo AB. I piani ACC'A' e D'DE dividono il cubo in quattro parti. Dimostrare che la parte più estesa è il quintuplo di quella meno estesa.
Soluzione quesito 2:
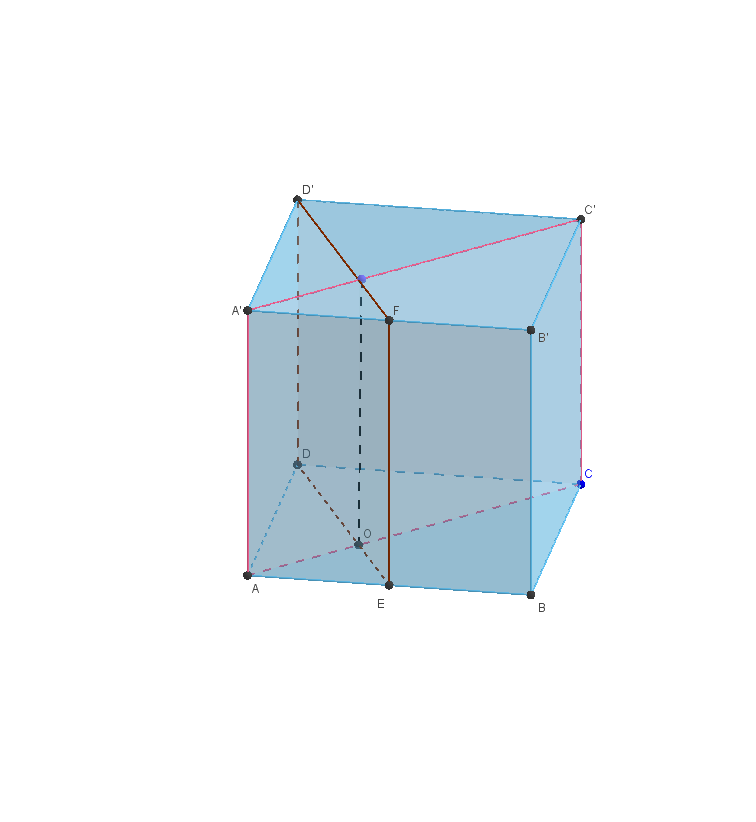
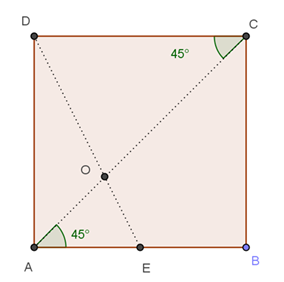
Le quattro parti sono prismi di altezza uguale \( AA' \) e basi le quattro parti in cui il quadrato \( ABCD \) resta diviso da \( DE \) ed \( AC \). Poniamo per comodità lo spigolo del cubo uguale a 2; risulta:
\[ AE = 1, \quad DE = \sqrt{5} \]Il triangolo \( AEO \) è simile al triangolo \( DOC \) ed essendo \( AE = \frac{1}{2} CD \), risulta:
\[ AO = \frac{1}{2} OC \]Essendo \( AC = 2\sqrt{2} \):
\[ AO = \frac{1}{3} AC = \frac{2\sqrt{2}}{3}, \qquad OC = 2AO = \frac{4\sqrt{2}}{3} \]Poiché il volume di un prisma è \( V = \text{Area(base)} \cdot h \) e i quattro prismi hanno la stessa altezza, il rapporto fra i volumi è uguale al rapporto fra le aree di base:
\[ \text{Area}(CBEO) = \frac{5}{3} = 5 \cdot \frac{1}{3} = 5 \cdot \text{Area}(AOE) \]Il prisma più esteso (base CBEO) ha volume quintuplo rispetto al prisma meno esteso (base AOE).
Considerata la funzione: \[ f(x) = ax^3 + 2ax^2 - 3x \] dove \( a \) è un parametro reale non nullo, determinare i valori di \( a \) per cui essa ha un massimo e un minimo relativi e quelli per cui non ha punti estremanti.
Soluzione quesito 3:
Poiché \( f \) è continua e derivabile su tutto \( \mathbb{R} \), per avere estremanti relativi è necessario che si annulli la derivata prima:
\[ f'(x) = 3ax^2 + 4ax - 3 = 0 \]Se \( \frac{\Delta}{4} > 0 \), la derivata ha due radici reali e distinte, quindi \(f\) ha un massimo e un minimo relativi:
\[ \frac{\Delta}{4} = 4a^2 + 9a > 0 \]Questa disequazione è verificata per:
\[ a < -\frac{9}{4} \quad \text{oppure} \quad a > 0 \]Se \( \frac{\Delta}{4} \leq 0 \), la derivata non cambia segno e \(f\) non ha estremanti:
\[ -\frac{9}{4} \leq a < 0 \]Determinare il numero delle soluzioni dell'equazione: \[ x e^x + x e^{-x} - 2 = 0 \]
Soluzione quesito 4:
Osserviamo che \(x = 0\) non è soluzione (il primo membro varrebbe \(-2 \neq 0\)). Per \(x \neq 0\) possiamo dividere per \(x\) e riscrivere:
\[ e^x + e^{-x} = \frac{2}{x} \]Confrontiamo graficamente \( g(x) = e^x + e^{-x} \) e \( h(x) = \dfrac{2}{x} \).
Proprietà di \( g(x) = e^x + e^{-x} \):
Proprietà di \( h(x) = \dfrac{2}{x} \):
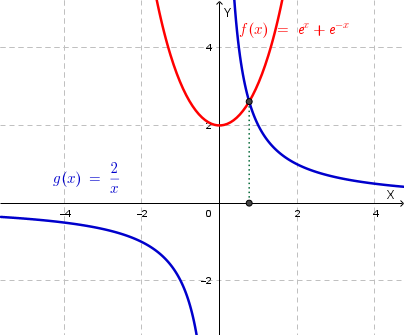
Le due curve si intersecano una sola volta, per \(x > 0\)
Per \(x < 0\): \(g(x) > 0\) mentre \(h(x) < 0\), quindi non ci sono intersezioni.
Per \(x > 0\): \(g(x)\) parte da 2 e cresce; \(h(x)\) parte da \(+\infty\) e decresce verso 0. Le due curve si intersecano esattamente una volta (compresa tra 0 e 2).
L'equazione ha una sola soluzione reale, positiva e compresa tra 0 e 2.
Data la retta \(r\) passante per \(A(1, 0, 2)\) e \(B(3, 2, 0)\) e il piano \(\pi: x + 2y + z = 6\):
Soluzione quesito 5:
Il vettore direzione di \(r\) ha componenti uguali alle differenze delle coordinate dei due punti:
\[ \vec{v} = (x_B - x_A,\; y_B - y_A,\; z_B - z_A) = (3-1,\; 2-0,\; 0-2) = (2, 2, -2) \]Le equazioni parametriche di \(r\), passante per \(A(1, 0, 2)\) con vettore direzione \(\vec{v}\), sono:
\[ \begin{cases} x = 1 + 2t \\ y = 2t \\ z = 2 - 2t \end{cases} \quad t \in \mathbb{R} \]Sostituiamo le equazioni parametriche nel piano \(x + 2y + z = 6\):
\[ (1 + 2t) + 2(2t) + (2 - 2t) = 6 \implies 3 + 4t = 6 \implies t = \frac{3}{4} \]Il punto di intersezione è:
\[ P = \left(1 + \frac{3}{2},\; \frac{3}{2},\; 2 - \frac{3}{2}\right) = \left(\frac{5}{2}, \frac{3}{2}, \frac{1}{2}\right) \]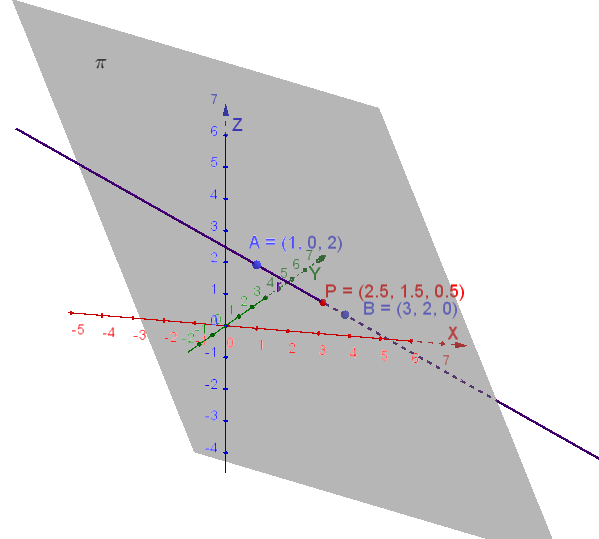
Figura 1: Intersezione retta-piano.
● Retta \(r\) |
■ Piano \(\pi\) |
● Punto \(P\)
Il raggio della sfera è la distanza \(PA\):
\[ r = |PA| = \sqrt{\left(\frac{5}{2}-1\right)^2 + \left(\frac{3}{2}-0\right)^2 + \left(\frac{1}{2}-2\right)^2} = \sqrt{\frac{9}{4} + \frac{9}{4} + \frac{9}{4}} = \sqrt{\frac{27}{4}} = \frac{3\sqrt{3}}{2} \]L'equazione della sfera è:
\[ \left(x - \frac{5}{2}\right)^2 + \left(y - \frac{3}{2}\right)^2 + \left(z - \frac{1}{2}\right)^2 = \frac{27}{4} \]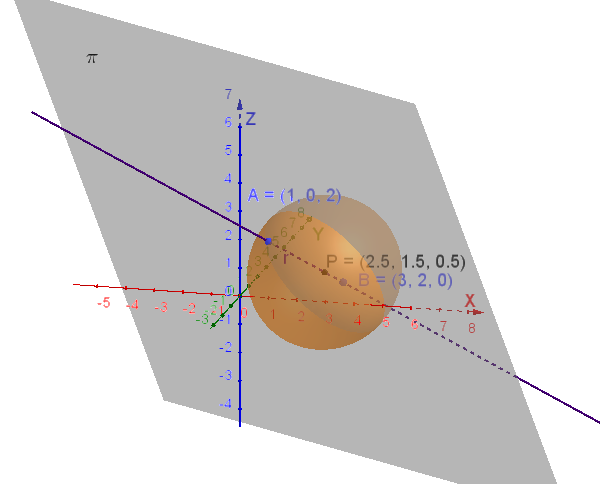
Figura 2: La sfera centrata nel punto di intersezione \(P\).
● Sfera: raggio \(R = \frac{3\sqrt{3}}{2}\).
● Punto \(A\): punto della superficie sferica.
Il triangolo \(PAH\), dove \(H\) è il piede della perpendicolare da \(A\) al piano \(\pi\), è rettangolo in \(H\). Quindi:
\[ \sin\alpha = \frac{AH}{AP} \]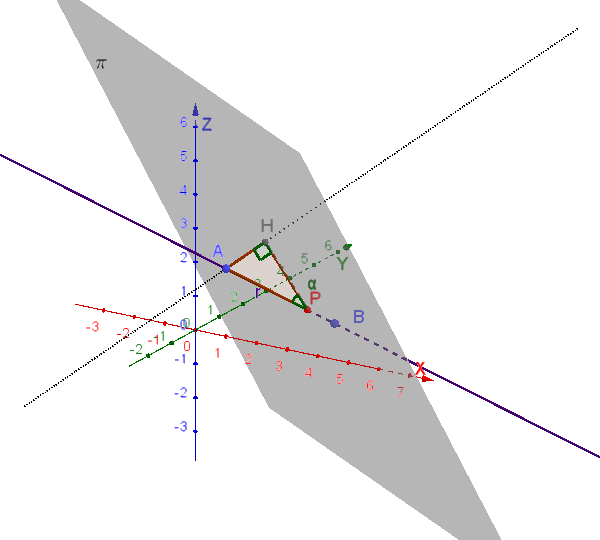
Figura 3: Costruzione dell'angolo \(\alpha\).
● Punto \(H\): proiezione di \(A\) sul piano.
⊿ Triangolo \(PAH\): evidenzia la relazione \(\sin\alpha = AH/AP\).
Calcoliamo \(AH\) con la formula della distanza punto-piano:
\[ AH = \frac{|x_A + 2y_A + z_A - 6|}{\sqrt{1^2 + 2^2 + 1^2}} = \frac{|1 + 0 + 2 - 6|}{\sqrt{6}} = \frac{3}{\sqrt{6}} = \frac{3\sqrt{6}}{6} = \frac{\sqrt{6}}{2} \]Il valore di \(AP\) è già noto dal Passo 3: \(AP = \dfrac{3\sqrt{3}}{2}\). Quindi:
\[ \sin\alpha = \frac{AH}{AP} = \frac{\dfrac{\sqrt{6}}{2}}{\dfrac{3\sqrt{3}}{2}} = \frac{\sqrt{6}}{3\sqrt{3}} = \frac{\sqrt{2}}{3} \]L'angolo tra la retta \(r\) e il piano \(\pi\) è:
\[ \alpha = \arcsin\!\left(\frac{\sqrt{2}}{3}\right) \approx 28°8' \]Calcolare l'area della regione di piano delimitata dalla parabola \(y = x^2 - 2x\) e dalla retta \(y = x\):
Soluzione quesito 6:
Risolviamo il sistema:
\[ x^2 - 2x = x \implies x^2 - 3x = 0 \implies x(x - 3) = 0 \]I punti di intersezione sono \(O(0, 0)\) e \(A(3, 3)\).
Nel tratto \([0, 3]\) la retta \(y = x\) sta sopra la parabola \(y = x^2 - 2x\).
In blu la parabola \(y = x^2 - 2x\), in verde la retta \(y = x\). La regione colorata è l'area da calcolare, compresa tra \(O(0,0)\) e \(A(3,3)\).
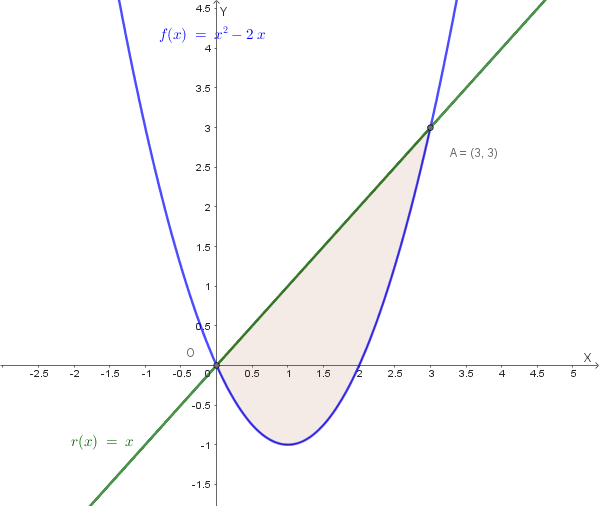
Fig. 1
Troviamo la tangente \(t\) alla parabola parallela alla retta \(y = x\), cioè con pendenza 1:
\[ y' = 2x - 2 = 1 \implies x = \frac{3}{2}, \quad y = \frac{9}{4} - 3 = -\frac{3}{4} \]Il punto di tangenza è \(T\!\left(\dfrac{3}{2},\, -\dfrac{3}{4}\right)\) e l'equazione della tangente è:
\[ t:\; y = x - \frac{9}{4} \quad \text{ovvero} \quad x - y - \frac{9}{4} = 0 \]In blu la parabola, in verde la retta \(y = x\), in rosso la tangente \(t\) nel punto \(T\!\left(\frac{3}{2}, -\frac{3}{4}\right)\). \(H\) è il piede della perpendicolare da \(T\) alla corda \(OA\), con \(h = TH\) altezza del rettangolo circoscritto.
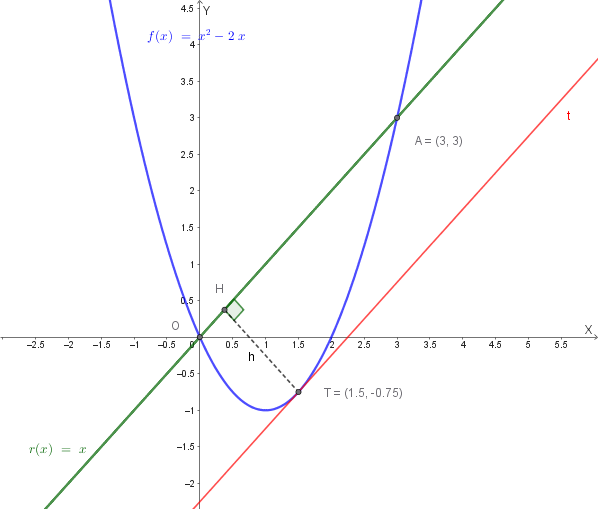
Fig. 2
La base del rettangolo circoscritto è la corda \(OA\):
\[ OA = \sqrt{(3-0)^2 + (3-0)^2} = \sqrt{18} = 3\sqrt{2} \]L'altezza del rettangolo circoscritto è la distanza di \(T\) dalla retta \(OA\), cioè dalla retta \(y = x\) ovvero \(x - y = 0\):
\[ h = \frac{\left|\dfrac{3}{2} - \left(-\dfrac{3}{4}\right)\right|}{\sqrt{2}} = \frac{\dfrac{9}{4}}{\sqrt{2}} = \frac{9}{4\sqrt{2}} = \frac{9\sqrt{2}}{8} \]L'area del segmento parabolico è \(\dfrac{2}{3}\) dell'area del rettangolo circoscritto:
\[ \text{Area} = \frac{2}{3} \cdot OA \cdot h = \frac{2}{3} \cdot 3\sqrt{2} \cdot \frac{9\sqrt{2}}{8} = \frac{2}{3} \cdot \frac{54}{8} = \frac{2}{3} \cdot \frac{27}{4} = \frac{9}{2} \]I due metodi concordano, confermando la validità del Teorema di Archimede per il segmento parabolico.
In una classe di 15 studenti (8 maschi e 7 femmine) si deve formare una commissione di 5 persone.
Soluzione quesito 7:
Il numero di commissioni di 5 persone scelte da 15 è dato dalla combinazione:
\[ \binom{15}{5} = \frac{15!}{5! \cdot 10!} = \frac{15 \cdot 14 \cdot 13 \cdot 12 \cdot 11}{5!} = \frac{360360}{120} = 3003 \]Usiamo il metodo del complementare: è più semplice contare le commissioni composte da soli maschi e sottrarle dal totale.
Commissioni composte da soli 5 maschi (scelti tra 8):
\[ \binom{8}{5} = \frac{8!}{5! \cdot 3!} = \frac{8 \cdot 7 \cdot 6}{3!} = \frac{336}{6} = 56 \]Commissioni con almeno una femmina:
\[ 3003 - 56 = 2947 \]Scegliamo 3 maschi tra 8 e 2 femmine tra 7, indipendentemente:
\[ \binom{8}{3} \cdot \binom{7}{2} = \frac{8 \cdot 7 \cdot 6}{3!} \cdot \frac{7 \cdot 6}{2!} = 56 \cdot 21 = 1176 \]Una volta formata la commissione di 5 persone, dobbiamo scegliere 2 di esse per ruoli distinti (presidente e segretario): si tratta quindi di una disposizione (l'ordine conta).
\[ D_{5,2} = 5 \cdot 4 = 20 \]Uno studente risponde a caso a 8 domande a risposta multipla, ciascuna con 4 opzioni di cui una sola corretta.
Soluzione quesito 8:
La probabilità di indovinare una risposta a caso è \(p = \dfrac{1}{4}\), quella di sbagliare è \(q = 1 - p = \dfrac{3}{4}\). Il numero di domande è \(n = 8\).
La variabile aleatoria \(X\) = numero di risposte corrette segue una distribuzione binomiale con formula generale:
\[ P(X = k) = \binom{8}{k} \left(\frac{1}{4}\right)^k \left(\frac{3}{4}\right)^{8-k} \]Usiamo il metodo del complementare:
\[ P(X \geq 2) = 1 - P(X = 0) - P(X = 1) \] \[ P(X = 0) = \binom{8}{0} \left(\frac{1}{4}\right)^0 \left(\frac{3}{4}\right)^8 = \frac{6561}{65536} \approx 0{,}1001 = 10{,}0\% \] \[ P(X = 1) = \binom{8}{1} \left(\frac{1}{4}\right)^1 \left(\frac{3}{4}\right)^7 = 8 \cdot \frac{1}{4} \cdot \frac{2187}{16384} = \frac{17496}{65536} \approx 0{,}2670 = 26{,}7\% \] \[ P(X \geq 2) = 1 - \frac{6561}{65536} - \frac{17496}{65536} = 1 - \frac{24057}{65536} = \frac{41479}{65536} \]Rispondere a caso dà meno del 3% di probabilità di prendere la sufficienza!