

Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.
Quesito 1
Dimostrare che l'equazione \(x^3 + x - \cos x = 0\) ammette un'unica soluzione. Dimostrare che tale soluzione è compresa tra 0 e 1 e trovare un valore approssimato a meno di un decimo utilizzando uno dei metodi numerici studiati.
Parte 1: Unicità della soluzione
Posto \(f(x) = x^3 + x - \cos x\) abbiamo:
\[ \lim_{x \to -\infty} f(x) = -\infty \quad \text{e} \quad \lim_{x \to +\infty} f(x) = +\infty \]
La derivata è:
\[ f'(x) = 3x^2 + 1 + \sin x > 0 \quad \text{per ogni } x \in \mathbb{R} \]
poiché \(3x^2 + 1 \geq 1\) e \(-1 \leq \sin x \leq 1\), con \(f'(x) = 0\) solo quando contemporaneamente \(x = 0\) e \(\sin x = -1\), il che non accade mai.
La funzione è quindi strettamente crescente su tutto \(\mathbb{R}\) e per il teorema dei valori intermedi ammette un'unica soluzione reale.
Parte 2: Localizzazione della soluzione in (0,1)
Calcoliamo:
\[ f(0) = 0^3 + 0 - \cos 0 = -1 < 0 \]
\[ f(1) = 1^3 + 1 - \cos 1 \approx 1 + 1 - 0.5403 = 1.4597 > 0 \]
Più precisamente:
\[ f(0.6) \approx 0.216 + 0.6 - 0.8253 \approx -0.0093 \]
\[ f(0.7) \approx 0.343 + 0.7 - 0.7648 \approx 0.2782 > 0 \]
Quindi la soluzione è in (0.6, 0.7)
Parte 3: Approssimazione con metodo di bisezione
Applicando il metodo di bisezione nell'intervallo [0.6,0.7]:
| Iterazione | a | b | Punto medio c | f(c) |
|---|---|---|---|---|
| 1 | 0.6 | 0.7 | 0.65 | 0.1254 |
| 2 | 0.6 | 0.65 | 0.625 | 0.0564 |
| 3 | 0.6 | 0.625 | 0.6125 | 0.0230 |
| 4 | 0.6 | 0.6125 | 0.60625 | 0.0067 |
Dopo 4 iterazioni, la soluzione è \(\alpha \approx 0.606\) con errore < 0.01
Parte 4: Approssimazione con metodo di Newton
Partendo da \(x_0 = 0.6\):
\[ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} = x_n - \frac{x_n^3 + x_n - \cos x_n}{3x_n^2 + 1 + \sin x_n} \]
| Iterazione | x_n | f(x_n) |
|---|---|---|
| 0 | 0.6 | -0.0093 |
| 1 | 0.6016 | 0.0001 |
Il metodo converge rapidamente a \(\alpha \approx 0.6016\)
Conclusione: L'equazione ha un'unica soluzione \(\alpha \in (0.6,0.7)\) e con entrambi i metodi otteniamo l'approssimazione \(\alpha \approx 0.6\) a meno di un decimo.
Quesito 2
Determinare il dominio della funzione \( f(x) = \ln\left(\frac{ax-7}{x^2}\right) \) con \( a \) parametro reale positivo.
Successivamente, individuare il valore di \( a \) in corrispondenza del quale risultano soddisfatte le ipotesi del teorema di Rolle nell'intervallo \([1,7]\) e le coordinate del punto che ne verifica la tesi.
Soluzione quesito 2:
Dominio: deve essere \( \frac{ax-7}{x^2} > 0 \), da cui: \( x > \frac{7}{a} \) (essendo \( a > 0 \)).
La funzione è continua e derivabile per ogni \( x > \frac{7}{a} \) con \( a > 0 \).
Applicazione del Teorema di Rolle:
Affinché valga il Teorema di Rolle nell'intervallo \([1,7]\) deve essere \( f(1) = f(7) \), quindi:
\[ \ln(a-7) = \ln\left(\frac{7a-7}{49}\right) \]
Da cui:
\[ a-7 = \frac{a-1}{7} \quad \Rightarrow \quad 7a-49 = a-1 \quad \Rightarrow \quad 6a = 48 \quad \Rightarrow \quad a = 8 \]
La funzione diventa quindi:
\[ f(x) = \ln\left(\frac{8x-7}{x^2}\right) \]
che è definita, continua e derivabile per \( x > \frac{7}{8} \).
Per \( a = 8 \) la funzione nell'intervallo \([1,7]\) soddisfa le tre ipotesi del Teorema di Rolle:
- Continua in \([1,7]\)
- Derivabile in \((1,7)\)
- \( f(1) = f(7) \)
Esiste quindi almeno un punto \( c \) interno all'intervallo in cui \( f'(c) = 0 \).
Calcoliamo la derivata:
\[ f'(x) = \frac{1}{\frac{8x-7}{x^2}} \cdot \frac{8x^2 - 2x(8x-7)}{x^4} = \frac{x^2}{8x-7} \cdot \frac{-8x^2 + 14x}{x^4} = \frac{-8x^2 + 14x}{x^2(8x-7)} \]
Ponendo \( f'(x) = 0 \):
\[ -8x^2 + 14x = 0 \quad \Rightarrow \quad x(8x - 14) = 0 \]
Soluzioni: \( x = 0 \) (non accettabile) e \( x = \frac{7}{4} = c \).
Calcoliamo \( f\left(\frac{7}{4}\right) \):
\[ f\left(\frac{7}{4}\right) = \ln\left(\frac{8 \cdot \frac{7}{4} - 7}{\left(\frac{7}{4}\right)^2}\right) = \ln\left(\frac{14-7}{\frac{49}{16}}\right) = \ln\left(\frac{16}{7}\right) \]
Le coordinate del punto che soddisfano il Teorema di Rolle in \([1,7]\) sono quindi:
\[ \left( \frac{7}{4}, \ln\left(\frac{16}{7}\right) \right) \]
Quesito 3
In un sistema di assi cartesiani Oxy, si consideri l'iperbole equilatera di equazione \(xy = k\), con \(k\) parametro reale non nullo. Sia \(t\) la retta tangente all'iperbole in un suo punto \(P\). Detti \(A\) e \(B\) i punti in cui \(t\) interseca gli assi del riferimento, dimostrare che i triangoli \(APO\) e \(BPO\) sono equivalenti e che la loro area non dipende dalla scelta di \(P\).
Soluzione quesito 3:
Sia \(P = (a, b)\) con \(ab = k\) il generico punto dell'iperbole. Utilizzando la formula di sdoppiamento otteniamo l'equazione della tangente \(t\) in \(P\) all'iperbole:
\[ \frac{ay + bx}{2} = k \quad \Rightarrow \quad bx + ay - 2k = 0 \]
Il punto \(A\), intersezione di \(t\) con l'asse delle \(y\) (x=0), ha coordinate:
\[ A = \left(0, \frac{2k}{a}\right) \]
Il punto \(B\), intersezione di \(t\) con l'asse delle \(x\) (y=0), ha coordinate:
\[ B = \left(\frac{2k}{b}, 0\right) \]
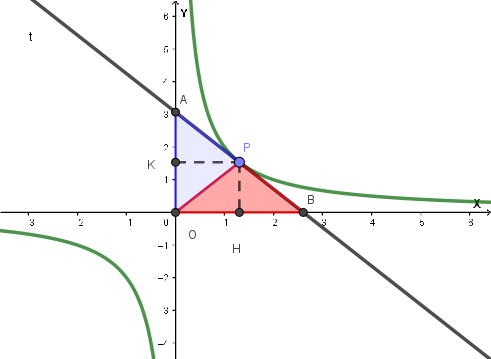
Calcoliamo le aree dei triangoli:
\[ \text{Area}(BPO) = \frac{OB \times PH}{2} = \frac{1}{2} \left|\frac{2k}{b}\right| \cdot |b| = |k| \]
\[ \text{Area}(APO) = \frac{OA \times PK}{2} = \frac{1}{2} \left|\frac{2k}{a}\right| \cdot |a| = |k| \]
Quindi i due triangoli sono equivalenti e la loro area non dipende dalla scelta di \(P\).
Dimostrazione alternativa con il metodo delle derivate:
A partire da \(xy = k\), con \(k \neq 0\), \(x \neq 0\) e \(y \neq 0\), consideriamo la funzione \(y = f(x) = \frac{k}{x}\).
Posto \(P = (a, b)\) con \(ab = k\), la tangente ha equazione:
\[ y - f(a) = f'(a)(x - a) \quad \Rightarrow \quad y - b = -\frac{k}{a^2}(x - a) \]
Intersezione con l'asse \(y\) (x=0):
\[ y = \frac{k}{a} + b \quad \Rightarrow \quad A = \left(0, \frac{k}{a} + b\right) \]
Intersezione con l'asse \(x\) (y=0):
\[ -b = -\frac{kx}{a^2} + \frac{k}{a} \quad \Rightarrow \quad x = \frac{a^2b}{k} + a \quad \Rightarrow \quad B = \left(\frac{a^2b}{k} + a, 0\right) \]
Calcoliamo nuovamente le aree:
\[ \text{Area}(BPO) = \frac{1}{2} \left|\frac{a^2b}{k} + a\right| \cdot |b| = \frac{1}{2} \left|\frac{a^2b^2}{k} + ab\right| = \frac{1}{2} \left|\frac{k^2}{k} + k\right| = |k| \]
\[ \text{Area}(APO) = \frac{1}{2} \left|\frac{k}{a} + b\right| \cdot |a| = \frac{1}{2} |k + ab| = \frac{1}{2} |k + k| = |k| \]
Come si può vedere, questo procedimento è meno veloce del primo.
N.B.
Esiste una proprietà dell'iperbole generica secondo cui l'area del triangolo formato dal centro dell'iperbole e dalle intersezioni della tangente in un qualsiasi punto \(P\) dell'iperbole con i suoi asintoti è costante al variare di \(P\). Nel nostro caso tale triangolo ha area costante \(|2k|\).
Quesito 4
Individuare e classificare i punti in cui la funzione \( f(x) = |x-1| + \sqrt[3]{x^3 + x^2} \) è continua ma non derivabile.
Soluzione quesito 4:
La funzione è definita e continua su tutto \(\mathbb{R}\). Studiamo la derivabilità.
Esprimiamo la funzione a tratti:
\[ f(x) = \begin{cases} x-1 + \sqrt[3]{x^3 + x^2} & \text{se } x \geq 1 \\ -x+1 + \sqrt[3]{x^3 + x^2} & \text{se } x < 1 \end{cases} \]
Calcoliamo la derivata:
\[ f'(x) = \begin{cases} 1 + \frac{3x^2 + 2x}{3\sqrt[3]{(x^3 + x^2)^2}} & \text{se } x > 1 \\ -1 + \frac{3x^2 + 2x}{3\sqrt[3]{(x^3 + x^2)^2}} & \text{se } x < 1 \end{cases} \]
La funzione non è derivabile quando \((x^3 + x^2)^2 = 0\), quindi per \(x = 0\) e \(x = -1\).
Analizziamo i limiti:
Per \(x \to 0^\pm\):
\[ \lim_{x \to 0^\pm} f'(x) = \lim_{x \to 0^\pm} \left(-1 + \frac{3x^2 + 2x}{3\sqrt[3]{(x^3 + x^2)^2}}\right) = \lim_{x \to 0} \left(-1 + \frac{2x}{3\sqrt[3]{x^4}}\right) = \pm\infty \]
Per \(x \to -1\):
\[ \lim_{x \to -1} f'(x) = \lim_{x \to -1} \left(-1 + \frac{3x^2 + 2x}{3\sqrt[3]{(x^3 + x^2)^2}}\right) = \left[-1 + \frac{1}{0^+}\right] = +\infty \]
La funzione non è derivabile anche in \(x = 1\):
\[ f'_+(1) = 1 + \frac{5}{3\sqrt[3]{4}} \quad \text{e} \quad f'_-(1) = -1 + \frac{5}{3\sqrt[3]{4}} \]
Quindi la funzione è continua su tutto \(\mathbb{R}\) ma non è derivabile nei punti \(x = -1\), \(x = 0\) e \(x = 1\).
Classificazione dei punti:
- \(x = -1\) è un punto di flesso a tangente verticale
- \(x = 0\) è un punto di cuspide
- \(x = 1\) è un punto angoloso
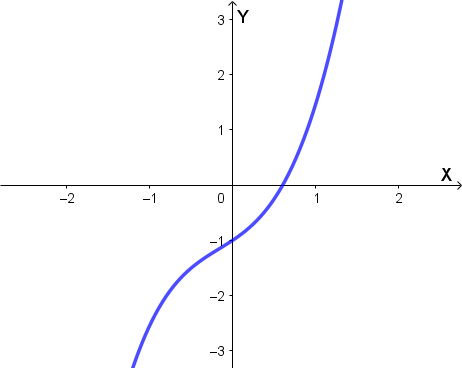
Grafico qualitativo della funzione:
Caratteristiche principali:
- x = -1: Flesso a tangente verticale (derivata infinita)
- x = 0: Cuspide (derivata sinistra e destra infinite ma di segno opposto)
- x = 1: Punto angoloso (derivata sinistra e destra finite ma diverse)
- La funzione è continua su tutto ℝ
- Comportamento asintotico: f(x) → ±∞ per x → ±∞