Risolvi da solo i singoli quesiti e controlla la soluzione premendo (una o due volte) il tasto corrispondente.
Quesito 1
Si consideri la funzione \[ f(x) = \frac{x + \sin x}{x - \cos x} \] Stabilire se si può calcolarne il limite per \(x \to +\infty\) e spiegare se il calcolo può essere effettuato ricorrendo al teorema di De L’Hôpital.
Quesito 2
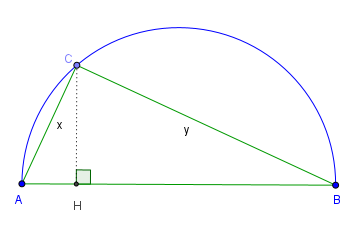
Dimostrare che tra tutti i triangoli inscritti in un semicerchio, quello isoscele ha area massima e perimetro massimo.
Quesito 3
Dimostrare che se p(x) è un polinomio, allora tra due qualsiasi radici distinte di p(x) c’è una radice di p’(x).
Quesito 4
Una classe è composta da 12 ragazzi e 4 ragazze. Tra i sedici allievi se ne scelgono 3 a caso: qual è la probabilità che essi siano tutti maschi?
Quesito 5
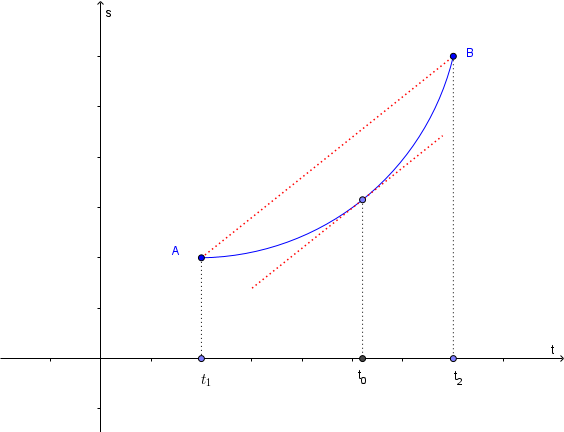
Dire, formalizzando la questione e utilizzando il teorema del valor medio o di Lagrange, se è vero che: «se un automobilista compie un viaggio senza soste in cui la velocità media è 60 km/h, allora almeno una volta durante il viaggio il tachimetro dell’automobile deve indicare esattamente 60 km/h».
Quesito 6
Nello spazio Oxyz sono date due rette \(r\) e \(s\).
La retta \(r\) è data in forma parametrica:
\[ r: \begin{cases} x = 1 + t \\ y = 2 - t \\ z = 3 + 2t \end{cases} \quad (t \in \mathbb{R}) \]La retta \(s\) è data come intersezione di due piani:
\[ s: \begin{cases} x + y - z = 0 \\ 2x - y + z = 1 \end{cases} \]Stabilire se le due rette \(r\) e \(s\) sono sghembe. Fornire una soluzione dettagliata.
Quesito 7
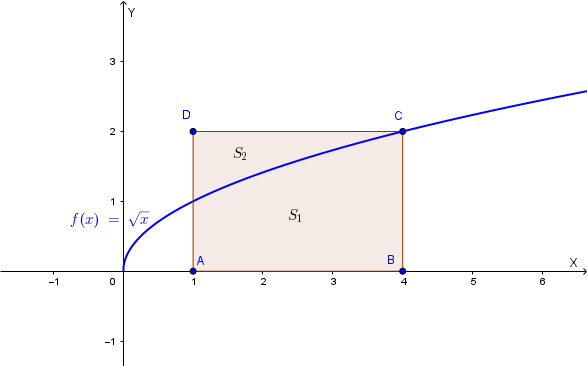
Il grafico della funzione \(f(x) = \sqrt{x}\) (\(x \in \mathbb{R}, x \ge 0\)) divide in due porzioni il rettangolo ABCD avente vertici A (1, 0), B (4, 0), C (4, 2) e D (1, 2). Calcolare il rapporto tra le aree delle due porzioni.
Quesito 8
Determinare il più piccolo valore del parametro reale \(k\) per cui la curva \(y = e^{2x} - 8e^{x} + k\) non ha punti nel semipiano \(y < 0\).
Dimostrare poi che la curva ha, per ogni valore di \(k\), un solo asintoto, di cui si chiede l'equazione.