

Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.
Quesito 1
Tre circonferenze di raggio 1 sono tangenti esternamente una all’altra. Qual è l’area della regione interna che esse delimitano?
Soluzione quesito 1:
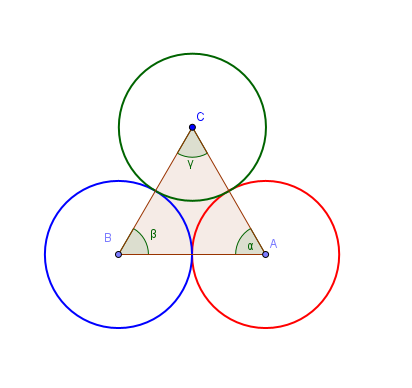
Osserviamo che il triangolo ABC che ha per vertici i centri delle tre circonferenze è un triangolo equilatero di lato 2 (per esempio AB, congiungente i centri di due circonferenze tangenti esternamente, passa per il punto di tangenza ed ha lunghezza pari alla somma dei due raggi; in modo analogo si ragiona per AC e BC). L’area \(S\) della regione delimitata dalle tre circonferenze ed esterna ad esse (triangolo curvilineo) si ottiene sottraendo all’area del triangolo ABC l’area di tre settori circolari di raggio 1 e ampiezza 60°; questi tre settori equivalgono ad un settore di raggio 1 e ampiezza 3x60°=180°, cioè ad un semicerchio di raggio 1, la cui area è quindi pari a \( \frac{\pi}{2} \). L’area del triangolo è uguale a \[ \text{Area}(ABC) = L^2 \cdot \frac{\sqrt{3}}{4} = 2^2 \cdot \frac{\sqrt{3}}{4} = 4 \cdot \frac{\sqrt{3}}{4} = \sqrt{3} \] Quindi l’area richiesta è: \[ S = \sqrt{3} - \frac{\pi}{2} \]
Quesito 2
In un’urna ci sono 20 biglie, ognuna delle quali è rossa o nera. Stabilire quante sono quelle nere, sapendo che estraendo 2 biglie senza riporre la prima estratta, la probabilità di estrarre almeno una biglia nera è 27/38.
Soluzione quesito 2:
Dette \(N\) le biglie nere, le biglie rosse \(R\) saranno \(20-N\). Detta \(p(RR)\) la probabilità di estrarre 2 biglie rosse, la probabilità \(p\) di estrarne almeno una nera è data da:
\[ p = 1 - p(RR) = 1 - \frac{(20-N)(19-N)}{20 \times 19} = 1 - \frac{(20-N)(19-N)}{380} \]Otteniamo quindi la seguente equazione:
\[ 1 - \frac{(20-N)(19-N)}{380} = \frac{27}{38} \]Risolviamo l'equazione:
\[ \frac{(20-N)(19-N)}{380} = 1 - \frac{27}{38} \] \[ \frac{(20-N)(19-N)}{380} = \frac{38-27}{38} \] \[ \frac{(20-N)(19-N)}{380} = \frac{11}{38} \]Moltiplichiamo entrambi i membri per 380:
\[ (20-N)(19-N) = \frac{11}{38} \times 380 \] \[ (20-N)(19-N) = 11 \times 10 \] \[ 380 - 20N - 19N + N^2 = 110 \] \[ N^2 - 39N + 380 - 110 = 0 \] \[ N^2 - 39N + 270 = 0 \]Risolviamo l'equazione di secondo grado per N utilizzando la formula risolutiva:
\[ N = \frac{-(-39) \pm \sqrt{(-39)^2 - 4(1)(270)}}{2(1)} \] \[ N = \frac{39 \pm \sqrt{1521 - 1080}}{2} \] \[ N = \frac{39 \pm \sqrt{441}}{2} \] \[ N = \frac{39 \pm 21}{2} \]Otteniamo due possibili soluzioni per N:
\[ N_1 = \frac{39 - 21}{2} = \frac{18}{2} = 9 \] \[ N_2 = \frac{39 + 21}{2} = \frac{60}{2} = 30 \]Poiché il numero totale di biglie è 20, la soluzione \(N_2 = 30\) non è accettabile.
Dovendo essere 20 tutte le biglie, quelle nere saranno **9**.
Quesito 3
Posto, per \(n \in \mathbb{N}\), \(I_n = \int_0^1 x^n e^x dx\), stabilire il valore di \(I_0\) e dimostrare che, per ogni \(n \in \mathbb{N}\), si ha \(I_n = e - n I_{n-1}\).
Soluzione quesito 3:
Per stabilire il valore di \(I_0\):
\[ I_0 = \int_0^1 x^0 e^x dx = \int_0^1 e^x dx = [e^x]_0^1 = e^1 - e^0 = e - 1 \]Dimostriamo che, per ogni \(n \in \mathbb{N}\), si ha \(I_n = e - n I_{n-1}\).
Integrando per parti l'espressione di \(I_n\), con \(f(x) = x^n\) e \(g'(x) = e^x\):
\(f'(x) = nx^{n-1}\), \(g(x) = e^x\).
\[ I_n = \int_0^1 x^n e^x dx = [x^n e^x]_0^1 - \int_0^1 nx^{n-1} e^x dx \] \[ I_n = (1^n e^1 - 0^n e^0) - n \int_0^1 x^{n-1} e^x dx \] \[ I_n = (1 \cdot e - 0) - n I_{n-1} \] \[ I_n = e - n I_{n-1} \]La dimostrazione è così completata.
Quesito 4
Si considerino nello spazio il punto \(P(1,2,-1)\) ed il piano \(\alpha\) di equazione \(x-2y+z+4=0\).
a) Verificare che \(P \in \alpha\);
b) determinare le equazioni delle superfici sferiche di raggio 6 che sono tangenti ad \(\alpha\) in P.
Soluzione quesito 4:
a) Per verificare che \(P \in \alpha\), sostituiamo le coordinate di \(P(1,2,-1)\) nell'equazione del piano \(\alpha\):
\[ 1 - 2(2) + (-1) + 4 = 1 - 4 - 1 + 4 = 0 \]Poiché il risultato è 0, le coordinate di \(P\) soddisfano l'equazione del piano. Quindi, \(P \in \alpha\).
b) I centri delle sfere richieste appartengono alla retta \(n\) perpendicolare al piano \(\alpha\) e passante per \(P\). I parametri direttori della retta \(n\) sono i coefficienti dei termini \(x, y, z\) dell'equazione del piano, cioè \((1, -2, 1)\).
La retta \(n\) ha quindi equazioni parametriche:
\[ \begin{cases} x = 1 + t \\ y = 2 - 2t \\ z = -1 + t \end{cases} \]Posto \(C=(1+t, 2-2t, -1+t)\) un generico punto sulla retta \(n\) (e quindi un potenziale centro della sfera), il raggio delle sfere richieste è dato dalla distanza \(CP\). Deve quindi essere:
\[ CP^2 = 6^2 = 36 \]Applichiamo la formula della distanza tra due punti \(C(1+t, 2-2t, -1+t)\) e \(P(1,2,-1)\):
\[ ( (1+t) - 1 )^2 + ( (2-2t) - 2 )^2 + ( (-1+t) - (-1) )^2 = 36 \] \[ (t)^2 + (-2t)^2 + (t)^2 = 36 \] \[ t^2 + 4t^2 + t^2 = 36 \] \[ 6t^2 = 36 \] \[ t^2 = 6 \] \[ t = \pm\sqrt{6} \]I centri delle sfere sono quindi:
Per \(t = \sqrt{6}\):
\[ C_1 = (1+\sqrt{6}, 2-2\sqrt{6}, -1+\sqrt{6}) \]Per \(t = -\sqrt{6}\):
\[ C_2 = (1-\sqrt{6}, 2+2\sqrt{6}, -1-\sqrt{6}) \]Le sfere richieste hanno quindi equazioni (forma \( (x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2 = r^2 \)):
\[ [x - (1 \pm \sqrt{6})]^2 + [y - (2 \mp 2\sqrt{6})]^2 + [z - (-1 \pm \sqrt{6})]^2 = 36 \]Dove il segno superiore \((+)\) corrisponde al centro \(C_1\) e il segno inferiore \( (-)\) corrisponde al centro \(C_2\).
Quesito 5
Data la funzione così definita in \(\mathbb{R}\):
\[ f(x) = x \cdot e^{-|x^3-1|} \]determinarne minimi, massimi ed eventuali asintoti.
Soluzione quesito 5:
Il **dominio** della funzione è \(D = \mathbb{R}\), poiché \(e^u\) è definita per ogni \(u \in \mathbb{R}\) e \(|x^3-1|\) è sempre definita.
Asintoti
La funzione è continua su tutto \(\mathbb{R}\), quindi non ci sono asintoti verticali.
Per gli **asintoti orizzontali**, calcoliamo i limiti per \(x \to \pm\infty\):
\[ \lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} x \cdot e^{-|x^3-1|} = \lim_{x \to +\infty} x \cdot e^{-(x^3-1)} = \lim_{x \to +\infty} \frac{x}{e^{x^3-1}} = 0 \]Quindi, la retta \(y=0\) è un **asintoto orizzontale** per \(x \to +\infty\).
\[ \lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} x \cdot e^{-|x^3-1|} = \lim_{x \to -\infty} x \cdot e^{-(-(x^3-1))} = \lim_{x \to -\infty} x \cdot e^{x^3-1} = 0 \]Anche per \(x \to -\infty\), la retta \(y=0\) è un **asintoto orizzontale**.
Non ci sono asintoti obliqui poiché ci sono asintoti orizzontali.
Minimi e Massimi
La funzione può essere scritta a tratti, eliminando il modulo:
\[ f(x) = \begin{cases} x \cdot e^{-(x^3-1)} & \text{se } x^3-1 \ge 0 \Rightarrow x^3 \ge 1 \Rightarrow x \ge 1 \\ x \cdot e^{-(-(x^3-1))} = x \cdot e^{x^3-1} & \text{se } x^3-1 < 0 \Rightarrow x^3 < 1 \Rightarrow x < 1 \end{cases} \]Calcoliamo la **derivata prima** \(f'(x)\).
Per \(x > 1\): \(f(x) = x \cdot e^{1-x^3}\)
\[ f'(x) = 1 \cdot e^{1-x^3} + x \cdot e^{1-x^3} \cdot (-3x^2) = e^{1-x^3}(1 - 3x^3) \]Per \(x > 1\), \(e^{1-x^3} > 0\). Il segno di \(f'(x)\) dipende da \(1 - 3x^3\).
\[ 1 - 3x^3 = 0 \Rightarrow 3x^3 = 1 \Rightarrow x^3 = \frac{1}{3} \Rightarrow x = \sqrt[3]{\frac{1}{3}} \]Dato che \(x > 1\), \(1-3x^3\) sarà sempre negativo (ad esempio, per \(x=2\), \(1-3(8) = -23 < 0\)). Quindi, per \(x > 1\), \(f'(x) < 0\), e la funzione è **decrescente**.
Per \(x < 1\): \(f(x) = x \cdot e^{x^3-1}\)
\[ f'(x) = 1 \cdot e^{x^3-1} + x \cdot e^{x^3-1} \cdot (3x^2) = e^{x^3-1}(1 + 3x^3) \]Per \(x < 1\), \(e^{x^3-1} > 0\). Il segno di \(f'(x)\) dipende da \(1 + 3x^3\).
\[ 1 + 3x^3 = 0 \Rightarrow 3x^3 = -1 \Rightarrow x^3 = -\frac{1}{3} \Rightarrow x = \sqrt[3]{-\frac{1}{3}} = -\frac{1}{\sqrt[3]{3}} \]Studiamo il segno di \(1+3x^3\):
- Se \(x < -\frac{1}{\sqrt[3]{3}}\), allora \(1+3x^3 < 0\), quindi \(f'(x) < 0\). La funzione è **decrescente**.
- Se \(-\frac{1}{\sqrt[3]{3}} < x < 1\), allora \(1+3x^3 > 0\), quindi \(f'(x) > 0\). La funzione è **crescente**.
Analizziamo il comportamento in \(x=1\).
Per \(x \to 1^-\), \(f'(x) = e^{x^3-1}(1+3x^3) \to e^0(1+3) = 4\).
Per \(x \to 1^+\), \(f'(x) = e^{1-x^3}(1-3x^3) \to e^0(1-3) = -2\).
Poiché le derivate sinistra e destra in \(x=1\) sono diverse, \(x=1\) è un **punto angoloso**.
Globalmente:
- Per \(x < -\frac{1}{\sqrt[3]{3}}\): \(f(x)\) è decrescente.
- Per \(-\frac{1}{\sqrt[3]{3}} < x < 1\): \(f(x)\) è crescente.
- Per \(x > 1\): \(f(x)\) è decrescente.
Deduciamo che:
- In \(x = -\frac{1}{\sqrt[3]{3}}\) c'è un **minimo relativo**.
- In \(x = 1\) c'è un **massimo relativo** (punto angoloso).
Calcoliamo i valori della funzione in questi punti:
Per il minimo relativo a \(x = -\frac{1}{\sqrt[3]{3}}\):
\[ f\left(-\frac{1}{\sqrt[3]{3}}\right) = -\frac{1}{\sqrt[3]{3}} \cdot e^{-|(-\frac{1}{\sqrt[3]{3}})^3-1|} = -\frac{1}{\sqrt[3]{3}} \cdot e^{-|-\frac{1}{3}-1|} = -\frac{1}{\sqrt[3]{3}} \cdot e^{-|-\frac{4}{3}|} = -\frac{1}{\sqrt[3]{3}} e^{-\frac{4}{3}} \]Per il massimo relativo a \(x = 1\):
\[ f(1) = 1 \cdot e^{-|1^3-1|} = 1 \cdot e^{-|0|} = 1 \cdot e^0 = 1 \]Riepilogando:
- **Asintoto orizzontale:** \(y=0\) per \(x \to \pm\infty\).
- **Minimo assoluto:** \(x = -\frac{1}{\sqrt[3]{3}}\) con ordinata \(f\left(-\frac{1}{\sqrt[3]{3}}\right) = -\frac{1}{\sqrt[3]{3}} e^{-\frac{4}{3}}\).
- **Massimo assoluto:** \(x = 1\) con ordinata \(f(1) = 1\).
- Questo perché i valori della funzione si avvicinano a zero per \(x \to \pm\infty\), e i punti critici rappresentano gli estremi globali.
Quesito 6
Dato \(k > 0\), si consideri la funzione \(f: [0, +\infty) \to \mathbb{R}\) così definita:
\[ f(x) = \begin{cases} kx & \text{se } 0 \le x \le 1 \\ \frac{k}{x^2} & \text{se } x > 1 \end{cases} \]a) Dimostrare che, qualunque sia \(k > 0\), la funzione \(f\) è continua ma non ovunque derivabile.
b) Per quali valori di \(k\) le tangenti destra e sinistra nel punto di non derivabilità formano un angolo acuto \(\gamma\) tale che \(\tan \gamma = 3\)?
Soluzione a)
Per \(x \neq 1\) la funzione è continua (è una retta o una razionale il cui denominatore non si annulla). Analizziamo la continuità in \(x=1\).
\[ f(1) = k \cdot 1 = k \] \[ \lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} (kx) = k \] \[ \lim_{x \to 1^+} f(x) = \lim_{x \to 1^+} \left(\frac{k}{x^2}\right) = \frac{k}{1^2} = k \]Poiché \(f(1) = \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x)\), la funzione è **continua per ogni valore di \(k\)**.
Analizziamo la derivabilità. Anche in questo caso il punto da analizzare è \(x=1\), essendo la funzione derivabile per \(x \neq 1\).
Calcoliamo la derivata \(f'(x)\):
\[ f'(x) = \begin{cases} k & \text{se } 0 \le x < 1 \\ -2kx^{-3} & \text{se } x > 1 \end{cases} \] \[ f'(x) = \begin{cases} k & \text{se } 0 \le x < 1 \\ -\frac{2k}{x^3} & \text{se } x > 1 \end{cases} \]Calcoliamo la derivata sinistra e destra in \(x=1\):
\[ \lim_{x \to 1^-} f'(x) = \lim_{x \to 1^-} (k) = k \] \[ \lim_{x \to 1^+} f'(x) = \lim_{x \to 1^+} \left(-\frac{2k}{x^3}\right) = -\frac{2k}{1^3} = -2k \]Perché la funzione sia derivabile in \(x=1\), le derivate destra e sinistra dovrebbero essere uguali: \(k = -2k\). Questo implica \(3k=0\), ovvero \(k=0\).
Dato che il problema specifica \(k > 0\), per ogni \(k>0\) risulta \(k \neq -2k\). Quindi, per \(k > 0\), la funzione **non è derivabile in \(x=1\)**.
Soluzione b)
Consideriamo il punto di non derivabilità \(P=(1, k)\).
Le pendenze delle tangenti destra e sinistra in \(x=1\) sono le derivate destra e sinistra che abbiamo già calcolato:
\[ m_1 = f'_-(1) = k \] \[ m_2 = f'_+(1) = -2k \]Detto \(\gamma\) l'angolo tra le tangenti destra e sinistra in \(P\), la tangente di \(\gamma\) è data dalla formula:
\[ \tan \gamma = \left|\frac{m_1 - m_2}{1 + m_1 m_2}\right| \]Sostituendo i valori delle pendenze:
\[ \tan \gamma = \left|\frac{k - (-2k)}{1 + k(-2k)}\right| = \left|\frac{k + 2k}{1 - 2k^2}\right| = \left|\frac{3k}{1 - 2k^2}\right| \]Ci viene richiesto che \(\tan \gamma = 3\), quindi dobbiamo risolvere l'equazione:
\[ \left|\frac{3k}{1 - 2k^2}\right| = 3 \]Questo porta a due casi:
Caso 1: \(\frac{3k}{1 - 2k^2} = 3\)
\[ 3k = 3(1 - 2k^2) \] \[ 3k = 3 - 6k^2 \] \[ 6k^2 + 3k - 3 = 0 \]Dividiamo per 3:
\[ 2k^2 + k - 1 = 0 \]Risolviamo per \(k\) usando la formula quadratica:
\[ k = \frac{-1 \pm \sqrt{1^2 - 4(2)(-1)}}{2(2)} = \frac{-1 \pm \sqrt{1 + 8}}{4} = \frac{-1 \pm \sqrt{9}}{4} = \frac{-1 \pm 3}{4} \]Le soluzioni sono:
\[ k_1 = \frac{-1 - 3}{4} = \frac{-4}{4} = -1 \quad \text{(Non accettabile, poiché } k > 0 \text{)} \] \[ k_2 = \frac{-1 + 3}{4} = \frac{2}{4} = \frac{1}{2} \quad \text{(Accettabile)} \]Caso 2: \(\frac{3k}{1 - 2k^2} = -3\)
\[ 3k = -3(1 - 2k^2) \] \[ 3k = -3 + 6k^2 \] \[ 6k^2 - 3k - 3 = 0 \]Dividiamo per 3:
\[ 2k^2 - k - 1 = 0 \]Risolviamo per \(k\) usando la formula quadratica:
\[ k = \frac{-(-1) \pm \sqrt{(-1)^2 - 4(2)(-1)}}{2(2)} = \frac{1 \pm \sqrt{1 + 8}}{4} = \frac{1 \pm \sqrt{9}}{4} = \frac{1 \pm 3}{4} \]Le soluzioni sono:
\[ k_3 = \frac{1 - 3}{4} = \frac{-2}{4} = -\frac{1}{2} \quad \text{(Non accettabile, poiché } k > 0 \text{)} \] \[ k_4 = \frac{1 + 3}{4} = \frac{4}{4} = 1 \quad \text{(Accettabile)} \]Pertanto, le tangenti destra e sinistra nel punto di non derivabilità formano un angolo acuto \(\gamma\) tale che \(\tan \gamma = 3\) se \(k = \frac{1}{2}\) o \(k = 1\).
Quesito 7
Per il progetto di una piscina, un architetto si ispira alle funzioni \(f\) e \(g\) definite, per tutti gli \(x\) reali, da:
\[ f(x) = x^3 - 16x \quad \text{e} \quad g(x) = \sin\left(\frac{\pi}{2}x\right) \]L’architetto rappresenta la superficie libera dell’acqua nella piscina con la regione \(R\) delimitata dai grafici di \(f\) e di \(g\) sull’intervallo \([0; 4]\).
Dopo aver rappresentato qualitativamente nello stesso sistema di riferimento le due funzioni, si chiede di trovare:
a) L'area della regione \(R\).
b) Sapendo che in ogni punto di \(R\) a distanza \(x\) dall’asse \(y\), la misura della profondità dell’acqua nella piscina è data da \(h(x) = 5 – x\), quale sarà il volume d’acqua nella piscina?
Soluzione quesito 7:
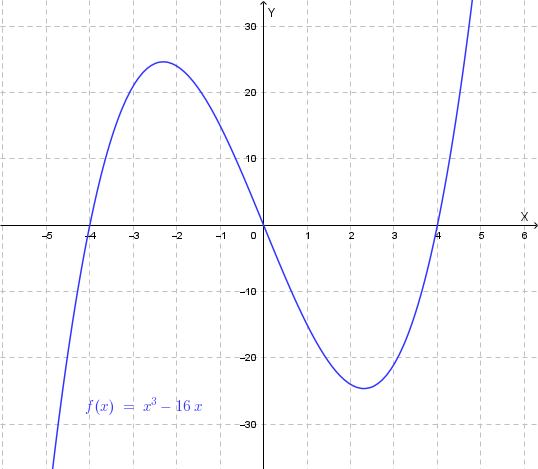
Studio qualitativo di \(f(x)=x^3 - 16x\):
Si tratta di una funzione cubica definita su tutto \(\mathbb{R}\). Per uno studio qualitativo, è sufficiente analizzare i suoi limiti agli infiniti e le intersezioni con gli assi cartesiani.
Limiti:
\[ \lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} (x^3 - 16x) = +\infty \] \[ \lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} (x^3 - 16x) = -\infty \]Intersezioni con l'asse x (ponendo \(f(x)=0\)):
\[ x^3 - 16x = 0 \Rightarrow x(x^2 - 16) = 0 \Rightarrow x(x-4)(x+4) = 0 \]Le intersezioni sono in \(x=0\), \(x=4\) e \(x=-4\).
Intersezione con l'asse y (ponendo \(x=0\)):
\[ f(0) = 0^3 - 16(0) = 0 \]Quindi l'origine \((0,0)\) è l'unica intersezione con l'asse y.
La funzione è simmetrica rispetto all’origine, dato che \(f(-x) = (-x)^3 - 16(-x) = -x^3 + 16x = -f(x)\).
Il grafico qualitativo di \(f(x)\) è il seguente:
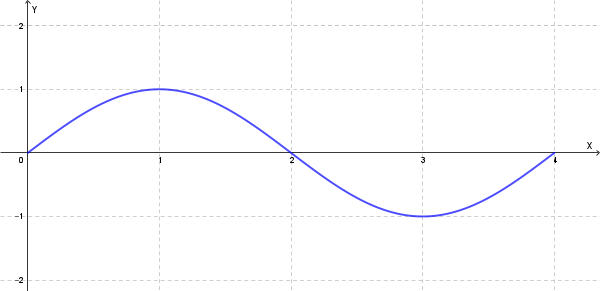
Studio di \(g(x)=\sin\left(\frac{\pi}{2}x\right)\):
Si tratta di una funzione sinusoidale. Il periodo \(T\) è dato da \(T = \frac{2\pi}{\omega}\), dove \(\omega = \frac{\pi}{2}\). Quindi \(T = \frac{2\pi}{\frac{\pi}{2}} = 4\).
Il suo grafico in \([0; 4]\) è il seguente:
Rappresentiamo la regione R richiesta:
La regione \(R\) è delimitata dai grafici di \(f(x)\) e \(g(x)\) sull'intervallo \([0; 4]\).
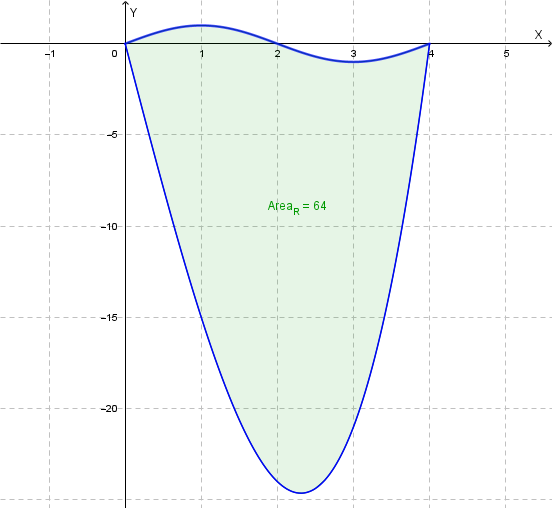
a) Area della regione R:
Dall'analisi dei grafici sull'intervallo \([0, 4]\), si osserva che \(g(x) \ge f(x)\).
L'area della regione \(R\) richiesta si ottiene calcolando l'integrale definito:
\[ \text{Area}(R) = \int_0^4 (g(x) - f(x)) dx = \int_0^4 \left( \sin\left(\frac{\pi}{2}x\right) - (x^3 - 16x) \right) dx \] \[ \text{Area}(R) = \int_0^4 \sin\left(\frac{\pi}{2}x\right) dx - \int_0^4 (x^3 - 16x) dx \]Calcoliamo il primo integrale:
\[ \int_0^4 \sin\left(\frac{\pi}{2}x\right) dx = \left[ -\frac{2}{\pi}\cos\left(\frac{\pi}{2}x\right) \right]_0^4 \] \[ = -\frac{2}{\pi}\cos\left(\frac{\pi}{2}\cdot 4\right) - \left(-\frac{2}{\pi}\cos\left(\frac{\pi}{2}\cdot 0\right)\right) \] \[ = -\frac{2}{\pi}\cos(2\pi) + \frac{2}{\pi}\cos(0) = -\frac{2}{\pi}(1) + \frac{2}{\pi}(1) = 0 \]Calcoliamo il secondo integrale:
\[ \int_0^4 (x^3 - 16x) dx = \left[ \frac{x^4}{4} - 8x^2 \right]_0^4 \] \[ = \left( \frac{4^4}{4} - 8(4^2) \right) - \left( \frac{0^4}{4} - 8(0^2) \right) \] \[ = \left( \frac{256}{4} - 8 \cdot 16 \right) - 0 = (64 - 128) = -64 \]Quindi l'Area di R è:
\[ \text{Area}(R) = 0 - (-64) = 64 \]L'area è \(64\).
b) Calcolo del volume:
Il volume richiesto si calcola mediante l'integrale definito:
\[ V = \int_0^4 (g(x) - f(x)) h(x) dx \]Poiché può essere visto come somma di infiniti parallelepipedi elementari (o "fette") con area di base \((g(x)-f(x))\) e altezza \(h(x)\), estesa sull'intervallo \([0;4]\).
L'integrale da calcolare è il seguente:
\[ V = \int_0^4 \left( \sin\left(\frac{\pi}{2}x\right) - (x^3 - 16x) \right) (5-x) dx \] \[ V = \int_0^4 \left( 5\sin\left(\frac{\pi}{2}x\right) - x\sin\left(\frac{\pi}{2}x\right) - (5x^3 - 80x - x^4 + 16x^2) \right) dx \] \[ V = \int_0^4 (5\sin\left(\frac{\pi}{2}x\right) - x\sin\left(\frac{\pi}{2}x\right)) dx + \int_0^4 (x^4 - 5x^3 - 16x^2 + 80x) dx \]Calcoliamo il secondo integrale (parte polinomiale):
\[ \int_0^4 (x^4 - 5x^3 - 16x^2 + 80x) dx = \left[ \frac{x^5}{5} - \frac{5x^4}{4} - \frac{16x^3}{3} + 40x^2 \right]_0^4 \] \[ = \left( \frac{4^5}{5} - \frac{5 \cdot 4^4}{4} - \frac{16 \cdot 4^3}{3} + 40 \cdot 4^2 \right) - 0 \] \[ = \frac{1024}{5} - 320 - \frac{1024}{3} + 640 \] \[ = \frac{1024}{5} + 320 - \frac{1024}{3} = \frac{3 \cdot 1024 + 15 \cdot 320 - 5 \cdot 1024}{15} \] \[ = \frac{3072 + 4800 - 5120}{15} = \frac{2752}{15} \]Calcoliamo il primo integrale (parte sinusoidale), che richiede integrazione per parti per il termine \(x\sin\left(\frac{\pi}{2}x\right)\):
\[ \int_0^4 (5\sin\left(\frac{\pi}{2}x\right) - x\sin\left(\frac{\pi}{2}x\right)) dx \] \[ = 5 \int_0^4 \sin\left(\frac{\pi}{2}x\right) dx - \int_0^4 x\sin\left(\frac{\pi}{2}x\right) dx \]Sappiamo già che \(5 \int_0^4 \sin\left(\frac{\pi}{2}x\right) dx = 5 \cdot 0 = 0\).
Per \(\int x\sin\left(\frac{\pi}{2}x\right) dx\), usiamo integrazione per parti: \(\int u dv = uv - \int v du\). Scegliamo \(u=x\) e \(dv=\sin\left(\frac{\pi}{2}x\right)dx\).
Allora \(du=dx\) e \(v = -\frac{2}{\pi}\cos\left(\frac{\pi}{2}x\right)\).
\[ \int_0^4 x\sin\left(\frac{\pi}{2}x\right) dx = \left[ -x\frac{2}{\pi}\cos\left(\frac{\pi}{2}x\right) \right]_0^4 - \int_0^4 \left(-\frac{2}{\pi}\cos\left(\frac{\pi}{2}x\right)\right) dx \] \[ = \left( -4\frac{2}{\pi}\cos(2\pi) - 0 \right) + \frac{2}{\pi}\int_0^4 \cos\left(\frac{\pi}{2}x\right) dx \] \[ = -\frac{8}{\pi}(1) + \frac{2}{\pi}\left[ \frac{2}{\pi}\sin\left(\frac{\pi}{2}x\right) \right]_0^4 \] \[ = -\frac{8}{\pi} + \frac{4}{\pi^2}\left( \sin(2\pi) - \sin(0) \right) = -\frac{8}{\pi} + \frac{4}{\pi^2}(0 - 0) = -\frac{8}{\pi} \]Quindi la parte sinusoidale è \(0 - (-\frac{8}{\pi}) = \frac{8}{\pi}\).
Il volume totale è la somma delle due parti:
\[ V = \frac{8}{\pi} + \frac{2752}{15} \]Calcolando il valore numerico approssimato:
\[ V \approx \frac{8}{3.14159} + \frac{2752}{15} \approx 2.546 + 183.467 \approx 186.013 \]Il volume d'acqua nella piscina è circa \(186.013\).
Quesito 8
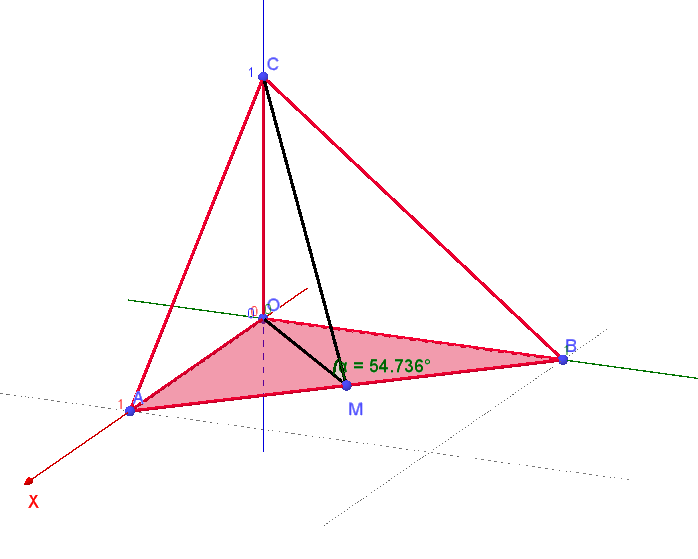
Nello spazio tridimensionale \(Oxyz\) si consideri il tetraedro di vertici \(O=(0,0,0)\), \(A=(1,0,0)\), \(B=(0,1,0)\) e \(C=(0,0,1)\).
a) Si calcolino la superficie totale ed il volume del tetraedro.
b) Si calcoli l'angolo in gradi che la faccia \(ABC\) forma con la base \(OAB\).
Soluzione quesito 8:
a) Calcolo della superficie totale e del volume del tetraedro
Il tetraedro ha quattro facce triangolari e sei spigoli (lati).
Calcolo dell'area delle facce:
Le facce sono triangoli. Per i triangoli rettangoli, l'area è data da \(\frac{1}{2} \cdot \text{base} \cdot \text{altezza}\). Per la faccia \(ABC\), che è un triangolo equilatero, useremo la formula specifica.
- **Faccia OAB (Base):** Vertici \(O(0,0,0)\), \(A(1,0,0)\), \(B(0,1,0)\). Questo è un triangolo rettangolo con i cateti sugli assi \(x\) e \(y\). \[ \text{Area}_{OAB} = \frac{1}{2} \cdot OA \cdot OB = \frac{1}{2} \cdot 1 \cdot 1 = \frac{1}{2} \]
- **Faccia OAC:** Vertici \(O(0,0,0)\), \(A(1,0,0)\), \(C(0,0,1)\). Questo è un triangolo rettangolo con i cateti sugli assi \(x\) e \(z\). \[ \text{Area}_{OAC} = \frac{1}{2} \cdot OA \cdot OC = \frac{1}{2} \cdot 1 \cdot 1 = \frac{1}{2} \]
- **Faccia OBC:** Vertici \(O(0,0,0)\), \(B(0,1,0)\), \(C(0,0,1)\). Questo è un triangolo rettangolo con i cateti sugli assi \(y\) e \(z\). \[ \text{Area}_{OBC} = \frac{1}{2} \cdot OB \cdot OC = \frac{1}{2} \cdot 1 \cdot 1 = \frac{1}{2} \]
- **Faccia ABC:** Vertici \(A(1,0,0)\), \(B(0,1,0)\), \(C(0,0,1)\). Per determinare il tipo di triangolo, calcoliamo le lunghezze dei suoi lati (spigoli):
- \(AB = \sqrt{(0-1)^2 + (1-0)^2 + (0-0)^2} = \sqrt{1 + 1} = \sqrt{2}\)
- \(AC = \sqrt{(0-1)^2 + (0-0)^2 + (1-0)^2} = \sqrt{1 + 1} = \sqrt{2}\)
- \(BC = \sqrt{(0-0)^2 + (0-1)^2 + (1-0)^2} = \sqrt{1 + 1} = \sqrt{2}\)
Poiché tutti i lati sono lunghi \(\sqrt{2}\), la faccia \(ABC\) è un **triangolo equilatero**. L'area di un triangolo equilatero di lato \(L\) è data da \(\frac{\sqrt{3}}{4}L^2\).
\[ \text{Area}_{ABC} = \frac{\sqrt{3}}{4} (\sqrt{2})^2 = \frac{\sqrt{3}}{4} \cdot 2 = \frac{\sqrt{3}}{2} \]
Superficie totale:
La **superficie totale** è la somma delle aree delle quattro facce:
\[ \text{Superficie Totale} = \text{Area}_{OAB} + \text{Area}_{OAC} + \text{Area}_{OBC} + \text{Area}_{ABC} \] \[ \text{Superficie Totale} = \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{\sqrt{3}}{2} = \frac{3 + \sqrt{3}}{2} \] \[ \text{Superficie Totale} \approx \frac{3 + 1.732}{2} = \frac{4.732}{2} = 2.366 \]Calcolo del volume del tetraedro:
Il volume di un tetraedro può essere calcolato con la formula: \(V = \frac{1}{3} \cdot \text{Area}_{\text{Base}} \cdot \text{altezza}\).
Possiamo considerare la faccia \(OAB\) come base. L'area della base \(OAB\) è \(\frac{1}{2}\).
L'altezza del tetraedro rispetto alla base \(OAB\) è la distanza del vertice \(C(0,0,1)\) dal piano contenente la base \(OAB\). Il piano \(OAB\) è il piano \(xy\), la cui equazione è \(z=0\).
La distanza di \(C(0,0,1)\) dal piano \(z=0\) è semplicemente la sua coordinata \(z\), che è 1.
Quindi, l'altezza \(h = 1\).
\[ V = \frac{1}{3} \cdot \text{Area}_{OAB} \cdot h = \frac{1}{3} \cdot \frac{1}{2} \cdot 1 = \frac{1}{6} \]Il **volume** del tetraedro è \(\frac{1}{6}\).
b) Calcolo dell'angolo in gradi che la faccia ABC forma con la base OAB
L'angolo fra la faccia \(ABC\) e la base \(OAB\) è uguale all'angolo di una sezione normale del diedro formato dai piani \(ABC\) e \(OAB\).
La linea di intersezione dei due piani è il segmento \(AB\).
Consideriamo il punto medio \(M\) di \(AB\). Le coordinate di \(M\) sono: \[ M = \left(\frac{1+0}{2}, \frac{0+1}{2}, \frac{0+0}{2}\right) = \left(\frac{1}{2}, \frac{1}{2}, 0\right) \]
Essendo il triangolo \(ABC\) equilatero e il triangolo \(OAB\) isoscele sulla base \(AB\), il punto medio \(M\) di \(AB\) è anche il piede dell'altezza di \(OAB\) uscente da \(O\) e di \(ABC\) uscente da \(C\).
Calcoliamo le lunghezze di queste altezze:
- **Altezza OM (di OAB):** Distanza di \(O(0,0,0)\) da \(M(\frac{1}{2}, \frac{1}{2}, 0)\). \[ OM = \sqrt{\left(\frac{1}{2}-0\right)^2 + \left(\frac{1}{2}-0\right)^2 + (0-0)^2} = \sqrt{\frac{1}{4} + \frac{1}{4}} = \sqrt{\frac{2}{4}} = \frac{\sqrt{2}}{2} \]
- **Altezza CM (di ABC):** Distanza di \(C(0,0,1)\) da \(M(\frac{1}{2}, \frac{1}{2}, 0)\). \[ CM = \sqrt{\left(\frac{1}{2}-0\right)^2 + \left(\frac{1}{2}-0\right)^2 + (0-1)^2} = \sqrt{\frac{1}{4} + \frac{1}{4} + 1} = \sqrt{\frac{1}{2} + 1} = \sqrt{\frac{3}{2}} = \frac{\sqrt{6}}{2} \]
L'angolo richiesto, \(\alpha\), è l'angolo formato dai segmenti \(OM\) e \(CM\), cioè \(\angle OMC\).
Consideriamo il triangolo \(OMC\). I suoi vertici sono \(O(0,0,0)\), \(M(\frac{1}{2}, \frac{1}{2}, 0)\) e \(C(0,0,1)\).
Osserviamo che il segmento \(OC\) (lungo 1) giace sull'asse \(z\), mentre il segmento \(OM\) giace sul piano \(xy\). Pertanto, il triangolo \(OMC\) è **rettangolo in O**.
Nel triangolo rettangolo \(OMC\), le lunghezze dei lati sono: * Cateto \(OM = \frac{\sqrt{2}}{2}\) * Cateto \(OC = 1\) * Ipotenusa \(CM = \frac{\sqrt{6}}{2}\)
L'angolo \(\alpha\) (che è \(\angle OMC\)) è l'angolo tra l'ipotenusa \(CM\) e il cateto adiacente \(OM\). Possiamo calcolarlo usando la funzione coseno:
\[ \cos \alpha = \frac{\text{lato adiacente}}{\text{ipotenusa}} = \frac{OM}{CM} \] \[ \cos \alpha = \frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{6}}{2}} = \frac{\sqrt{2}}{\sqrt{6}} = \sqrt{\frac{2}{6}} = \sqrt{\frac{1}{3}} = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3} \]Per trovare \(\alpha\) in gradi:
\[ \alpha = \arccos\left(\frac{\sqrt{3}}{3}\right) \] \[ \alpha \approx \arccos(0.57735) \approx 54.735^\circ \]L'angolo che la faccia \(ABC\) forma con la base \(OAB\) è di circa \(54.735\) gradi.