Soluzione quesito 1:

Per applicare il Teorema di Lagrange alla funzione \(f(x)\) nell'intervallo \([0, 2]\), devono essere soddisfatte due condizioni:

1. La funzione deve essere continua nell'intervallo chiuso \([0, 2]\).
2. La funzione deve essere derivabile nell'intervallo aperto \((0, 2)\).

1. Continuità in \(x=1\)

La funzione è definita a tratti, quindi dobbiamo assicurarci la continuità nel punto di raccordo \(x=1\). Dobbiamo avere:

\[ \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = f(1) \]

Calcoliamo i limiti:

• \(\lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} x^3 = 1^3 = 1\)
• \(\lim_{x \to 1^+} f(x) = \lim_{x \to 1^+} (x^2 - kx + k) = 1^2 - k(1) + k = 1 - k + k = 1\)
• \(f(1) = 1^3 = 1\)

Poiché i limiti e il valore della funzione in \(x=1\) sono tutti uguali a 1, la funzione è continua in \(x=1\) **per qualsiasi valore di \(k\)**. Quindi, la condizione di continuità è sempre soddisfatta.

2. Derivabilità in \(x=1\)

Dobbiamo calcolare le derivate dei singoli rami:

• Per \(0 \le x < 1\), \(f'(x) = \frac{d}{dx}(x^3) = 3x^2\)
• Per \(1 < x \le 2\), \(f'(x) = \frac{d}{dx}(x^2 - kx + k) = 2x - k\)

Per la derivabilità in \(x=1\), le derivate sinistra e destra devono essere uguali:

\[ \lim_{x \to 1^-} f'(x) = \lim_{x \to 1^+} f'(x) \] \[ \lim_{x \to 1^-} (3x^2) = \lim_{x \to 1^+} (2x - k) \] \[ 3(1)^2 = 2(1) - k \] \[ 3 = 2 - k \] \[ k = 2 - 3 \] \[ k = -1 \]

Quindi, la funzione è derivabile in \(x=1\) solo se \(k = -1\).

Per \(k = -1\), la funzione diventa:

\[ f(x) = \begin{cases} x^3 & \text{se } 0 \le x \le 1 \\ x^2 + x - 1 & \text{se } 1 < x \le 2 \end{cases} \]

Con \(k = -1\), le condizioni del Teorema di Lagrange sono soddisfatte.

Trovare il punto \(c\)

Il Teorema di Lagrange afferma che esiste almeno un punto \(c \in (0, 2)\) tale che:

\[ f'(c) = \frac{f(2) - f(0)}{2 - 0} \]

Calcoliamo \(f(0)\) e \(f(2)\):

• \(f(0) = 0^3 = 0\)
• \(f(2) = 2^2 + 2 - 1 = 4 + 2 - 1 = 5\) (usando \(k=-1\))

Quindi:

\[ \frac{f(2) - f(0)}{2 - 0} = \frac{5 - 0}{2} = \frac{5}{2} \]

Ora dobbiamo trovare \(c\) tale che \(f'(c) = \frac{5}{2}\). Abbiamo due casi per \(f'(x)\):

Caso 1: \(0 < c \le 1\) (usando \(f'(x) = 3x^2\))

\[ 3c^2 = \frac{5}{2} \] \[ c^2 = \frac{5}{6} \] \[ c = \sqrt{\frac{5}{6}} \quad (\text{scartiamo la soluzione negativa poiché } c \in (0, 2)) \]

Verifichiamo se \(c = \sqrt{\frac{5}{6}}\) è nell'intervallo \((0, 1]\):

\(\sqrt{\frac{5}{6}} \approx \sqrt{0.833} \approx 0.913\). Questo valore è compreso tra 0 e 1, quindi è una soluzione valida.

Caso 2: \(1 < c < 2\) (usando \(f'(x) = 2x - k = 2x + 1\), dato che \(k=-1\))

\[ 2c + 1 = \frac{5}{2} \] \[ 2c = \frac{5}{2} - 1 \] \[ 2c = \frac{3}{2} \] \[ c = \frac{3}{4} \]

Verifichiamo se \(c = \frac{3}{4}\) è nell'intervallo \((1, 2)\):

\(\frac{3}{4} = 0.75\). Questo valore non è maggiore di 1, quindi **non** è una soluzione valida per questo caso.

Conclusione:

• Il parametro \(k\) per cui il Teorema di Lagrange è applicabile è \(k = -1\).
• Il punto \(c\) garantito dal teorema è \(c = \sqrt{\frac{5}{6}}\).

Soluzione quesito 2:

Il Teorema della media integrale afferma che, se una funzione \( f(x) \) è continua su un intervallo \( [a, b] \), allora esiste un punto \( c \in [a, b] \) tale che:

\[ f(c) = \frac{1}{b-a} \int_a^b f(x) \, dx \]

Il valore \(\frac{1}{b-a} \int_a^b f(x) \, dx\) è il valore medio della funzione nell'intervallo.

Nel nostro caso, \( f(x) = \ln(x) \), l'intervallo è \( [1, e^2] \), quindi \( a=1 \) e \( b=e^2 \).

1. Calcolo del valore medio

Dobbiamo calcolare l'integrale definito \( \int_1^{e^2} \ln(x) \, dx \). Usiamo l'integrazione per parti, ricordando che \( \int \ln(x) \, dx = x \ln(x) - x + C \).

\[ \int_1^{e^2} \ln(x) \, dx = [x \ln(x) - x]_1^{e^2} \]

Applichiamo il Teorema Fondamentale del Calcolo Integrale:

\[ = (e^2 \ln(e^2) - e^2) - (1 \ln(1) - 1) \]

Sappiamo che \( \ln(e^2) = 2 \) e \( \ln(1) = 0 \):

\[ = (2e^2 - e^2) - (-1) \] \[ = e^2 + 1 \]

Ora calcoliamo il valore medio \( \bar{f} \):

\[ \bar{f} = \frac{1}{b-a} \int_a^b f(x) \, dx = \frac{1}{e^2 - 1} (e^2 + 1) = \frac{e^2 + 1}{e^2 - 1} \]

Il valore medio della funzione è \( \frac{e^2 + 1}{e^2 - 1} \).

2. Trovare il punto \(c\)

Dobbiamo trovare un punto \( c \in [1, e^2] \) tale che \( f(c) = \bar{f} \), ovvero:

\[ \ln(c) = \frac{e^2 + 1}{e^2 - 1} \]

Per trovare \( c \), esponenziamo entrambi i lati:

\[ c = e^{\frac{e^2 + 1}{e^2 - 1}} \]

Verifichiamo che questo valore di \( c \) sia nell'intervallo \( [1, e^2] \).

Consideriamo l'esponente: \( \frac{e^2 + 1}{e^2 - 1} \).

Sappiamo che \( e \approx 2.718 \), quindi \( e^2 \approx 7.389 \).

\[ \frac{e^2 + 1}{e^2 - 1} \approx \frac{7.389 + 1}{7.389 - 1} = \frac{8.389}{6.389} \approx 1.313 \]

Quindi, \( c \approx e^{1.313} \).

Dato che \( e^1 = e \approx 2.718 \) ed \( e^2 \approx 7.389 \), e \( 1 < 1.313 < 2 \), allora \( e^1 < e^{1.313} < e^2 \).

Quindi \( c = e^{\frac{e^2 + 1}{e^2 - 1}} \) è effettivamente compreso nell'intervallo \( [1, e^2] \).

Conclusione:

• Il valore medio della funzione \(f(x) = \ln(x)\) nell'intervallo \( [1, e^2] \) è \( \frac{e^2 + 1}{e^2 - 1} \).
• Il punto \(c\) che soddisfa la tesi del Teorema della media è \( c = e^{\frac{e^2 + 1}{e^2 - 1}} \).

Soluzione quesito 6:

Consideriamo la funzione \( f(x) = \ln(x-5) + x - 7 \).

1. Applicazione del Teorema degli Zeri

Il Teorema degli Zeri (o Teorema di Bolzano) afferma che se una funzione \(f(x)\) è continua in un intervallo chiuso \([a, b]\) e \(f(a)\) e \(f(b)\) hanno segni opposti (cioè \(f(a) \cdot f(b) < 0\)), allora esiste almeno un punto \(c \in (a, b)\) tale che \(f(c) = 0\).

Nel nostro caso, l'intervallo è \([6, 7]\).

Condizione di Continuità:

La funzione \(f(x) = \ln(x-5) + x - 7\) è continua per \(x-5 > 0\), ovvero per \(x > 5\). Poiché l'intervallo \([6, 7]\) è contenuto nel dominio \( (5, +\infty) \), la funzione è continua in \([6, 7]\).

Valutazione agli estremi dell'intervallo:

Calcoliamo il valore della funzione agli estremi dell'intervallo:

\[ f(6) = \ln(6-5) + 6 - 7 = \ln(1) - 1 = 0 - 1 = -1 \] \[ f(7) = \ln(7-5) + 7 - 7 = \ln(2) + 0 = \ln(2) \approx 0.693 \]

Poiché \(f(6) = -1 < 0\) e \(f(7) = \ln(2) > 0\), i valori di \(f(x)\) agli estremi dell'intervallo hanno segni opposti. Pertanto, per il Teorema degli Zeri, esiste almeno una soluzione dell'equazione \(f(x) = 0\) nell'intervallo \((6, 7)\).

2. Unicità della soluzione (Metodo 1 - Monotonia)

Per dimostrare l'unicità della soluzione, possiamo studiare la monotonia della funzione, calcolando la sua derivata prima.

\[ f'(x) = \frac{d}{dx}(\ln(x-5) + x - 7) \] \[ f'(x) = \frac{1}{x-5} + 1 \]

Nel dominio della funzione (\(x > 5\)), abbiamo \(x-5 > 0\), quindi \(\frac{1}{x-5} > 0\). Di conseguenza, \(f'(x) = \frac{1}{x-5} + 1 > 0\) per ogni \(x > 5\).

Dato che \(f'(x) > 0\) nell'intervallo \((6, 7)\), la funzione \(f(x)\) è strettamente crescente in tale intervallo. Una funzione strettamente monotona (crescente o decrescente) può attraversare l'asse delle ascisse al massimo una volta. Poiché abbiamo già dimostrato l'esistenza di uno zero, questo zero deve essere unico.

Unicità della soluzione (Metodo 2 - Analisi Grafica)

Per stabilire l'unicità della soluzione, possiamo riscrivere l'equazione \( \ln(x-5) + x - 7 = 0 \) come \( \ln(x-5) = -x + 7 \). Rappresentiamo nello stesso piano cartesiano le due funzioni:

• \( a(x) = \ln(x-5) \) (una funzione logaritmica traslata)
• \( b(x) = -x + 7 \) (una retta con pendenza negativa)

Il punto di intersezione tra queste due curve corrisponde alla soluzione dell'equazione originale.

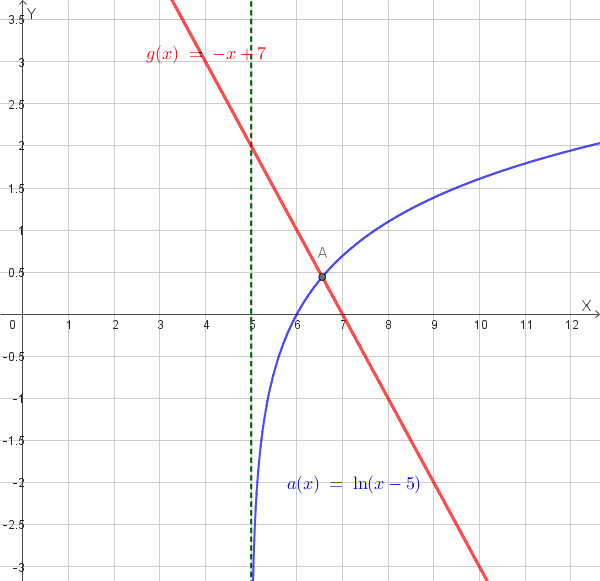
Come si vede dal grafico le due curve si intersecano una sola volta, in un punto con ascissa fra 6 e 7. Quindi in \((6, 7)\) l'equazione ha una sola soluzione.

3. Calcolo di un valore approssimato (Metodo di Bisezione)

Vogliamo trovare una soluzione approssimata a meno di un decimo. Partiamo dall'intervallo \([a_0, b_0] = [6, 7]\).

• \(f(6) = -1\)
• \(f(7) = \ln(2) \approx 0.693\)

Iterazione 1:

Punto medio \(m_1 = \frac{6+7}{2} = 6.5\)

\[ f(6.5) = \ln(6.5-5) + 6.5 - 7 = \ln(1.5) - 0.5 \approx 0.405 - 0.5 = -0.095 \]

Poiché \(f(6.5) < 0\) e \(f(7) > 0\), la radice si trova nell'intervallo \([6.5, 7]\).

Ampiezza dell'intervallo: \(7 - 6.5 = 0.5\).

Iterazione 2:

Punto medio \(m_2 = \frac{6.5+7}{2} = 6.75\)

\[ f(6.75) = \ln(6.75-5) + 6.75 - 7 = \ln(1.75) - 0.25 \approx 0.560 - 0.25 = 0.310 \]

Poiché \(f(6.5) < 0\) e \(f(6.75) > 0\), la radice si trova nell'intervallo \([6.5, 6.75]\).

Ampiezza dell'intervallo: \(6.75 - 6.5 = 0.25\).

Iterazione 3:

Punto medio \(m_3 = \frac{6.5+6.75}{2} = 6.625\)

\[ f(6.625) = \ln(6.625-5) + 6.625 - 7 = \ln(1.625) - 0.375 \approx 0.485 - 0.375 = 0.110 \]

Poiché \(f(6.5) < 0\) e \(f(6.625) > 0\), la radice si trova nell'intervallo \([6.5, 6.625]\).

Ampiezza dell'intervallo: \(6.625 - 6.5 = 0.125\).

Iterazione 4:

Punto medio \(m_4 = \frac{6.5+6.625}{2} = 6.5625\)

\[ f(6.5625) = \ln(6.5625-5) + 6.5625 - 7 = \ln(1.5625) - 0.4375 \approx 0.446 - 0.4375 = 0.0085 \]

Poiché \(f(6.5) < 0\) e \(f(6.5625) > 0\), la radice si trova nell'intervallo \([6.5, 6.5625]\).

Ampiezza dell'intervallo: \(6.5625 - 6.5 = 0.0625\).

L'ampiezza dell'intervallo (\(0.0625\)) è minore di un decimo (\(0.1\)). Possiamo prendere come valore approssimato uno degli estremi o il punto medio dell'ultimo intervallo.

Un valore approssimato a meno di un decimo può essere \(x \approx 6.5\).

4. Calcolo di un valore approssimato (Metodo delle Tangenti / Newton-Raphson)

Il metodo di Newton-Raphson (o delle tangenti) si basa sulla formula iterativa:

\[ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \]

Abbiamo \(f(x) = \ln(x-5) + x - 7\) e \(f'(x) = \frac{1}{x-5} + 1\).

Scegliamo un punto iniziale \(x_0\) nell'intervallo \([6, 7]\). Un buon punto di partenza è quello dove la funzione cambia segno, ad esempio \(x_0 = 6.5\).

Iterazione 1:

\(x_0 = 6.5\)

\[ f(6.5) = \ln(1.5) - 0.5 \approx -0.095 \] \[ f'(6.5) = \frac{1}{6.5-5} + 1 = \frac{1}{1.5} + 1 = \frac{2}{3} + 1 = \frac{5}{3} \approx 1.667 \] \[ x_1 = x_0 - \frac{f(x_0)}{f'(x_0)} = 6.5 - \frac{-0.095}{1.667} = 6.5 + 0.057 = 6.557 \]

Iterazione 2:

\(x_1 = 6.557\)

\[ f(6.557) = \ln(6.557-5) + 6.557 - 7 = \ln(1.557) - 0.443 \approx 0.4427 - 0.443 = -0.0003 \] \[ f'(6.557) = \frac{1}{6.557-5} + 1 = \frac{1}{1.557} + 1 \approx 0.642 + 1 = 1.642 \] \[ x_2 = x_1 - \frac{f(x_1)}{f'(x_1)} = 6.557 - \frac{-0.0003}{1.642} = 6.557 + 0.00018 = 6.55718 \]

Il valore approssimato è \(x \approx 6.56\). Questo è già molto vicino e soddisfa ampiamente la richiesta di approssimazione a meno di un decimo.

Entrambi i metodi indicano che la soluzione è approssimativamente \(6.6\) (arrotondando \(6.56\) a un decimo).

Conclusione:

• Mediante il Teorema degli Zeri, è stato dimostrato che l'equazione ammette almeno una soluzione nell'intervallo \((6, 7)\).
• Studiando la derivata prima e con l'analisi grafica, è stato dimostrato che la soluzione è unica.
• Utilizzando il metodo di bisezione e il metodo delle tangenti, un valore approssimato della soluzione a meno di un decimo è \(x \approx 6.6\).

Soluzione quesito 7:

Due rette nello spazio si dicono sghembe se non sono parallele e non si intersecano.

1. Determinare i vettori direttori delle rette

Per la retta \(r\):

Il vettore direttore \(\vec{v}_r\) si ricava direttamente dai coefficienti di \(t\) nelle equazioni parametriche:

\[ \vec{v}_r = (1, -1, 2) \]

Un punto sulla retta \(r\) è \(P_r = (1, 2, 3)\) (ponendo \(t=0\)).

Per la retta \(s\):

Possiamo trovare il vettore direttore della retta \(s\) trovando prima la sua forma parametrica dal sistema di equazioni:

\[ \begin{cases} x - y + z = 0 \\ 2x + y - z = 1 \end{cases} \]

Sommando le due equazioni per eliminare \(y\) e \(z\):

\[ (x - y + z) + (2x + y - z) = 0 + 1 \Rightarrow 3x = 1 \Rightarrow x = \frac{1}{3} \]

Ora, poniamo \(z=k\). Sostituendo \(x = \frac{1}{3}\) e \(z=k\) nella prima equazione:

\[ \frac{1}{3} - y + k = 0 \Rightarrow y = \frac{1}{3} + k \]

Quindi la forma parametrica della retta \(s\) è:

\[ \begin{cases} x = \frac{1}{3} \\ y = \frac{1}{3} + k \\ z = k \end{cases} \]

Da questa forma parametrica, un punto sulla retta \(s\) è \(P_s = \left(\frac{1}{3}, \frac{1}{3}, 0\right)\) (ponendo \(k=0\)), e il suo vettore direttore \(\vec{v}_s\) è \((0, 1, 1)\).

2. Verificare se le rette sono parallele

Le rette sono parallele se i loro vettori direttori sono proporzionali.

\(\vec{v}_r = (1, -1, 2)\) e \(\vec{v}_s = (0, 1, 1)\).

Non esiste una costante \(k\) tale che \(\vec{v}_r = k \vec{v}_s\), poiché il primo componente di \(\vec{v}_s\) è 0 mentre quello di \(\vec{v}_r\) è 1. Questo dimostra che le rette NON sono parallele.

3. Verificare se le rette si intersecano

Per verificare se le rette si intersecano, sostituiamo le equazioni parametriche della retta \(r\) nelle equazioni cartesiane della retta \(s\).

Equazioni parametriche di \(r\): \(x = 1 + t, y = 2 - t, z = 3 + 2t\)

Equazioni di \(s\):

\[ \begin{cases} x - y + z = 0 \\ 2x + y - z = 1 \end{cases} \]

Sostituendo le espressioni di \(x, y, z\) in funzione di \(t\):

\[ \begin{cases} (1 + t) - (2 - t) + (3 + 2t) = 0 \\ 2(1 + t) + (2 - t) - (3 + 2t) = 1 \end{cases} \]

Semplifichiamo le equazioni:

Prima equazione:

\[ 1 + t - 2 + t + 3 + 2t = 0 \Rightarrow 4t + 2 = 0 \Rightarrow 4t = -2 \Rightarrow t = -\frac{1}{2} \]

Seconda equazione:

\[ 2 + 2t + 2 - t - 3 - 2t = 1 \Rightarrow -t + 1 = 1 \Rightarrow -t = 0 \Rightarrow t = 0 \]

Abbiamo ottenuto due valori diversi per \(t\) (cioè \(t = -\frac{1}{2}\) dalla prima equazione e \(t = 0\) dalla seconda). Questo significa che non esiste un valore di \(t\) che soddisfi contemporaneamente entrambe le equazioni, e quindi le rette NON si intersecano.

Conclusione

Poiché le rette \(r\) ed \(s\) non sono parallele e non si intersecano, esse sono sghembe.

Soluzione quesito 8:

Siano \(a\) e \(b\) le dimensioni del foglio rettangolare originale.

Assumiamo, senza perdita di generalità, che \(a\) sia il lato più lungo e \(b\) il lato più corto, quindi \(a \ge b\).

1. Condizione sull'area:

L'area del foglio è 1 m². Quindi:

\[ a \cdot b = 1 \quad (*) \]

2. Taglio del foglio e nuove dimensioni:

Il foglio viene tagliato a metà parallelamente al lato minore (\(b\)). Questo significa che il lato \(a\) viene diviso in due, ottenendo due rettangoli più piccoli.

Detto ABCD il rettangolo, tracciamo la retta per il punto medio E di AB (lato di lunghezza \(a\)) parallela al lato minore BC (lato di lunghezza \(b\)).

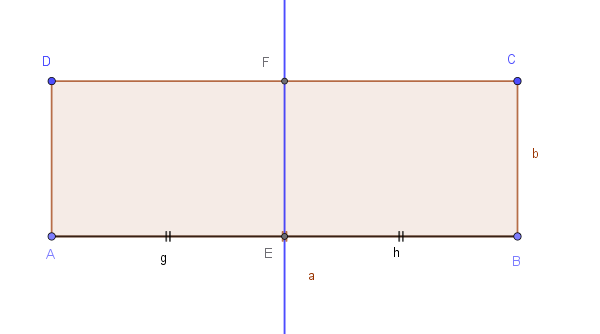
Le dimensioni di ciascuno dei due nuovi rettangoli saranno \(a/2\) e \(b\).

3. Condizione di similitudine:

I due nuovi rettangoli devono essere simili al rettangolo di partenza. Affinché due rettangoli siano simili, il rapporto tra il lato più lungo e il lato più corto deve essere lo stesso.

• Rapporto del rettangolo originale: Poiché \(a \ge b\), il rapporto tra il lato lungo e il lato corto del rettangolo originale è \( \frac{a}{b} \).
• Rapporto del nuovo rettangolo:

  I lati del nuovo rettangolo sono \(a/2\) e \(b\). Dobbiamo confrontare queste due lunghezze per stabilire quale sia il lato più lungo e quale il più corto nel nuovo rettangolo.

  Sia \(k = \frac{a}{b}\) il rapporto tra i lati del rettangolo originale. Dalla condizione \(a \ge b\), segue \(k \ge 1\).

  Le dimensioni del nuovo rettangolo sono \( \frac{a}{2} = \frac{kb}{2} \) e \( b \).

  Consideriamo i possibili casi per la relazione tra \( \frac{a}{2} \) e \( b \):

  Caso 1: \( b \ge \frac{a}{2} \) (ovvero \( b \) è il lato più lungo del nuovo rettangolo)

  Questa condizione implica \( b \ge \frac{kb}{2} \), che semplifica a \( 1 \ge \frac{k}{2} \), ovvero \( k \le 2 \).

  Il rapporto tra il lato più lungo e il lato più corto del nuovo rettangolo è \( \frac{b}{a/2} = \frac{b}{kb/2} = \frac{2}{k} \).

  Per la similitudine, questo rapporto deve essere uguale al rapporto del rettangolo originale:

  \[ k = \frac{2}{k} \Rightarrow k^2 = 2 \Rightarrow k = \sqrt{2} \]

  Verifichiamo la consistenza: \( k = \sqrt{2} \approx 1.414 \). Poiché \( \sqrt{2} \le 2 \), questo caso è consistente.

  Caso 2: \( \frac{a}{2} > b \) (ovvero \( \frac{a}{2} \) è il lato più lungo del nuovo rettangolo)

  Questa condizione implica \( \frac{a}{2} > b \), ovvero \( \frac{kb}{2} > b \), che semplifica a \( \frac{k}{2} > 1 \), ovvero \( k > 2 \).

  Il rapporto tra il lato più lungo e il lato più corto del nuovo rettangolo è \( \frac{a/2}{b} = \frac{kb/2}{b} = \frac{k}{2} \).

  Per la similitudine, questo rapporto deve essere uguale al rapporto del rettangolo originale:

  \[ k = \frac{k}{2} \]

  Questa equazione implica \( 1 = \frac{1}{2} \), che è un'affermazione falsa. Pertanto, questo caso non è possibile.

  Caso 3: \( \frac{a}{2} = b \) (ovvero i lati del nuovo rettangolo sono uguali, è un quadrato)

  Se \( a/2 = b \), i due rettangoli ottenuti sono quadrati. Un quadrato ha un rapporto tra i lati di 1. Il rettangolo originale ABCD, invece, non è un quadrato (poiché \(a > b\), ovvero \(a \ne b\)). Pertanto, i due nuovi rettangoli non possono essere simili al rettangolo ABCD.

  L'unico caso consistente è \( k = \sqrt{2} \).

  Quindi, il rapporto tra i lati del rettangolo è \( \frac{a}{b} = \sqrt{2} \). Questo significa che \( a = \sqrt{2}b \quad (**) \).

  Questo rapporto, circa 1.414, è la caratteristica fondamentale dei formati carta della serie ISO 216 (come l'A4), che permette di mantenere la proporzione tagliando o raddoppiando il foglio.

  Le dimensioni del formato A4 in cm sono di 21,0 cm x 29,7 cm e difatti: \( 21.0 \cdot \sqrt{2} \approx 29.7 \)

4. Calcolo delle misure di \(a\) e \(b\):

Ora abbiamo un sistema di due equazioni con due incognite:

\[ \begin{cases} a \cdot b = 1 \\ a = \sqrt{2}b \end{cases} \]

Sostituiamo la seconda equazione nella prima:

\[ (\sqrt{2}b) \cdot b = 1 \] \[ \sqrt{2}b^2 = 1 \] \[ b^2 = \frac{1}{\sqrt{2}} \]

Prendendo la radice quadrata (solo il valore positivo, essendo una lunghezza):

\[ b = \sqrt{\frac{1}{\sqrt{2}}} = \frac{1}{\sqrt[4]{2}} = 2^{-1/4} \text{ m} \]

Ora troviamo \(a\) usando la relazione \(a = \sqrt{2}b\):

\[ a = \sqrt{2} \cdot \frac{1}{\sqrt[4]{2}} = 2^{1/2} \cdot 2^{-1/4} = 2^{1/2 - 1/4} = 2^{1/4} \text{ m} \]

Valori approssimati:

\[ a = 2^{1/4} \approx 1.189 \text{ m} \] \[ b = 2^{-1/4} \approx 0.841 \text{ m} \]

Conclusione:

Le misure del foglio rettangolare sono \(a = 2^{1/4}\) metri (il lato più lungo) e \(b = 2^{-1/4}\) metri (il lato più corto). Il rapporto tra i lati è \( \sqrt{2} \).