Questionario sulla Concavità di una Funzione. Studio dei flessi
Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.


Risolvi da solo i singoli quesiti e controlla la soluzione premendo il tasto corrispondente.
Studia la concavità della seguente funzione e determina gli eventuali flessi:
\[f(x) = x^3 - 6x^2 + 9x + 2\]Soluzione quesito 1:
Premessa importante:
Una funzione cubica (polinomio di terzo grado) del tipo \(f(x) = ax^3 + bx^2 + cx + d\) con \(a \neq 0\) ammette sempre uno ed un solo flesso, che è anche centro di simmetria per il grafico della funzione.
Perché? La derivata seconda di una cubica è \(f''(x) = 6ax + 2b\), che è una funzione lineare. Una retta si annulla in un unico punto e cambia segno passando per quel punto. Quindi la concavità cambia esattamente una volta, determinando un unico punto di flesso.
Passo 1: Dominio
La funzione è polinomiale, quindi il dominio è:
\[D = \mathbb{R}\]Passo 2: Calcolo della derivata prima
\[f'(x) = 3x^2 - 12x + 9\]Passo 3: Calcolo della derivata seconda
\[f''(x) = 6x - 12 = 6(x - 2)\]Passo 4: Studio del segno di \(f''(x)\)
Risolviamo \(f''(x) = 0\):
\[6(x - 2) = 0 \implies x = 2\]| Intervallo | \(f''(x)\) | Concavità |
|---|---|---|
| \(x < 2\) | − | Concava verso il basso (∩) |
| \(x > 2\) | + | Concava verso l'alto (∪) |
Passo 5: Determinazione del flesso
Poiché la derivata seconda cambia segno in \(x = 2\), questo è un punto di flesso.
Calcoliamo le coordinate del punto di flesso:
\[f(2) = 2^3 - 6(2)^2 + 9(2) + 2 = 8 - 24 + 18 + 2 = 4\]Verifica che il flesso è centro di simmetria:
Un punto \(C(a, b)\) è centro di simmetria per una funzione \(f\) se la funzione trasformata tramite simmetria centrale rispetto a \(C\) coincide con \(f\) stessa.
Le equazioni della simmetria centrale rispetto al punto generico \((a, b)\) sono:
\[\begin{cases} x' = 2a - x \\ y' = 2b - y \end{cases}\]Sostituiamo le coordinate del flesso \(F(2, 4)\):
\[\begin{cases} x' = 4 - x \\ y' = 8 - y \end{cases}\]Ricaviamo \(x\) e \(y\) in funzione di \(x'\) e \(y'\):
\[\begin{cases} x = 4 - x' \\ y = 8 - y' \end{cases}\]Sostituiamo nella funzione originale \(y = f(x) = x^3 - 6x^2 + 9x + 2\):
\[8 - y' = (4-x')^3 - 6(4-x')^2 + 9(4-x') + 2\]Sviluppiamo il secondo membro:
\[(4-x')^3 = 64 - 48x' + 12x'^2 - x'^3\] \[6(4-x')^2 = 6(16 - 8x' + x'^2) = 96 - 48x' + 6x'^2\] \[9(4-x') = 36 - 9x'\]Quindi:
\[8 - y' = 64 - 48x' + 12x'^2 - x'^3 - 96 + 48x' - 6x'^2 + 36 - 9x' + 2\] \[8 - y' = -x'^3 + 6x'^2 - 9x' + 6\] \[- y' = -x'^3 + 6x'^2 - 9x' - 2\] \[y' = x'^3 - 6x'^2 + 9x' + 2\]La funzione trasformata è \(y' = x'^3 - 6x'^2 + 9x' + 2 = f(x')\), che coincide esattamente con la funzione originale.
Conclusione: Il punto \(F(2, 4)\) è effettivamente centro di simmetria del grafico. ✓
Conclusioni:
Il grafico della funzione è di questo tipo:

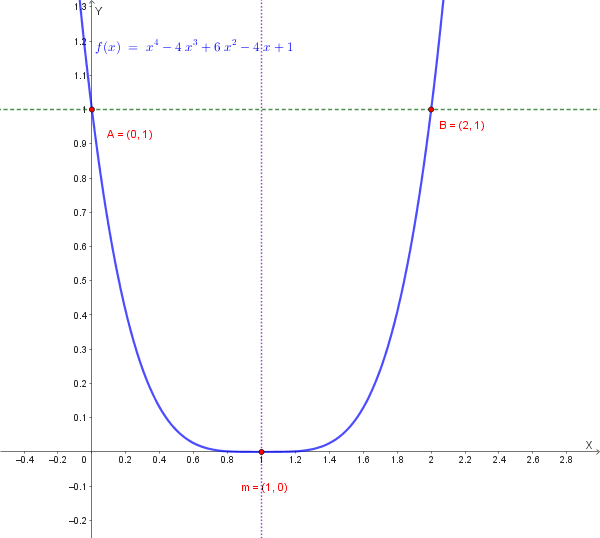
Studia la concavità della seguente funzione e determina gli eventuali flessi:
\[f(x) = x^4 - 4x^3 + 6x^2 - 4x + 1\]Inoltre:
Soluzione quesito 2:
Premessa importante:
Una funzione quartica (polinomio di quarto grado) del tipo \(f(x) = ax^4 + bx^3 + cx^2 + dx + e\) con \(a \neq 0\) può avere 0, 1 o 2 flessi.
Perché? La derivata seconda di una quartica è \(f''(x) = 12ax^2 + 6bx + 2c\), che è una parabola. Una parabola può non avere zeri reali (nessun flesso), avere uno zero doppio (un flesso) oppure due zeri distinti (due flessi).
Passo 1: Dominio
La funzione è polinomiale, quindi il dominio è:
\[D = \mathbb{R}\]Passo 2: Calcolo della derivata prima
\[f'(x) = 4x^3 - 12x^2 + 12x - 4\]Passo 3: Calcolo della derivata seconda
\[f''(x) = 12x^2 - 24x + 12 = 12(x^2 - 2x + 1) = 12(x-1)^2\]Passo 4: Studio del segno di \(f''(x)\)
Risolviamo \(f''(x) = 0\):
\[12(x - 1)^2 = 0 \implies x = 1\]Poiché \(f''(x) = 12(x-1)^2 \geq 0\) per ogni \(x \in \mathbb{R}\) e si annulla solo in \(x = 1\) con molteplicità 2, la derivata seconda non cambia segno.
| Intervallo | \(f''(x)\) | Concavità |
|---|---|---|
| \(x < 1\) | + | Concava verso l'alto (∪) |
| \(x = 1\) | 0 | - |
| \(x > 1\) | + | Concava verso l'alto (∪) |
Passo 5: Determinazione dei flessi
Poiché la derivata seconda non cambia segno in \(x = 1\) (si annulla ma rimane sempre positiva), il punto \(x = 1\) non è un flesso.
Calcoliamo comunque il valore della funzione in \(x = 1\):
\[f(1) = 1 - 4 + 6 - 4 + 1 = 0\]Il punto \((1, 0)\) è un punto in cui la concavità ha un "appiattimento" ma non cambia verso.
Conclusioni:
Osservazione:
Notiamo che \(f(x) = (x-1)^4\), infatti:
\[(x-1)^4 = x^4 - 4x^3 + 6x^2 - 4x + 1\]Questa è la funzione potenza quarta traslata, che ha un minimo assoluto in \(x = 1\) e nessun flesso.
a) Dimostrazione della simmetria rispetto alla retta \(x = 1\)
Un grafico è simmetrico rispetto alla retta verticale \(x = a\) se la funzione trasformata tramite simmetria assiale rispetto a tale retta coincide con la funzione originale.
Le equazioni della simmetria assiale rispetto alla retta verticale \(x = a\) sono:
\[\begin{cases} x' = 2a - x \\ y' = y \end{cases}\]Sostituiamo \(a = 1\):
\[\begin{cases} x' = 2 - x \\ y' = y \end{cases}\]Ricaviamo \(x\) e \(y\) in funzione di \(x'\) e \(y'\):
\[\begin{cases} x = 2 - x' \\ y = y' \end{cases}\]Sostituiamo nella funzione originale \(y = f(x) = x^4 - 4x^3 + 6x^2 - 4x + 1\):
\[y' = (2-x')^4 - 4(2-x')^3 + 6(2-x')^2 - 4(2-x') + 1\]Sviluppiamo i singoli termini:
\[(2-x')^4 = 16 - 32x' + 24x'^2 - 8x'^3 + x'^4\] \[4(2-x')^3 = 4(8 - 12x' + 6x'^2 - x'^3) = 32 - 48x' + 24x'^2 - 4x'^3\] \[6(2-x')^2 = 6(4 - 4x' + x'^2) = 24 - 24x' + 6x'^2\] \[4(2-x') = 8 - 4x'\]Sostituendo:
\[y' = 16 - 32x' + 24x'^2 - 8x'^3 + x'^4 - 32 + 48x' - 24x'^2 + 4x'^3 + 24 - 24x' + 6x'^2 - 8 + 4x' + 1\]Semplificando termine per termine:
Quindi:
\[y' = x'^4 - 4x'^3 + 6x'^2 - 4x' + 1\]La funzione trasformata coincide esattamente con la funzione originale \(f(x')\).
Conclusione: Il grafico di \(f\) è simmetrico rispetto alla retta \(x = 1\). ✓
b) Intervalli in cui \(f(x) > 1\)
Risolviamo la disequazione \(f(x) > 1\):
\[(x-1)^4 > 1\]Estraiamo la radice quarta (che mantiene il verso della disequazione essendo una funzione crescente):
\[|x-1| > 1\]Questa disequazione in valore assoluto equivale a:
\[x - 1 < -1 \quad \text{oppure} \quad x - 1 > 1\] \[x < 0 \quad \text{oppure} \quad x > 2\]Risposta: \(f(x) > 1\) per \(x \in (-\infty, 0) \cup (2, +\infty)\)
Verifica:
Il grafico della funzione è di questo tipo:
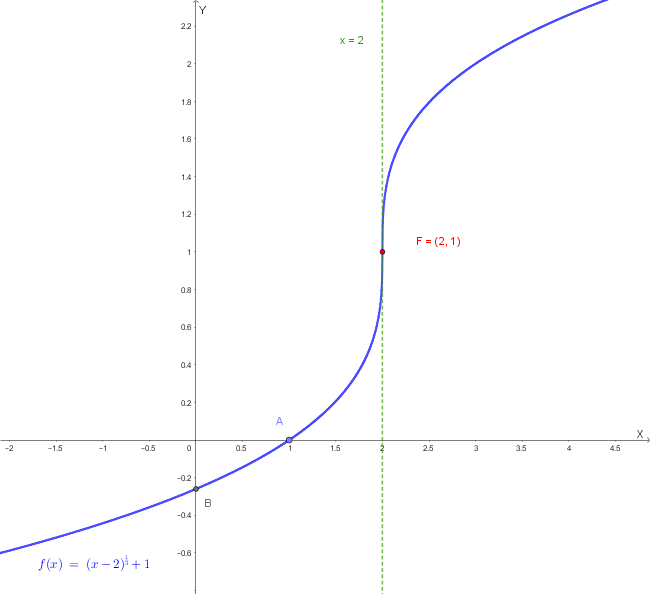
Studiare la concavità della seguente funzione irrazionale e determinare gli eventuali flessi:
\[f(x) = \sqrt[3]{x-2} + 1 \]Soluzione quesito 3:
Premessa importante:
Le funzioni irrazionali possono presentare punti di flesso anche dove la derivata seconda non esiste. In particolare, punti dove \(f''(x)\) non è definita ma la concavità cambia sono detti flessi a tangente verticale.
Passo 1: Dominio
La funzione \(f(x) = \sqrt[3]{x-2} + 1\) è definita per ogni \(x \in \mathbb{R}\) perché la radice cubica è definita per tutti i numeri reali.
\[D = \mathbb{R}\]Passo 2: Calcolo della derivata prima
Usando la regola della catena:
\[f'(x) = \frac{1}{3}(x-2)^{-2/3} \cdot 1 = \frac{1}{3(x-2)^{2/3}} = \frac{1}{3\sqrt[3]{(x-2)^2}}\]Osservazione: La derivata prima non esiste in \(x = 2\) (si annulla il denominatore).
Studio del segno di \(f'(x)\):
Poiché \((x-2)^{2/3} = [\sqrt[3]{x-2}]^2 > 0\) per ogni \(x \neq 2\), abbiamo:
\[f'(x) = \frac{1}{3(x-2)^{2/3}} > 0 \quad \text{per ogni } x \neq 2\]La funzione è sempre crescente in \(\mathbb{R} \setminus \{2\}\).
Analisi della tangente in \(x = 2\):
Passo 3: Calcolo della derivata seconda
Derivando \(f'(x) = \frac{1}{3}(x-2)^{-2/3}\):
\[f''(x) = \frac{1}{3} \cdot \left(-\frac{2}{3}\right)(x-2)^{-5/3} = -\frac{2}{9}(x-2)^{-5/3} = -\frac{2}{9(x-2)^{5/3}}\]Possiamo anche scrivere:
\[f''(x) = -\frac{2}{9\sqrt[3]{(x-2)^5}}\]Osservazione: La derivata seconda non esiste in \(x = 2\).
Passo 4: Studio del segno di \(f''(x)\)
Dobbiamo studiare il segno di \(f''(x) = -\frac{2}{9(x-2)^{5/3}}\).
Il segno dipende dal denominatore \((x-2)^{5/3}\):
| Intervallo | \(f''(x)\) | Concavità |
|---|---|---|
| \(x < 2\) | + | Concava verso l'alto (∪) |
| \(x = 2\) | non definita | - |
| \(x > 2\) | − | Concava verso il basso (∩) |
Passo 5: Determinazione dei flessi
La derivata seconda cambia segno in \(x = 2\):
Calcoliamo le coordinate del punto:
\[f(2) = \sqrt[3]{2-2} + 1 = \sqrt[3]{0} + 1 = 0 + 1 = 1\]Conclusione: Il punto \(F(2, 1)\) è un flesso a tangente verticale.
Verifica grafica del flesso:
Per verificare che \(F(2, 1)\) sia effettivamente un flesso, osserviamo che:
Relazione con la funzione base:
La funzione \(f(x) = \sqrt[3]{x-2} + 1\) si ottiene dalla funzione base \(g(x) = \sqrt[3]{x}\) tramite:
Il flesso di \(g(x) = \sqrt[3]{x}\), che si trova in \(O(0, 0)\), viene traslato in \(F(2, 1)\).
Conclusioni:
Comportamento agli estremi:
Nota didattica:
Questo esercizio dimostra che:
Il grafico della funzione è di questo tipo:
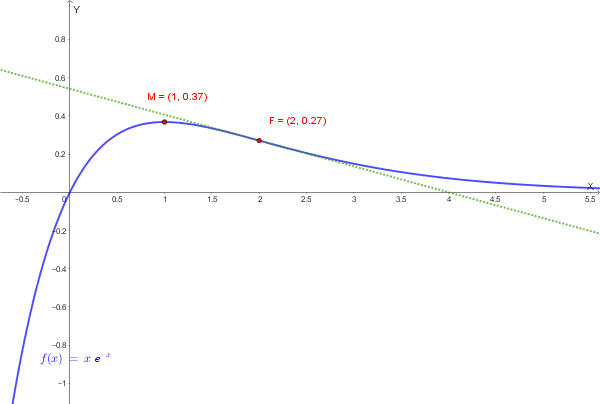
Studiare la concavità della seguente funzione esponenziale e determinare gli eventuali flessi:
\[f(x) = x e^{-x}\]Soluzione quesito 4:
Premessa importante:
Le funzioni che coinvolgono prodotti di polinomi ed esponenziali possono avere flessi. La presenza dell'esponenziale garantisce che tutte le derivate esistano in ogni punto del dominio.
Passo 1: Dominio
La funzione è definita per ogni \(x \in \mathbb{R}\):
\[D = \mathbb{R}\]Passo 2: Calcolo della derivata prima
Usando la regola del prodotto:
\[f'(x) = 1 \cdot e^{-x} + x \cdot (-e^{-x}) = e^{-x}(1 - x)\]Studio del segno di \(f'(x)\):
Poiché \(e^{-x} > 0\) per ogni \(x\), il segno di \(f'(x)\) dipende solo da \((1-x)\):
Punto estremante: \(x = 1\) è punto di massimo assoluto con \(f(1) = 1 \cdot e^{-1} = \frac{1}{e} \approx 0.368\)
Passo 3: Calcolo della derivata seconda
Deriviamo \(f'(x) = e^{-x}(1-x)\) usando la regola del prodotto:
\[f''(x) = (-e^{-x})(1-x) + e^{-x}(-1) = -e^{-x}(1-x) - e^{-x}\] \[f''(x) = e^{-x}[-(1-x) - 1] = e^{-x}[-1 + x - 1] = e^{-x}(x - 2)\]Passo 4: Studio del segno di \(f''(x)\)
Risolviamo \(f''(x) = 0\):
\[e^{-x}(x - 2) = 0\]Poiché \(e^{-x} > 0\) per ogni \(x\), abbiamo:
\[x - 2 = 0 \implies x = 2\]Studio del segno:
| Intervallo | \(f''(x)\) | Concavità |
|---|---|---|
| \(x < 2\) | − | Concava verso il basso (∩) |
| \(x = 2\) | 0 | - |
| \(x > 2\) | + | Concava verso l'alto (∪) |
Passo 5: Determinazione del flesso
Poiché la derivata seconda cambia segno in \(x = 2\), questo è un punto di flesso.
Calcoliamo le coordinate del punto di flesso:
\[f(2) = 2 \cdot e^{-2} = \frac{2}{e^2} \approx 0.271\]Calcolo della pendenza della tangente nel flesso:
\[f'(2) = e^{-2}(1-2) = -e^{-2} = -\frac{1}{e^2} \approx -0.135\]La tangente nel punto di flesso ha coefficiente angolare negativo (la funzione è decrescente in quel punto).
Conclusioni:
Comportamento agli estremi:
Asintoti:
Nota didattica:
Questo esercizio mostra che:
Il grafico della funzione è di questo tipo:
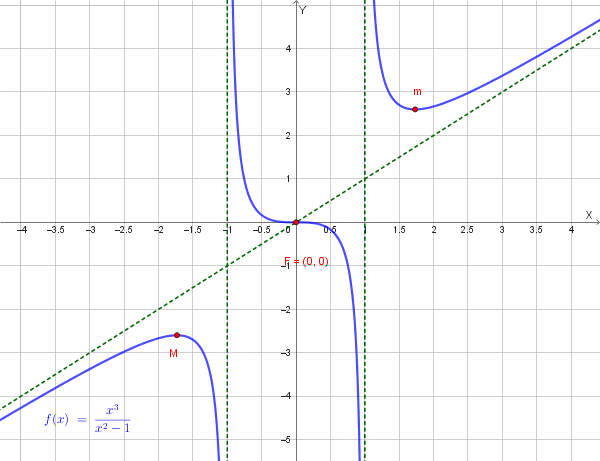
Dopo aver determinato il dominio della funzione
\[f(x) = \frac{x^3}{x^2 - 1}\]dimostra che la funzione è dispari, trova gli eventuali asintoti, individua gli eventuali massimi e minimi, studia la concavità, trova gli eventuali flessi e traccia un grafico qualitativo della funzione.
Soluzione quesito 5:
Premessa importante:
Le funzioni razionali fratte possono presentare flessi e asintoti obliqui. È importante studiare il comportamento della funzione sia nei punti di discontinuità che negli intervalli di continuità.
Passo 1: Dominio
Il denominatore si annulla per \(x^2 - 1 = 0\), cioè per \(x = \pm 1\).
\[D = \mathbb{R} \setminus \{-1, 1\} = (-\infty, -1) \cup (-1, 1) \cup (1, +\infty)\]Passo 2: Studio della parità
Verifichiamo se la funzione è pari o dispari calcolando \(f(-x)\):
\[f(-x) = \frac{(-x)^3}{(-x)^2-1} = \frac{-x^3}{x^2-1} = -\frac{x^3}{x^2-1} = -f(x)\]Poiché \(f(-x) = -f(x)\) per ogni \(x\) del dominio, la funzione è dispari.
Conseguenza: Il grafico è simmetrico rispetto all'origine. Questo significa che:
Passo 3: Studio degli asintoti
3a) Asintoti verticali
Studiamo i limiti nei punti di discontinuità:
3b) Asintoto obliquo
Poiché il grado del numeratore supera di 1 quello del denominatore, cerchiamo un asintoto obliquo.
Metodo 1: Divisione tra polinomi
Eseguiamo la divisione:
\[\frac{x^3}{x^2-1} = x + \frac{x}{x^2-1}\]Ricordiamo che: Se una funzione può essere scritta nella forma \(f(x) = mx + q + g(x)\) con \(g(x)\) infinitesimo per \(x \to \pm\infty\), allora \(y = mx + q\) è asintoto obliquo per \(x \to \pm\infty\).
Nel nostro caso:
Metodo 2: Calcolo diretto di \(m\) e \(q\)
Calcoliamo il coefficiente angolare:
\[m = \lim_{x \to \pm\infty} \frac{f(x)}{x} = \lim_{x \to \pm\infty} \frac{x^3}{x(x^2-1)} = \lim_{x \to \pm\infty} \frac{x^2}{x^2-1} = \lim_{x \to \pm\infty} \frac{x^2}{x^2(1-\frac{1}{x^2})} = 1\]Calcoliamo l'intercetta:
\[q = \lim_{x \to \pm\infty} [f(x) - mx] = \lim_{x \to \pm\infty} \left[\frac{x^3}{x^2-1} - x\right] = \lim_{x \to \pm\infty} \frac{x^3 - x(x^2-1)}{x^2-1} = \lim_{x \to \pm\infty} \frac{x}{x^2-1} = 0\]Asintoto obliquo: \(y = x\) (sia per \(x \to +\infty\) che per \(x \to -\infty\))
Passo 4: Studio della monotonia (massimi e minimi)
Calcolo della derivata prima
Usando la regola del quoziente:
\[f'(x) = \frac{3x^2(x^2-1) - x^3 \cdot 2x}{(x^2-1)^2} = \frac{3x^4 - 3x^2 - 2x^4}{(x^2-1)^2} = \frac{x^4 - 3x^2}{(x^2-1)^2}\] \[f'(x) = \frac{x^2(x^2 - 3)}{(x^2-1)^2}\]Studio del segno di \(f'(x)\):
Punti critici: \(x = 0\), \(x = \pm\sqrt{3}\) (e \(x = \pm 1\) non nel dominio)
| Intervallo | \(x^2\) | \(x^2-3\) | \((x^2-1)^2\) | \(f'(x)\) | Monotonia |
|---|---|---|---|---|---|
| \(x < -\sqrt{3}\) | + | + | + | + | Crescente |
| \(-\sqrt{3} < x < -1\) | + | − | + | − | Decrescente |
| \(-1 < x < 0\) | + | − | + | − | Decrescente |
| \(0 < x < 1\) | + | − | + | − | Decrescente |
| \(1 < x < \sqrt{3}\) | + | − | + | − | Decrescente |
| \(x > \sqrt{3}\) | + | + | + | + | Crescente |
Determinazione dei punti estremanti:
Nota: Per la simmetria dispari, se \(M\) è un massimo, il punto simmetrico rispetto all'origine è un minimo, come infatti verificato.
Passo 5: Studio della concavità
Calcolo della derivata seconda
Deriviamo \(f'(x) = \frac{x^4-3x^2}{(x^2-1)^2}\) usando la regola del quoziente:
\[f''(x) = \frac{(4x^3-6x)(x^2-1)^2 - (x^4-3x^2) \cdot 2(x^2-1) \cdot 2x}{(x^2-1)^4}\]Semplificando (raccogliendo \((x^2-1)\) al numeratore):
\[f''(x) = \frac{(4x^3-6x)(x^2-1) - 4x(x^4-3x^2)}{(x^2-1)^3}\] \[f''(x) = \frac{4x^5 - 4x^3 - 6x^3 + 6x - 4x^5 + 12x^3}{(x^2-1)^3}\] \[f''(x) = \frac{2x^3 + 6x}{(x^2-1)^3} = \frac{2x(x^2+3)}{(x^2-1)^3}\]Studio del segno di \(f''(x)\)
Analizziamo i fattori:
| Intervallo | \(2x\) | \(x^2+3\) | \((x^2-1)^3\) | \(f''(x)\) | Concavità |
|---|---|---|---|---|---|
| \(x < -1\) | − | + | + | − | Verso il basso (∩) |
| \(-1 < x < 0\) | − | + | − | + | Verso l'alto (∪) |
| \(0 < x < 1\) | + | + | − | − | Verso il basso (∩) |
| \(x > 1\) | + | + | + | + | Verso l'alto (∪) |
Passo 6: Determinazione dei flessi
La derivata seconda si annulla in \(x = 0\) e cambia segno (da positivo a negativo passando da sinistra a destra).
Calcoliamo le coordinate del punto:
\[f(0) = \frac{0^3}{0^2-1} = \frac{0}{-1} = 0\]Punto di flesso: \(F(0, 0)\)
Verifica che il flesso giace sull'asintoto:
Il punto \(F(0, 0)\) appartiene all'asintoto obliquo \(y = x\) perché \(0 = 0\). ✓
Questo è un fatto interessante: il flesso si trova esattamente sull'asintoto obliquo!
Inoltre, essendo la funzione dispari e avendo un flesso nell'origine, questo punto è anche centro di simmetria del grafico.
Passo 7: Grafico qualitativo
Riepilogo delle informazioni per il grafico:
Il grafico della funzione è di questo tipo:
Studia la seguente funzione:
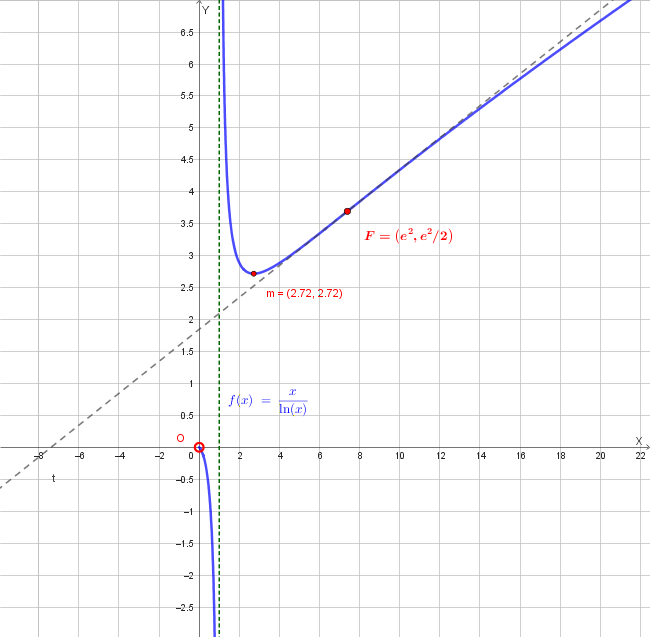
\[f(x) = \frac{x}{\ln(x)}\]indicando eventuali asintoti, eventuali massimi e minimi, eventuali flessi. Traccia un grafico qualitativo della funzione e trova l'equazione della tangente nel punto di ascissa \(x = e^2\).
Soluzione quesito 6:
Premessa importante:
Le funzioni logaritmiche possono presentare comportamenti interessanti, inclusi punti di flesso. In questo caso studieremo una funzione con un asintoto verticale particolare e un punto di minimo.
Passo 1: Dominio
La funzione è definita quando:
Passo 2: Studio degli asintoti
2a) Asintoto verticale in \(x = 0\)
\[\lim_{x \to 0^+} \frac{x}{\ln(x)} = \frac{0^+}{-\infty} = 0^-\]Non c'è asintoto verticale in \(x = 0\), ma la funzione tende a \(0\) da valori negativi.
2b) Asintoto verticale in \(x = 1\)
Studiamo i limiti destro e sinistro:
\[\lim_{x \to 1^-} \frac{x}{\ln(x)} = \frac{1}{0^-} = -\infty\] \[\lim_{x \to 1^+} \frac{x}{\ln(x)} = \frac{1}{0^+} = +\infty\]Asintoto verticale: \(x = 1\)
2c) Comportamento per \(x \to +\infty\)
\[\lim_{x \to +\infty} \frac{x}{\ln(x)} = +\infty\](Il numeratore cresce più velocemente del denominatore)
Verifichiamo se c'è un asintoto obliquo calcolando:
\[m = \lim_{x \to +\infty} \frac{f(x)}{x} = \lim_{x \to +\infty} \frac{x}{x\ln(x)} = \lim_{x \to +\infty} \frac{1}{\ln(x)} = 0\]Poiché \(m = 0\), non c'è asintoto obliquo. Verifichiamo l'asintoto orizzontale:
\[\lim_{x \to +\infty} f(x) = +\infty\]Non ci sono asintoti orizzontali né obliqui per \(x \to +\infty\).
Passo 3: Studio della monotonia (massimi e minimi)
Calcolo della derivata prima
Usando la regola del quoziente:
\[f'(x) = \frac{1 \cdot \ln(x) - x \cdot \frac{1}{x}}{[\ln(x)]^2} = \frac{\ln(x) - 1}{[\ln(x)]^2}\]Studio del segno di \(f'(x)\)
Il denominatore \([\ln(x)]^2 > 0\) per ogni \(x \in D\), quindi il segno dipende dal numeratore:
| Intervallo | \(\ln(x) - 1\) | \(f'(x)\) | Monotonia |
|---|---|---|---|
| \(0 < x < 1\) | − | − | Decrescente |
| \(1 < x < e\) | − | − | Decrescente |
| \(x > e\) | + | + | Crescente |
Determinazione del punto estremante:
\(x = e\) è punto di minimo relativo:
\[f(e) = \frac{e}{\ln(e)} = \frac{e}{1} = e \approx 2.718\]Punto: \(m(e, e)\)
Passo 4: Studio della concavità
Calcolo della derivata seconda
Deriviamo \(f'(x) = \frac{\ln(x) - 1}{[\ln(x)]^2}\) usando la regola del quoziente:
\[f''(x) = \frac{\frac{1}{x} \cdot [\ln(x)]^2 - (\ln(x) - 1) \cdot 2\ln(x) \cdot \frac{1}{x}}{[\ln(x)]^4}\]Semplificando (moltiplichiamo numeratore e denominatore per \(x\)):
\[f''(x) = \frac{[\ln(x)]^2 - 2\ln(x)(\ln(x) - 1)}{x[\ln(x)]^4} = \frac{[\ln(x)]^2 - 2[\ln(x)]^2 + 2\ln(x)}{x[\ln(x)]^4}\] \[f''(x) = \frac{-[\ln(x)]^2 + 2\ln(x)}{x[\ln(x)]^4} = \frac{\ln(x)(2 - \ln(x))}{x[\ln(x)]^4} = \frac{2 - \ln(x)}{x[\ln(x)]^3}\]Studio del segno di \(f''(x)\)
Analizziamo i fattori:
| Intervallo | \(2 - \ln(x)\) | \(x\) | \([\ln(x)]^3\) | \(f''(x)\) | Concavità |
|---|---|---|---|---|---|
| \(0 < x < 1\) | + | + | − | − | Verso il basso (∩) |
| \(1 < x < e^2\) | + | + | + | + | Verso l'alto (∪) |
| \(x > e^2\) | − | + | + | − | Verso il basso (∩) |
Passo 5: Determinazione del flesso
La derivata seconda cambia segno in \(x = e^2\), quindi questo è un punto di flesso.
Calcoliamo le coordinate del punto:
\[f(e^2) = \frac{e^2}{\ln(e^2)} = \frac{e^2}{2} \approx 3.695\]Punto di flesso: \(F\left(e^2, \frac{e^2}{2}\right)\)
Passo 6: Equazione della tangente in \(x = e^2\)
L'equazione della tangente nel punto di ascissa \(x_0\) è:
\[y - f(x_0) = f'(x_0)(x - x_0)\]Calcoliamo \(f'(e^2)\):
\[f'(e^2) = \frac{\ln(e^2) - 1}{[\ln(e^2)]^2} = \frac{2 - 1}{2^2} = \frac{1}{4}\]Sostituiamo nell'equazione della tangente:
\[y - \frac{e^2}{2} = \frac{1}{4}(x - e^2)\] \[y = \frac{1}{4}x - \frac{e^2}{4} + \frac{e^2}{2}\] \[y = \frac{1}{4}x + \frac{e^2}{4}\]Equazione della tangente: \(y = \frac{1}{4}x + \frac{e^2}{4}\) oppure \(y = \frac{1}{4}(x + e^2)\)
Nota: La tangente nel punto di flesso ha coefficiente angolare positivo, il che conferma che la funzione è crescente in quel punto (infatti \(e^2 > e\)).
Riepilogo:
Il grafico della funzione è di questo tipo:
È data la funzione:
\[f(x) = \frac{\sin(x)}{2 + \cos(x)}\]Soluzione quesito 7:
Premessa importante:
Le funzioni goniometriche hanno proprietà di periodicità e simmetria che semplificano lo studio. È importante verificare queste proprietà prima di procedere con l'analisi completa.
Dominio
La funzione è definita quando il denominatore è diverso da zero:
\[2 + \cos(x) \neq 0 \implies \cos(x) \neq -2\]Poiché \(-1 \leq \cos(x) \leq 1\) per ogni \(x \in \mathbb{R}\), la condizione \(\cos(x) \neq -2\) è sempre verificata.
\[D = \mathbb{R}\]1) Dimostrazione che la funzione ha periodo \(2\pi\)
Una funzione \(f(x)\) ha periodo \(T\) se \(f(x + T) = f(x)\) per ogni \(x\) del dominio.
Verifichiamo che \(f(x + 2\pi) = f(x)\):
\[f(x + 2\pi) = \frac{\sin(x + 2\pi)}{2 + \cos(x + 2\pi)}\]Usando le proprietà delle funzioni goniometriche:
Quindi:
\[f(x + 2\pi) = \frac{\sin(x)}{2 + \cos(x)} = f(x)\]Conclusione: La funzione ha periodo \(2\pi\). ✓
Verifica che \(2\pi\) sia il periodo minimo:
Il periodo di \(\sin(x)\) è \(2\pi\) e il periodo di \(\cos(x)\) è \(2\pi\). Il periodo della loro combinazione è il minimo comune multiplo dei periodi, che è \(2\pi\).
2) Studio della parità
Verifichiamo se la funzione è pari (\(f(-x) = f(x)\)) o dispari (\(f(-x) = -f(x)\)).
Calcoliamo \(f(-x)\):
\[f(-x) = \frac{\sin(-x)}{2 + \cos(-x)}\]Usando le proprietà delle funzioni goniometriche:
Quindi:
\[f(-x) = \frac{-\sin(x)}{2 + \cos(x)} = -\frac{\sin(x)}{2 + \cos(x)} = -f(x)\]Conclusione: La funzione è dispari. ✓
Conseguenza: Il grafico è simmetrico rispetto all'origine. Questo significa che:
3) Studio della funzione in \([0, 2\pi]\)
Passo 1: Calcolo della derivata prima
Usando la regola del quoziente:
\[f'(x) = \frac{\cos(x) \cdot (2 + \cos(x)) - \sin(x) \cdot (-\sin(x))}{(2 + \cos(x))^2}\] \[f'(x) = \frac{2\cos(x) + \cos^2(x) + \sin^2(x)}{(2 + \cos(x))^2}\]Usando l'identità fondamentale \(\sin^2(x) + \cos^2(x) = 1\):
\[f'(x) = \frac{2\cos(x) + 1}{(2 + \cos(x))^2}\]Studio del segno di \(f'(x)\)
Il denominatore \((2 + \cos(x))^2 > 0\) per ogni \(x\), quindi il segno dipende dal numeratore:
\[2\cos(x) + 1 = 0 \implies \cos(x) = -\frac{1}{2}\]In \([0, 2\pi]\), le soluzioni sono:
\[x = \frac{2\pi}{3}, \quad x = \frac{4\pi}{3}\]| Intervallo | \(\cos(x)\) | \(2\cos(x) + 1\) | \(f'(x)\) | Monotonia |
|---|---|---|---|---|
| \(0 < x < \frac{2\pi}{3}\) | \(> -\frac{1}{2}\) | + | + | Crescente |
| \(\frac{2\pi}{3} < x < \frac{4\pi}{3}\) | \(< -\frac{1}{2}\) | − | − | Decrescente |
| \(\frac{4\pi}{3} < x < 2\pi\) | \(> -\frac{1}{2}\) | + | + | Crescente |
Determinazione dei punti estremanti:
Calcoliamo il valore:
\[f\left(\frac{2\pi}{3}\right) = \frac{\sin\left(\frac{2\pi}{3}\right)}{2 + \cos\left(\frac{2\pi}{3}\right)} = \frac{\frac{\sqrt{3}}{2}}{2 - \frac{1}{2}} = \frac{\frac{\sqrt{3}}{2}}{\frac{3}{2}} = \frac{\sqrt{3}}{3}\]Punto: \(M\left(\frac{2\pi}{3}, \frac{\sqrt{3}}{3}\right)\)
Calcoliamo il valore:
\[f\left(\frac{4\pi}{3}\right) = \frac{\sin\left(\frac{4\pi}{3}\right)}{2 + \cos\left(\frac{4\pi}{3}\right)} = \frac{-\frac{\sqrt{3}}{2}}{2 - \frac{1}{2}} = \frac{-\frac{\sqrt{3}}{2}}{\frac{3}{2}} = -\frac{\sqrt{3}}{3}\]Punto: \(m\left(\frac{4\pi}{3}, -\frac{\sqrt{3}}{3}\right)\)
Passo 2: Calcolo della derivata seconda
Deriviamo \(f'(x) = \frac{2\cos(x) + 1}{(2 + \cos(x))^2}\):
\[f''(x) = \frac{-2\sin(x) \cdot (2 + \cos(x))^2 - (2\cos(x) + 1) \cdot 2(2 + \cos(x)) \cdot (-\sin(x))}{(2 + \cos(x))^4}\]Semplificando (raccogliendo \((2 + \cos(x))\) e \(-\sin(x)\)):
\[f''(x) = \frac{-\sin(x) \cdot [(2 + \cos(x)) \cdot 2 - (2\cos(x) + 1) \cdot 2]}{(2 + \cos(x))^3}\] \[f''(x) = \frac{-\sin(x) \cdot [4 + 2\cos(x) - 4\cos(x) - 2]}{(2 + \cos(x))^3}\] \[f''(x) = \frac{-\sin(x) \cdot [2 - 2\cos(x)]}{(2 + \cos(x))^3}\] \[f''(x) = \frac{-2\sin(x)(1 - \cos(x))}{(2 + \cos(x))^3}\]Studio del segno di \(f''(x)\) in \([0, 2\pi]\)
Analizziamo i fattori:
| Intervallo | \(-2\) | \(\sin(x)\) | \(1-\cos(x)\) | \((2+\cos(x))^3\) | \(f''(x)\) | Concavità |
|---|---|---|---|---|---|---|
| \(0 < x < \pi\) | − | + | + | + | − | Verso il basso (∩) |
| \(\pi < x < 2\pi\) | − | − | + | + | + | Verso l'alto (∪) |
Passo 3: Determinazione dei flessi
La derivata seconda si annulla quando \(\sin(x) = 0\) oppure \(1 - \cos(x) = 0\).
In \([0, 2\pi]\):
Verifichiamo quali sono effettivamente flessi (cambio di concavità):
Punto di flesso: \(F(\pi, 0)\)
Nota sulla funzione dispari: Poiché la funzione è dispari e passa per l'origine, il punto \((0, 0)\) è centro di simmetria del grafico. Il flesso in \((\pi, 0)\) è coerente con questa simmetria.
4) Grafico qualitativo
Riepilogo per il grafico:
Il grafico della funzione è di questo tipo:
![Grafico della funzione f(x) = sin(x)/(2+cos(x)) nell'intervallo [0,2π]](quesito7.png)
Considera la seguente funzione:
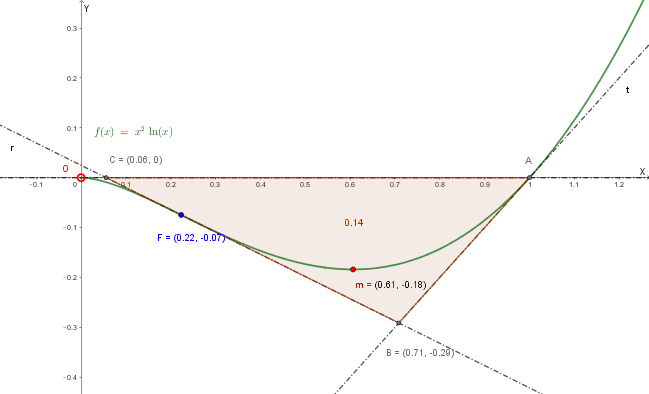
\[f(x) = x^2 \ln(x)\]Soluzione quesito 8:
Premessa importante:
Le funzioni che coinvolgono prodotti di polinomi e logaritmi presentano comportamenti interessanti, specialmente vicino allo zero. Il limite notevole \(\lim_{x \to 0^+} x^a \ln(x) = 0\) per \(a > 0\) è fondamentale per lo studio.
1) Dominio e limiti agli estremi
Dominio:
La funzione è definita quando \(\ln(x)\) esiste, cioè per \(x > 0\).
\[D = (0, +\infty)\]Limiti agli estremi del dominio:
a) Limite per \(x \to 0^+\):
\[\lim_{x \to 0^+} x^2 \ln(x)\]Questa è una forma indeterminata del tipo \(0 \cdot (-\infty)\). Riscriviamo come:
\[\lim_{x \to 0^+} x^2 \ln(x) = \lim_{x \to 0^+} \frac{\ln(x)}{\frac{1}{x^2}}\]Ora abbiamo la forma \(\frac{-\infty}{+\infty}\). Applichiamo la regola di De L'Hôpital:
\[\lim_{x \to 0^+} \frac{\ln(x)}{\frac{1}{x^2}} = \lim_{x \to 0^+} \frac{\frac{1}{x}}{-\frac{2}{x^3}} = \lim_{x \to 0^+} \frac{x^3}{-2x} = \lim_{x \to 0^+} \frac{x^2}{-2} = 0^-\]Oppure usando il limite notevole:
Si può dimostrare che per ogni \(a > 0\): \(\lim_{x \to 0^+} x^a \ln(x) = 0^-\)
Nel nostro caso \(a = 2 > 0\), quindi:
\[\lim_{x \to 0^+} x^2 \ln(x) = 0^-\]Interpretazione: Il termine \(x^2\) (che tende a 0) "vince" sul termine \(\ln(x)\) (che tende a \(-\infty\)).
b) Limite per \(x \to +\infty\):
\[\lim_{x \to +\infty} x^2 \ln(x) = +\infty\]Entrambi i fattori tendono a \(+\infty\), quindi il prodotto tende a \(+\infty\).
Conclusioni sui limiti:
2) Ricerca di massimi e minimi
Calcolo della derivata prima
Usando la regola del prodotto:
\[f'(x) = 2x \ln(x) + x^2 \cdot \frac{1}{x} = 2x \ln(x) + x = x(2\ln(x) + 1)\]2a) Metodo 1: Studio del segno della derivata prima
Cerchiamo dove \(f'(x) = 0\):
\[x(2\ln(x) + 1) = 0\]Le soluzioni sono:
Studio del segno di \(f'(x) = x(2\ln(x) + 1)\):
| Intervallo | \(x\) | \(2\ln(x) + 1\) | \(f'(x)\) | Monotonia |
|---|---|---|---|---|
| \(0 < x < e^{-1/2}\) | + | − | − | Decrescente |
| \(x > e^{-1/2}\) | + | + | + | Crescente |
Conclusione con il metodo della derivata prima:
La funzione passa da decrescente a crescente in \(x = e^{-1/2} = \frac{1}{\sqrt{e}}\), quindi questo è un punto di minimo assoluto.
Calcoliamo il valore:
\[f\left(e^{-1/2}\right) = \left(e^{-1/2}\right)^2 \cdot \ln\left(e^{-1/2}\right) = e^{-1} \cdot \left(-\frac{1}{2}\right) = -\frac{1}{2e}\]Punto di minimo: \(m\left(\frac{1}{\sqrt{e}}, -\frac{1}{2e}\right) \approx (0.606, -0.184)\)
2b) Metodo 2: Metodo delle derivate successive
Il metodo delle derivate successive si usa quando una derivata si annulla in un punto ma non fornisce informazioni immediate sul tipo di punto critico.
Calcolo della derivata seconda:
Deriviamo \(f'(x) = 2x\ln(x) + x\):
\[f''(x) = 2\ln(x) + 2x \cdot \frac{1}{x} + 1 = 2\ln(x) + 2 + 1 = 2\ln(x) + 3\]Verifichiamo il valore nel punto critico \(x = e^{-1/2}\):
\[f''\left(e^{-1/2}\right) = 2\ln\left(e^{-1/2}\right) + 3 = 2 \cdot \left(-\frac{1}{2}\right) + 3 = -1 + 3 = 2 > 0\]Conclusione:
Poiché \(f'(e^{-1/2}) = 0\) e \(f''(e^{-1/2}) = 2 > 0\), il punto \(x = e^{-1/2}\) è un minimo. ✓
Nota sul metodo delle derivate successive:
Se fosse stato \(f''(x_0) = 0\), avremmo dovuto calcolare \(f'''(x_0)\). In generale:
3) Ricerca dei flessi
Abbiamo già calcolato:
\[f''(x) = 2\ln(x) + 3\]3a) Metodo 1: Studio del segno della derivata seconda
Cerchiamo dove \(f''(x) = 0\):
\[2\ln(x) + 3 = 0 \implies \ln(x) = -\frac{3}{2} \implies x = e^{-3/2}\]Studio del segno di \(f''(x)\):
| Intervallo | \(2\ln(x) + 3\) | \(f''(x)\) | Concavità |
|---|---|---|---|
| \(0 < x < e^{-3/2}\) | − | − | Verso il basso (∩) |
| \(x > e^{-3/2}\) | + | + | Verso l'alto (∪) |
Conclusione:
La derivata seconda cambia segno in \(x = e^{-3/2}\), quindi questo è un punto di flesso.
Calcoliamo le coordinate:
\[f\left(e^{-3/2}\right) = \left(e^{-3/2}\right)^2 \cdot \ln\left(e^{-3/2}\right) = e^{-3} \cdot \left(-\frac{3}{2}\right) = -\frac{3}{2e^3}\]Punto di flesso: \(F\left(e^{-3/2}, -\frac{3}{2e^3}\right) \approx (0.223, -0.075)\)
3b) Metodo 2: Metodo delle derivate successive
Nel punto \(x = e^{-3/2}\) abbiamo \(f''(e^{-3/2}) = 0\). Verifichiamo con la derivata terza.
Calcolo della derivata terza:
Deriviamo \(f''(x) = 2\ln(x) + 3\):
\[f'''(x) = \frac{2}{x}\]Valutiamo nel punto critico:
\[f'''\left(e^{-3/2}\right) = \frac{2}{e^{-3/2}} = 2e^{3/2} > 0\]Conclusione:
Poiché \(f''(e^{-3/2}) = 0\) e \(f'''(e^{-3/2}) \neq 0\) (la terza derivata, di ordine dispari, è la prima non nulla), il punto \(x = e^{-3/2}\) è un flesso. ✓
4) Coefficiente angolare della tangente all'origine
Dobbiamo trovare il coefficiente angolare della tangente lungo la quale il grafico si avvicina all'origine.
Il coefficiente angolare della tangente in un punto è dato dalla derivata. Poiché la funzione si avvicina all'origine per \(x \to 0^+\), calcoliamo:
\[m = \lim_{x \to 0^+} f'(x) = \lim_{x \to 0^+} x(2\ln(x) + 1)\]Questa è una forma indeterminata \(0 \cdot (-\infty)\). Riscriviamo:
\[m = \lim_{x \to 0^+} \frac{2\ln(x) + 1}{\frac{1}{x}}\]Forma \(\frac{-\infty}{+\infty}\). Applichiamo De L'Hôpital:
\[m = \lim_{x \to 0^+} \frac{\frac{2}{x}}{-\frac{1}{x^2}} = \lim_{x \to 0^+} \frac{2x^2}{-x} = \lim_{x \to 0^+} (-2x) = 0\]Risposta: Il coefficiente angolare della tangente lungo la quale il grafico si avvicina all'origine è \(m = 0\).
Interpretazione: Il grafico si avvicina all'origine tangenzialmente all'asse delle \(x\) (tangente orizzontale).
5) Area del triangolo
Punto A: Intersezione del grafico con l'asse delle \(x\)
Risolviamo \(f(x) = 0\):
\[x^2 \ln(x) = 0\]Poiché \(x > 0\) nel dominio, deve essere \(\ln(x) = 0\), quindi \(x = 1\).
Punto A: \(A(1, 0)\)
Tangente t in A:
Calcoliamo \(f'(1)\):
\[f'(1) = 1 \cdot (2\ln(1) + 1) = 1 \cdot (0 + 1) = 1\]Equazione della tangente in \(A(1, 0)\):
\[y - 0 = 1(x - 1) \implies y = x - 1\]Tangente t: \(y = x - 1\)
Punto F: Flesso già trovato
\(F\left(e^{-3/2}, -\frac{3}{2e^3}\right)\)
Tangente r in F:
Calcoliamo \(f'(e^{-3/2})\):
\[f'\left(e^{-3/2}\right) = e^{-3/2}\left(2\ln(e^{-3/2}) + 1\right) = e^{-3/2}\left(2 \cdot \left(-\frac{3}{2}\right) + 1\right)\] \[= e^{-3/2}(-3 + 1) = -2e^{-3/2}\]Equazione della tangente in \(F\):
\[y - \left(-\frac{3}{2e^3}\right) = -2e^{-3/2}\left(x - e^{-3/2}\right)\] \[y + \frac{3}{2e^3} = -2e^{-3/2}x + 2e^{-3/2} \cdot e^{-3/2}\] \[y + \frac{3}{2e^3} = -2e^{-3/2}x + 2e^{-3}\] \[y = -2e^{-3/2}x + 2e^{-3} - \frac{3}{2e^3}\] \[y = -2e^{-3/2}x + \frac{4}{2e^3} - \frac{3}{2e^3}\] \[y = -2e^{-3/2}x + \frac{1}{2e^3}\]Tangente r: \(y = -2e^{-3/2}x + \frac{1}{2e^3}\)
Vertici del triangolo:
Vertice 1: Intersezione di \(t\) con l'asse \(x\)
\(y = x - 1 = 0 \implies x = 1\)
Vertice: \(V_1(1, 0)\) (che è il punto A)
Vertice 2: Intersezione di \(r\) con l'asse \(x\)
\(y = -2e^{-3/2}x + \frac{1}{2e^3} = 0\)
\[2e^{-3/2}x = \frac{1}{2e^3}\] \[x = \frac{1}{2e^3 \cdot 2e^{-3/2}} = \frac{1}{4e^{3-3/2}} = \frac{1}{4e^{3/2}}\]Vertice: \(V_2\left(\frac{1}{4e^{3/2}}, 0\right)\) (che è il punto C)
Vertice 3: Intersezione tra \(t\) e \(r\) (punto B)
Risolviamo il sistema:
\[\begin{cases} y = x - 1 \\ y = -2e^{-3/2}x + \frac{1}{2e^3} \end{cases}\]Uguagliando:
\[x - 1 = -2e^{-3/2}x + \frac{1}{2e^3}\] \[x + 2e^{-3/2}x = 1 + \frac{1}{2e^3}\] \[x(1 + 2e^{-3/2}) = 1 + \frac{1}{2e^3}\] \[x = \frac{1 + \frac{1}{2e^3}}{1 + 2e^{-3/2}} = \frac{\frac{2e^3 + 1}{2e^3}}{1 + 2e^{-3/2}}\]Semplifichiamo il denominatore:
\[1 + 2e^{-3/2} = \frac{e^{3/2} + 2}{e^{3/2}}\]Quindi:
\[x = \frac{\frac{2e^3 + 1}{2e^3}}{\frac{e^{3/2} + 2}{e^{3/2}}} = \frac{2e^3 + 1}{2e^3} \cdot \frac{e^{3/2}}{e^{3/2} + 2} = \frac{(2e^3 + 1)e^{3/2}}{2e^3(e^{3/2} + 2)}\]Calcoliamo \(y = x - 1\).
Calcolo dell'area del triangolo:
Il triangolo ha base sull'asse \(x\) tra \(V_1(1, 0)\) e \(V_2\left(\frac{1}{4e^{3/2}}, 0\right)\).
Base del triangolo:
\[b = 1 - \frac{1}{4e^{3/2}} = \frac{4e^{3/2} - 1}{4e^{3/2}}\]L'altezza è la distanza del vertice \(V_3\) (B) dall'asse \(x\), cioè l'ordinata \(y\) di \(V_3\), cioè B, in valore assoluto.
Poiché due vertici del triangolo (A e C) stanno sull'asse \(x\), possiamo calcolare l'are nel seguente modo:
\[\text{Area} = \frac{1}{2} \cdot \text{base} \cdot \text{altezza}\]Dove base = \(|x_A - x_C|\) e altezza = \(|y_B|\).
Sostituendo \(x_B = \frac{(2e^3 + 1)e^{3/2}}{2e^3(e^{3/2} + 2)}\) in \(y = x - 1\):
\[y_B = \frac{(2e^3 + 1)e^{3/2}}{2e^3(e^{3/2} + 2)} - 1 = \frac{(2e^3 + 1)e^{3/2} - 2e^3(e^{3/2} + 2)}{2e^3(e^{3/2} + 2)}\] \[y_B = \frac{(2e^3 + 1)e^{3/2} - 2e^3 \cdot e^{3/2} - 4e^3}{2e^3(e^{3/2} + 2)} = \frac{2e^3 \cdot e^{3/2} + e^{3/2} - 2e^3 \cdot e^{3/2} - 4e^3}{2e^3(e^{3/2} + 2)}\] \[y_B = \frac{e^{3/2} - 4e^3}{2e^3(e^{3/2} + 2)} = \frac{e^{3/2}(1 - 4e^{3/2})}{2e^3(e^{3/2} + 2)}\]Semplificando:
\[y_B = \frac{1 - 4e^{3/2}}{2e^{3/2}(e^{3/2} + 2)}\]Poiché \(4e^{3/2} > 1\), abbiamo \(y_B < 0 \)
Vertice B: \(B\left(\frac{(2e^3 + 1)e^{3/2}}{2e^3(e^{3/2} + 2)}, \frac{1 - 4e^{3/2}}{2e^{3/2}(e^{3/2} + 2)}\right)\)
Riepilogando, i vertici del triangolo sono:
Calcolo dell'area:
L'area del triangolo è quindi:
\[\text{Area} = \frac{1}{2}|x_A - x_C| \cdot |y_B|\]Risultato finale (dopo i calcoli):
Area esatta: \(\text{Area} = \frac{1}{8e^3}(4e^{3/2} - 1)^2\)
Area approssimata: \(\text{Area} \approx 0.14\)
Grafico qualitativo della funzione: