



Studia la funzione e controlla la soluzione guidata dei vari punti cliccando sul bottone corrispondente. Premi il bottone RIPRISTINA per cancellare gli output.
È sufficiente studiare la funzione \( g(x) = x^2 - 4 \ln(x+1) \). Il dominio di \( g(x) \) è determinato dalla condizione \( x + 1 > 0 \), quindi \( x > -1 \). Il dominio di \( f(x) = |g(x)| \) è lo stesso: \( (-1, +\infty) \).
Il dominio \( (-1, +\infty) \) non è simmetrico rispetto all'origine, quindi la funzione \( f(x) \) non è né pari né dispari.
(Grafico schematico che mostra le intersezioni approssimative di \( y=x^2 \) e \( y=4\ln(x+1) \))
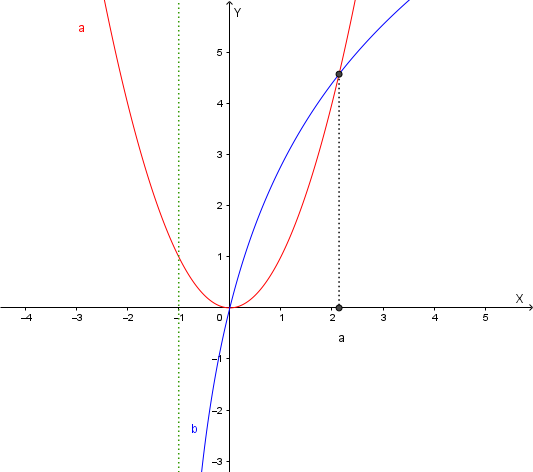
Dal confronto grafico si deduce che le due funzioni si intersecano in \( x = 0 \) e in un altro punto \( c \) compreso tra 2 e 3. Questi sono i punti in cui \( f(x) = 0 \), quindi le intersezioni con l'asse x sono approssimativamente \( (0, 0) \) e \( (c, 0) \) con \( 2 < c < 3 \).
Per studiare il segno di \( g(x) > 0 \), analizziamo graficamente la disequazione \( x^2 > 4 \ln(x+1) \). Consideriamo le funzioni \( a(x) = x^2 \) e \( b(x) = 4 \ln(x+1) \) e osserviamo dove il grafico di \( a(x) \) si trova al di sopra del grafico di \( b(x) \).

(Grafico di confronto tra \( y = x^2 \) e \( y = 4 \ln(x+1) \))
Dal grafico di confronto, possiamo dedurre il segno di \( g(x) \):
In sintesi:
La derivata prima di \( g(x) \) è:
\[ g'(x) = 2x - \frac{4}{x+1} = \frac{2(x+2)(x-1)}{x+1} \]Studio del segno di \( g'(x) \):
Nel dominio \( (-1, +\infty) \), il denominatore \( (x+1) \) è sempre positivo. Il segno di \( g'(x) \) dipende dal segno del numeratore \( 2(x+2)(x-1) \).
Minimo locale in \( x = 1 \), con valore \( g(1) = 1 - 4 \ln(2) \).
La derivata seconda di \( g(x) \) è:
\[ g''(x) = 2 + \frac{4}{(x+1)^2} = \frac{2x^2 + 4x + 6}{(x+1)^2} \]Studio del segno di \( g''(x) \):
Nel dominio \( (-1, +\infty) \), il denominatore \( (x+1)^2 \) è sempre positivo.
Consideriamo il numeratore \( 2x^2 + 4x + 6 \). Il discriminante è \( \Delta = 4^2 - 4(2)(6) = -32 \). Poiché il discriminante è negativo e il coefficiente del termine di secondo grado è positivo, il numeratore è sempre positivo per ogni \( x \).
Pertanto, \( g''(x) > 0 \) per ogni \( x \) nel dominio \( (-1, +\infty) \). Questo significa che il grafico della funzione \( g(x) \) volge sempre la concavità verso l'alto. Non ci sono punti di flesso.
Per calcolare \( g'(x) \), applichiamo la regola della derivata del quoziente: \( \left(\frac{u}{v}\right)' = \frac{u'v - uv'}{v^2} \).
Sostituendo nella formula:
$$g'(x) = \frac{(1)(x^2 - 4) - (x)(2x)}{(x^2 - 4)^2}$$ $$g'(x) = \frac{x^2 - 4 - 2x^2}{(x^2 - 4)^2}$$ $$g'(x) = \boxed{\frac{-x^2 - 4}{(x^2 - 4)^2}}$$Per determinare la monotonia di \( g(x) \), analizziamo il segno di \( g'(x) \).
Poiché \( g'(x) \) è il rapporto tra un valore sempre negativo e un valore sempre positivo, la sua frazione è **sempre negativa** in tutto il dominio di \( g(x) \).
Di conseguenza, \( g'(x) < 0 \) per ogni \( x \) nel dominio di \( g(x) \). Ciò significa che la funzione \( g(x) \) è **sempre decrescente** nel suo dominio.
Questo studio è fondamentale per capire la monotonia della funzione \( f(x) = |g(x)| \).
Partiamo dalla derivata prima \( g'(x) = \frac{-x^2 - 4}{(x^2 - 4)^2} \).
Applichiamo nuovamente la regola della derivata del quoziente: \( \left(\frac{u}{v}\right)' = \frac{u'v - uv'}{v^2} \), dove \( u = -x^2 - 4 \) e \( v = (x^2 - 4)^2 \).
Sostituendo nella formula:
$$g''(x) = \frac{(-2x)(x^2 - 4)^2 - (-x^2 - 4)(4x(x^2 - 4))}{((x^2 - 4)^2)^2}$$Raccogliamo il fattore comune \( (x^2 - 4) \) al numeratore e semplifichiamo con il denominatore:
$$g''(x) = \frac{(x^2 - 4)[(-2x)(x^2 - 4) - (-x^2 - 4)(4x)]}{(x^2 - 4)^4}$$ $$g''(x) = \frac{-2x(x^2 - 4) - 4x(-x^2 - 4)}{(x^2 - 4)^3}$$Espandiamo e sommiamo i termini al numeratore:
$$g''(x) = \frac{-2x^3 + 8x + 4x^3 + 16x}{(x^2 - 4)^3}$$ $$g''(x) = \frac{2x^3 + 24x}{(x^2 - 4)^3}$$Raccogliamo \( 2x \) al numeratore:
$$g''(x) = \boxed{\frac{2x(x^2 + 12)}{(x^2 - 4)^3}}$$Il segno di \( g''(x) \) determina la concavità di \( g(x) \). Analizziamo il segno del numeratore e del denominatore separatamente:
| Intervallo | Segno di \( 2x \) | Segno di \( (x^2 - 4)^3 \) | Segno di \( g''(x) \) | Concavità di \( g(x) \) |
|---|---|---|---|---|
| \( x < -2 \) | \( - \) | \( + \) | \( - \) | Verso il basso |
| \( -2 < x < 0 \) | \( - \) | \( - \) | \( + \) | Verso l'alto |
| \( x = 0 \) | \( 0 \) | \( - \) | \( 0 \) | Punto di Flesso |
| \( 0 < x < 2 \) | \( + \) | \( - \) | \( - \) | Verso il basso |
| \( x > 2 \) | \( + \) | \( + \) | \( + \) | Verso l'alto |
Punti di flesso: Si ha un cambiamento di concavità in \( x = 0 \). La funzione \( g(x) \) è definita in \( x=0 \).
Il dominio della funzione \( f(x) = \frac{e^x}{|x| - 1} \) è l'insieme di tutti i numeri reali \( x \) per cui il denominatore \( |x| - 1 \) è diverso da zero.
Risolvendo \( |x| - 1 = 0 \), otteniamo \( |x| = 1 \), che implica \( x = 1 \) o \( x = -1 \).
Pertanto, il dominio della funzione è \( \mathbb{R} \setminus \{-1, 1\} \).
Studiamo la parità o disparità della funzione calcolando \( f(-x) \):
\( f(-x) = \frac{e^{-x}}{|{-x}| - 1} = \frac{e^{-x}}{|x| - 1} \).
Poiché \( f(-x) \neq f(x) \) e \( f(-x) \neq -f(x) \), la funzione non è né pari né dispari. Non presenta simmetrie rispetto all'asse y o all'origine.
Valutando \( f(0) = \frac{e^0}{|0| - 1} = \frac{1}{-1} = -1 \). Il punto di intersezione con l'asse y è \( (0, -1) \).
Risolviamo l'equazione \( f(x) = \frac{e^x}{|x| - 1} = 0 \). Poiché \( e^x \) è sempre positivo, l'equazione non ha soluzioni reali. Pertanto, non ci sono intersezioni con l'asse x.
Il segno di \( f(x) = \frac{e^x}{|x| - 1} \) dipende dal segno del denominatore \( |x| - 1 \), poiché il numeratore \( e^x \) è sempre positivo.
| Intervallo | \( |x| - 1 \) | \( f(x) \) |
|---|---|---|
| \( x < -1 \) | \( > 0 \) | \( > 0 \) |
| \( x = -1 \) | Nullo | Non definita |
| \( -1 < x < 1 \) | \( < 0 \) | \( < 0 \) |
| \( x = 1 \) | Nullo | Non definita |
| \( x > 1 \) | \( > 0 \) | \( > 0 \) |
Quando \( x \) si avvicina a \( -1 \), siamo nell'intervallo \( x < 0 \), quindi usiamo la forma \( f(x) = \frac{e^x}{-x - 1} \).
Analizziamo numeratore e denominatore separatamente:
Questo suggerisce un asintoto verticale in \( x = -1 \).
Anche questo conferma un asintoto verticale in \( x = -1 \).
Quando \( x \) si avvicina a \( 1 \), siamo nell'intervallo \( x > 0 \), quindi usiamo la forma \( f(x) = \frac{e^x}{x - 1} \).
Questo suggerisce un asintoto verticale in \( x = 1 \).
Anche questo conferma un asintoto verticale in \( x = 1 \).
Quando \( x \to +\infty \), siamo nell'intervallo \( x > 0 \), quindi usiamo la forma \( f(x) = \frac{e^x}{x - 1} \).
$$\lim_{x \to +\infty} f(x) = \lim_{x \to +\infty} \frac{e^x}{x - 1}$$Questa è una forma indeterminata del tipo \( \frac{\infty}{\infty} \). Applichiamo il Teorema di De L'Hôpital (o consideriamo gli ordini di infinito, sapendo che l'esponenziale cresce più velocemente di qualsiasi potenza di \(x\)):
$$\lim_{x \to +\infty} \frac{\frac{d}{dx}(e^x)}{\frac{d}{dx}(x - 1)} = \lim_{x \to +\infty} \frac{e^x}{1} = +\infty$$Poiché il limite tende a \(+\infty\), non ci sono asintoti orizzontali a destra. Dobbiamo verificare la presenza di asintoti obliqui.
Quando \( x \to -\infty \), siamo nell'intervallo \( x < 0 \), quindi usiamo la forma \( f(x) = \frac{e^x}{-x - 1} \).
$$\lim_{x \to -\infty} f(x) = \lim_{x \to -\infty} \frac{e^x}{-x - 1}$$Poiché il limite tende a un valore finito (\(0\)), la retta \( y = 0 \) (l'asse x) è un **asintoto orizzontale** per \( x \to -\infty \).
Come calcolato nei limiti, la funzione presenta asintoti verticali nei punti in cui il denominatore si annulla e il limite tende a infinito:
Quindi, le rette \( \mathbf{x = -1} \) e \( \mathbf{x = 1} \) sono **asintoti verticali**.
Verifichiamo il comportamento della funzione quando \( x \) tende all'infinito:
Un asintoto obliquo, della forma \( y = mx + q \), potrebbe esistere se \( \lim_{x \to \pm \infty} f(x) = \pm \infty \).
Dobbiamo calcolare il coefficiente angolare \( m = \lim_{x \to \pm \infty} \frac{f(x)}{x} \).
Consideriamo il caso per \( \mathbf{x \to +\infty} \):
Per \( x > 0 \), la funzione è \( f(x) = \frac{e^x}{x - 1} \).
$$m = \lim_{x \to +\infty} \frac{f(x)}{x} = \lim_{x \to +\infty} \frac{\frac{e^x}{x - 1}}{x}$$ $$m = \lim_{x \to +\infty} \frac{e^x}{x(x - 1)} = \lim_{x \to +\infty} \frac{e^x}{x^2 - x}$$Qui abbiamo un rapporto tra due funzioni che tendono a infinito. Ricordiamo che la funzione esponenziale \( e^x \) è un infinito di ordine superiore rispetto a qualsiasi potenza di \( x \), inclusa \( x^2 - x \).
Poiché il numeratore \( e^x \) cresce molto più velocemente del denominatore \( x^2 - x \) per \( x \to +\infty \), il rapporto tenderà a infinito:
$$m = \lim_{x \to +\infty} \frac{e^x}{x^2 - x} = +\infty$$Poiché il coefficiente angolare \( m \) tende a infinito (non è un valore finito e diverso da zero), questo significa che la funzione cresce molto più rapidamente di qualsiasi retta, e quindi **non possiede un asintoto obliquo** per \( x \to +\infty \).
Per \( \mathbf{x \to -\infty} \):
Come già stabilito, per \( x \to -\infty \), \( \lim_{x \to -\infty} f(x) = 0 \). Poiché la funzione tende a un asintoto orizzontale \( y=0 \), non può avere un asintoto obliquo per \( x \to -\infty \).
Per studiare la monotonia della funzione \( f(x) = \frac{e^x}{|x| - 1} \), calcoliamo la derivata prima considerando i due casi definiti dal valore assoluto.
Caso 1: \( x > 0 \) e \( x \neq 1 \)
\( f'(x) = \frac{e^x(x - 2)}{(x - 1)^2} \)
Caso 2: \( x < 0 \) e \( x \neq -1 \)
\( f'(x) = \frac{-xe^x}{(x + 1)^2} \)
La derivata prima è quindi: $$f'(x) = \begin{cases} \frac{e^x(x - 2)}{(x - 1)^2} & \text{se } x > 0, x \neq 1 \\ \frac{-xe^x}{(x + 1)^2} & \text{se } x < 0, x \neq -1 \end{cases}$$
La derivata prima non è definita in \( x = -1 \) e \( x = 1 \).
Analizziamo i limiti destro e sinistro della derivata in \( x = 0 \):
Poiché i limiti destro e sinistro della derivata in \( x = 0 \) sono diversi, la funzione non è derivabile in \( x = 0 \), che è un punto angoloso.
| Intervallo | Segno di \( f'(x) \) | Monotonia |
|---|---|---|
| \( x < -1 \) | \( + \) | Crescente |
| \( -1 < x < 0 \) | \( + \) | Crescente |
| \( x = 0 \) | Non derivabile | Massimo locale (nonostante non derivabile) |
| \( 0 < x < 1 \) | \( - \) | Decrescente |
| \( 1 < x < 2 \) | \( - \) | Decrescente |
| \( x = 2 \) | \( 0 \) | Minimo locale |
| \( x > 2 \) | \( + \) | Crescente |
Studiamo la concavità della funzione analizzando il segno della derivata seconda. Di seguito riportiamo i calcoli dettagliati per entrambi i casi:
Derivata prima: \( f'(x) = \frac{e^x(x - 2)}{(x - 1)^2} \)
Per calcolare la derivata seconda, applichiamo la regola del quoziente a \( f'(x) \). Siano \( u = e^x(x - 2) \) e \( v = (x - 1)^2 \).
Le derivate di \( u \) e \( v \) sono:
Applicando la regola del quoziente: $$f''(x) = \frac{u'v - uv'}{v^2} = \frac{e^x(x - 1)(x - 1)^2 - e^x(x - 2) \cdot 2(x - 1)}{((x - 1)^2)^2}$$ $$f''(x) = \frac{e^x(x - 1)^3 - 2e^x(x - 2)(x - 1)}{(x - 1)^4}$$ $$f''(x) = \frac{e^x(x - 1)[(x - 1)^2 - 2(x - 2)]}{(x - 1)^4}$$ $$f''(x) = \frac{e^x(x - 1)(x^2 - 2x + 1 - 2x + 4)}{(x - 1)^4}$$ $$f''(x) = \frac{e^x(x^2 - 4x + 5)}{(x - 1)^3}$$
Derivata prima: \( f'(x) = \frac{-xe^x}{(x + 1)^2} \)
Per calcolare la derivata seconda, applichiamo la regola del quoziente a \( f'(x) \). Siano \( u = -xe^x \) e \( v = (x + 1)^2 \).
Le derivate di \( u \) e \( v \) sono:
Applicando la regola del quoziente: $$f''(x) = \frac{u'v - uv'}{v^2} = \frac{-e^x(1 + x)(x + 1)^2 - (-xe^x) \cdot 2(x + 1)}{((x + 1)^2)^2}$$ $$f''(x) = \frac{-e^x(1 + x)^3 + 2xe^x(x + 1)}{(x + 1)^4}$$ $$f''(x) = \frac{e^x(x + 1)[-(1 + x)^2 + 2x]}{(x + 1)^4}$$ $$f''(x) = \frac{e^x(x + 1)(-1 - 2x - x^2 + 2x)}{(x + 1)^4}$$ $$f''(x) = \frac{-e^x(x^2 + 1)}{(x + 1)^3}$$
| Intervallo | Segno di \( f''(x) \) | Concavità |
|---|---|---|
| \( x < -1 \) | \( + \) | Verso l'alto |
| \( -1 < x < 1 \) |
|
Verso il basso |
| \( x > 1 \) | \( + \) | Verso l'alto |
Non ci sono punti di flesso poiché la derivata seconda non si annulla mai e i punti \( x = -1 \) e \( x = 1 \) non appartengono al dominio della funzione.
Perché la funzione \( f(x) = \sqrt{|x - \sqrt{|x| - 1}|} \) sia definita nei numeri reali, l'argomento della radice quadrata deve essere non negativo e l'espressione interna alla radice più interna deve essere definita.
Condizioni:
Pertanto, il dominio della funzione è: \[ \boxed{D = (-\infty, -1] \cup [1, +\infty)} \]
Calcoliamo \( f(-x) \):
\( f(-x) = \sqrt{|-x - \sqrt{|-x| - 1}|} = \sqrt{|-x - \sqrt{|x| - 1}|} = \sqrt{|x + \sqrt{|x| - 1}|} \).
Poiché \( f(-x) \neq f(x) \) e \( f(-x) \neq -f(x) \), la funzione non è né pari né dispari.
Per trovare l'intersezione con l'asse y, dobbiamo calcolare \( f(0) \).
Ricordiamo il **dominio** della funzione \( D = (-\infty, -1] \cup [1, +\infty) \).
Poiché \( x = 0 \) non appartiene al dominio della funzione (non è compreso negli intervalli \( (-\infty, -1] \) o \( [1, +\infty) \)), la funzione non è definita in \( x = 0 \).
Pertanto, **non ci sono intersezioni con l'asse y**.
Per trovare le intersezioni con l'asse x, dobbiamo risolvere l'equazione \( f(x) = 0 \):
$$\sqrt{|x - \sqrt{|x| - 1}|} = 0$$Questa equazione è vera se e solo se l'argomento della radice esterna è zero:
$$|x - \sqrt{|x| - 1}| = 0$$Ciò accade se l'espressione all'interno del valore assoluto è zero:
$$x - \sqrt{|x| - 1} = 0$$ $$x = \sqrt{|x| - 1}$$Per risolvere questa equazione, dobbiamo analizzare i due casi del dominio della funzione, dove \(|x|\) assume forme diverse.
Caso 1: \( x \ge 1 \)
In questo intervallo, \( |x| = x \). L'equazione diventa:
$$x = \sqrt{x - 1}$$Affinché la radice sia definita, dobbiamo avere \( x - 1 \ge 0 \implies x \ge 1 \). Inoltre, poiché la radice quadrata restituisce un valore non negativo, dobbiamo avere \( x \ge 0 \). Entrambe le condizioni sono soddisfatte se partiamo dal caso \( x \ge 1 \).
Eleviamo al quadrato entrambi i membri per eliminare la radice:
$$x^2 = x - 1$$ $$x^2 - x + 1 = 0$$Calcoliamo il discriminante (\( \Delta \)) di questa equazione quadratica:
$$\Delta = (-1)^2 - 4(1)(1) = 1 - 4 = -3$$Poiché il discriminante è negativo (\( \Delta < 0 \)), l'equazione \( x^2 - x + 1 = 0 \) **non ha soluzioni reali**. Quindi, non ci sono intersezioni con l'asse x per \( x \ge 1 \).
Caso 2: \( x \le -1 \)
In questo intervallo, \( |x| = -x \). L'equazione diventa:
$$x = \sqrt{-x - 1}$$Affinché la radice sia definita, dobbiamo avere \( -x - 1 \ge 0 \implies -x \ge 1 \implies x \le -1 \). Questa condizione è coerente con il caso \( x \le -1 \).
Tuttavia, osserviamo che il membro sinistro dell'equazione \( x \) è un numero negativo (poiché \( x \le -1 \)), mentre il membro destro \( \sqrt{-x - 1} \) è, per definizione, sempre un numero non negativo (maggiore o uguale a zero).
Un numero negativo non può essere uguale a un numero non negativo.
Pertanto, l'equazione \( x = \sqrt{-x - 1} \) **non ha soluzioni reali** per \( x \le -1 \).
In conclusione, poiché non sono state trovate soluzioni reali in nessuno dei due casi considerati, **non ci sono intersezioni con l'asse x**.
La funzione \( f(x) = \sqrt{|x - \sqrt{|x| - 1}|} \) è definita come la radice quadrata di un valore assoluto. Un valore assoluto è sempre non negativo, e la radice quadrata di un numero non negativo è anch'essa non negativa.
Pertanto, \( f(x) \ge 0 \) per tutti gli \( x \) nel dominio \( (-\infty, -1] \cup [1, +\infty) \).
\( \lim_{x \to +\infty} \sqrt{|x - \sqrt{|x| - 1}|} = \lim_{x \to +\infty} \sqrt{x - \sqrt{x - 1}} \)
Come si vede razionalizzando, l'espressione interna si comporta come \( \frac{x^2 - x + 1}{x + \sqrt{x - 1}} \).
Per grandi valori di \( x \), i termini dominanti sono \( x^2 \) al numeratore e \( x \) al denominatore. Quindi, l'espressione interna è asintotica a \( \frac{x^2}{x} = x \).
Pertanto, \( \lim_{x \to +\infty} \sqrt{x - \sqrt{x - 1}} = \lim_{x \to +\infty} \sqrt{x} = +\infty \).
Quando \( x \to -\infty \), abbiamo \( |x| = -x \). La funzione diventa:
$$f(x) = \sqrt{|x - \sqrt{-x - 1}|}$$Consideriamo l'argomento del valore assoluto: \( x - \sqrt{-x - 1} \).
Per \( x \to -\infty \), \( x \to -\infty \) e \( \sqrt{-x - 1} \to +\infty \). Quindi l'espressione \( x - \sqrt{-x - 1} \) si presenta nella forma \( -\infty - (\text{un infinito positivo, che mantiene il segno negativo}) \), risultando \( -\infty \).
Poiché l'espressione interna al valore assoluto tende a \( -\infty \), il valore assoluto di tale espressione tende a \( |-\infty| = +\infty \).
Infine, la radice quadrata di un valore che tende a \( +\infty \) è \( +\infty \).
$$\lim_{x \to -\infty} \sqrt{|x - \sqrt{|x| - 1}|} = +\infty$$\( f(-1) = \sqrt{|-1 - \sqrt{|-1| - 1}|} = 1 \)
Dall'analisi dei limiti a \( \pm \infty \), non ci sono asintoti orizzontali finiti.
Per gli asintoti obliqui, \( \lim_{x \to \pm \infty} \frac{f(x)}{x} = 0 \), perché il denominatore è infinito di ordine superiore rispetto al numeratore, quindi non ci sono asintoti obliqui.
Non ci sono asintoti verticali poiché la funzione è definita e continua agli estremi finiti del dominio.
Per calcolare la derivata prima, dobbiamo considerare il dominio \( D = (-\infty, -1] \cup [1, +\infty) \) e distinguere due casi a seconda del segno di \( x \).
In questo intervallo, \( |x| = x \). La funzione diventa \( f(x) = \sqrt{|x - \sqrt{x - 1}|} \).
Come abbiamo visto nelle intersezioni con gli assi, \( x - \sqrt{x - 1} = x^2 - x + 1 \) quando elevato al quadrato. Il discriminante di \( x^2 - x + 1 \) è negativo (\( -3 \)), il che significa che \( x^2 - x + 1 \) è sempre positivo (poiché il coefficiente di \( x^2 \) è positivo).
Questo implica che \( x - \sqrt{x - 1} \) è sempre positivo per \( x > 1 \). Quindi, \( |x - \sqrt{x - 1}| = x - \sqrt{x - 1} \).
La funzione da derivare diventa \( f(x) = \sqrt{x - \sqrt{x - 1}} \).
Usiamo la regola della catena: \( \frac{d}{dx}(\sqrt{u}) = \frac{1}{2\sqrt{u}} \cdot u' \).
Sia \( u = x - \sqrt{x - 1} \). Allora \( u' = \frac{d}{dx}(x - \sqrt{x - 1}) = 1 - \frac{1}{2\sqrt{x - 1}} \).
Quindi, per \( x > 1 \):
$$f'(x) = \frac{1}{2\sqrt{x - \sqrt{x - 1}}} \cdot \left(1 - \frac{1}{2\sqrt{x - 1}}\right)$$ $$f'(x) = \frac{1}{2\sqrt{x - \sqrt{x - 1}}} \cdot \frac{2\sqrt{x - 1} - 1}{2\sqrt{x - 1}}$$ $$f'(x) = \frac{2\sqrt{x - 1} - 1}{4\sqrt{x - \sqrt{x - 1}}\sqrt{x - 1}}$$In questo intervallo, \( |x| = -x \). La funzione diventa \( f(x) = \sqrt{|x - \sqrt{-x - 1}|} \).
Come analizzato nei limiti per \( x \to -\infty \) e nelle intersezioni, per \( x < -1 \), il termine \( x - \sqrt{-x - 1} \) è sempre negativo.
Quindi, \( |x - \sqrt{-x - 1}| = -(x - \sqrt{-x - 1}) = -x + \sqrt{-x - 1} \).
La funzione da derivare diventa \( f(x) = \sqrt{-x + \sqrt{-x - 1}} \).
Usiamo la regola della catena: \( \frac{d}{dx}(\sqrt{u}) = \frac{1}{2\sqrt{u}} \cdot u' \).
Sia \( u = -x + \sqrt{-x - 1} \). Allora \( u' = \frac{d}{dx}(-x + \sqrt{-x - 1}) = -1 + \frac{1}{2\sqrt{-x - 1}} \cdot (-1) = -1 - \frac{1}{2\sqrt{-x - 1}} \).
Quindi, per \( x < -1 \):
$$f'(x) = \frac{1}{2\sqrt{-x + \sqrt{-x - 1}}} \cdot \left(-1 - \frac{1}{2\sqrt{-x - 1}}\right)$$ $$f'(x) = \frac{1}{2\sqrt{-x + \sqrt{-x - 1}}} \cdot \frac{-2\sqrt{-x - 1} - 1}{2\sqrt{-x - 1}}$$ $$f'(x) = \frac{-2\sqrt{-x - 1} - 1}{4\sqrt{-x + \sqrt{-x - 1}}\sqrt{-x - 1}}$$Analizziamo il segno di \( f'(x) \) in base ai due casi considerati.
Per \( x > 1 \):
$$f'(x) = \frac{2\sqrt{x - 1} - 1}{4\sqrt{x - \sqrt{x - 1}}\sqrt{x - 1}}$$Il denominatore è sempre positivo (prodotto di radici quadrate). Il segno di \( f'(x) \) dipende solo dal numeratore \( 2\sqrt{x - 1} - 1 \).
Poniamo il numeratore maggiore di zero:
$$2\sqrt{x - 1} - 1 > 0$$ $$2\sqrt{x - 1} > 1$$ $$\sqrt{x - 1} > \frac{1}{2}$$Eleviamo al quadrato entrambi i membri (sono entrambi positivi):
$$x - 1 > \frac{1}{4}$$ $$x > 1 + \frac{1}{4}$$ $$x > \frac{5}{4}$$Quindi, per \( \mathbf{x > \frac{5}{4}} \), la derivata \( f'(x) > 0 \) e la funzione è **crescente**.
Per \( \mathbf{1 < x < \frac{5}{4}} \), la derivata \( f'(x) < 0 \) e la funzione è **decrescente**.
In \( x = \frac{5}{4} \), \( f'(x) = 0 \). Questo è un punto di minimo locale. Calcoliamo \( f(\frac{5}{4}) = \sqrt{|\frac{5}{4} - \sqrt{\frac{5}{4} - 1}|} = \sqrt{|\frac{5}{4} - \sqrt{\frac{1}{4}}|} = \sqrt{|\frac{5}{4} - \frac{1}{2}|} = \sqrt{|\frac{5-2}{4}|} = \sqrt{\frac{3}{4}} = \frac{\sqrt{3}}{2} \). Il punto di minimo locale è \( \left(\frac{5}{4}, \frac{\sqrt{3}}{2}\right) \).
Per \( x < -1 \):
$$f'(x) = \frac{-2\sqrt{-x - 1} - 1}{4\sqrt{-x + \sqrt{-x - 1}}\sqrt{-x - 1}}$$Il denominatore è sempre positivo (prodotto di radici quadrate).
Il numeratore \( -2\sqrt{-x - 1} - 1 \) è sempre negativo, poiché \( \sqrt{-x - 1} \) è sempre positivo (o nullo per \( x=-1 \)), quindi \( -2\sqrt{-x - 1} \) è sempre negativo, e sottraendo 1 rimane negativo.
Pertanto, per \( \mathbf{x < -1} \), la derivata \( f'(x) < 0 \) e la funzione è **decrescente**.
In sintesi, la funzione è **decrescente per \( x < -1 \)** e per \( \mathbf{1 < x < \frac{5}{4}} \), mentre è **crescente per \( x > \frac{5}{4} \)}.
| Intervallo | Segno di \( f'(x) \) | Monotonia |
|---|---|---|
| \( x < -1 \) | \( - \) | Decrescente |
| \( x = -1 \) | Non derivabile (tangente verticale) | |
| \( -1 < x < 1 \) | Non nel dominio | |
| \( x = 1 \) | Non derivabile (tangente verticale) | |
| \( 1 < x < \frac{5}{4} \) | \( - \) | Decrescente |
| \( x = \frac{5}{4} \) | \( 0 \) | Minimo locale |
| \( x > \frac{5}{4} \) | \( + \) | Crescente |
Analizziamo il comportamento della derivata prima nei punti di bordo del dominio in cui la funzione è definita.
Quando \( x \to 1^+ \), usiamo la derivata del Caso 1 (\( x > 1 \)):
$$f'(x) = \frac{2\sqrt{x - 1} - 1}{4\sqrt{x - \sqrt{x - 1}}\sqrt{x - 1}}$$Analizziamo il numeratore e il denominatore separatamente per \( x \to 1^+ \):
Pertanto:
$$ \lim_{x \to 1^+} f'(x) = \frac{-1}{0^+} = -\infty $$Questo risultato indica che la pendenza della retta tangente al grafico della funzione tende a \( -\infty \) avvicinandosi a \( x = 1 \) da destra. Una pendenza infinita (in valore assoluto) corrisponde a una **tangente verticale** nel punto \( (1, f(1)) = (1, 0) \). Il segno negativo indica che la tangente "punta" verso il basso.
Quando \( x \to -1^- \), usiamo la derivata del Caso 2 (\( x < -1 \)):
$$f'(x) = \frac{-2\sqrt{-x - 1} - 1}{4\sqrt{-x + \sqrt{-x - 1}}\sqrt{-x - 1}}$$Analizziamo il numeratore e il denominatore separatamente per \( x \to -1^- \):
Pertanto:
$$ \lim_{x \to -1^-} f'(x) = \frac{-1}{0^+} = -\infty $$Analogamente al caso precedente, questo risultato indica che la pendenza della retta tangente al grafico della funzione tende a \( -\infty \) avvicinandosi a \( x = -1 \) da sinistra. Si ha una **tangente verticale** nel punto \( (-1, f(-1)) = (-1, 0) \). Il segno negativo indica che la tangente "punta" verso il basso.
Tralasciamo lo studio della derivata seconda, che risulta particolarmente laborioso.