



Studia la funzione e controlla la soluzione guidata dei vari punti cliccando sul bottone corrispondente. Premi il bottone RIPRISTINA per cancellare gli output.
\( x \in \mathbb{R} \) → \( (-\infty, +\infty) \)
Se \( x = 0 \), \( y = (4(0) - 2) e^{2(0)} = -2 \cdot 1 = -2 \). Punto di intersezione con l'asse y: \( (0, -2) \).
Se \( y = 0 \), \( (4x - 2) e^{2x} = 0 \). Poiché \( e^{2x} \) non è mai nullo, dobbiamo risolvere \( 4x - 2 = 0 \), da cui \( x = \frac{2}{4} = \frac{1}{2} \). Punto di intersezione con l'asse x: \( (\frac{1}{2}, 0) \).
La funzione è positiva se \( 4x - 2 > 0 \), ovvero \( x > \frac{1}{2} \), poiché \( e^{2x} \) è sempre positivo.
\( \lim_{x \to +\infty} (4x - 2) e^{2x} = [(+\infty) \cdot (+\infty)] = +\infty \).
\( \lim_{x \to -\infty} (4x - 2) e^{2x} \). Si ricordi il limite notevole \( \lim_{t \to -\infty} t e^{at} = 0^- \) per \( a > 0 \). Quindi, \( \lim_{x \to -\infty} (4x - 2) e^{2x} = 0^- \).
Asintoto orizzontale per \( x \to -\infty \): \( y = 0 \) poiché \( \lim_{x \to -\infty} (4x - 2) e^{2x} = 0 \).
Non c’è asintoto obliquo perché la funzione, per x che tende a più infinito, si comporta come \( 4x e^{2x} \), che non è un infinito del primo ordine (cresce più rapidamente di \( mx + q \)).
\( f'(x) = \frac{d}{dx} [(4x - 2) e^{2x}] = 4 \cdot e^{2x} + (4x - 2) \cdot 2 e^{2x} = e^{2x} (4 + 8x - 4) = e^{2x} (8x) = 8x e^{2x} \).
\( f'(x) = 8x e^{2x} \): quindi la funzione è crescente se \( x > 0 \) e decrescente se \( x < 0 \); \( x = 0 \) è quindi punto di minimo relativo (e assoluto), con ordinata \( f(0) = -2 \).
La funzione ammette quindi un unico punto di minimo m, con coordinate \( (0, -2) \).
\( f''(x) = \frac{d}{dx} [8x e^{2x}] = 8 \cdot e^{2x} + 8x \cdot 2 e^{2x} = e^{2x} (8 + 16x) = 8 e^{2x} (1 + 2x) \).
\( f''(x) = 8 e^{2x} (1 + 2x) \): quindi il grafico di f volge la concavità verso l’alto se \( 1 + 2x > 0 \), cioè \( x > -\frac{1}{2} \), e verso il basso se \( x < -\frac{1}{2} \): \( x = -\frac{1}{2} \) è quindi l’unico punto di flesso, con ordinata \( f(-\frac{1}{2}) = (4(-\frac{1}{2}) - 2) e^{2(-\frac{1}{2})} = (-2 - 2) e^{-1} = -4e^{-1} = -\frac{4}{e} \).
La funzione ammette un unico flesso F, di coordinate \( (-\frac{1}{2}, -\frac{4}{e}) \).
\( x \in \mathbb{R} \setminus \{\frac{1}{2}\} \) → \( (-\infty, \frac{1}{2}) \cup (\frac{1}{2}, +\infty) \)
\( f(-x) = \frac{e^{-x}}{-2x - 1} \). Non è né pari né dispari.
Asse y (x=0): \( y = \frac{e^0}{-1} = -1 \) → Punto (0, -1)
Asse x (y=0): \( e^x = 0 \) (mai verificato), quindi non ci sono intersezioni con l'asse x.
Il segno di \( f(x) \) dipende dal segno di \( 2x - 1 \) poiché \( e^x \) è sempre positivo.
Utilizzando la regola del quoziente: \( f'(x) = \frac{e^x(2x - 1) - e^x(2)}{(2x - 1)^2} = \frac{e^x(2x - 1 - 2)}{(2x - 1)^2} = \frac{e^x(2x - 3)}{(2x - 1)^2} \)
\[ f''(x) = \frac{d}{dx} \left( \frac{e^x(2x - 3)}{(2x - 1)^2} \right) = \frac{[e^x(2x - 3) + e^x(2)](2x - 1)^2 - e^x(2x - 3) \cdot 2(2x - 1)(2)}{(2x - 1)^4} \]
\[ = \frac{e^x(2x - 1)(2x - 1) - 4e^x(2x - 3)}{(2x - 1)^3} = \frac{e^x(4x^2 - 4x + 1 - 8x + 12)}{(2x - 1)^3} = \frac{e^x(4x^2 - 12x + 13)}{(2x - 1)^3} \]
(si trascuri lo studio della derivata seconda)
La funzione è definita per tutti i \( x \in \mathbb{R} \) tali che \( x \neq 0 \) e \( e^{1/x} - 1 \neq 0 \). \( e^{1/x} - 1 = 0 \) quando \( e^{1/x} = 1 \), ovvero \( 1/x = 0 \), che non ha soluzione. Quindi il dominio è \( x \in \mathbb{R} \setminus \{0\} \) → \( (-\infty, 0) \cup (0, +\infty) \)
\( f(-x) = \frac{1}{(e^{-1/x} - 1)^2} = \frac{1}{(\frac{1}{e^{1/x}} - 1)^2} = \frac{1}{(\frac{1 - e^{1/x}}{e^{1/x}})^2} = \frac{(e^{1/x})^2}{(1 - e^{1/x})^2} = \frac{e^{2/x}}{(e^{1/x} - 1)^2} \). Non è né pari né dispari.
Asse y (x=0): \( x = 0 \) non è nel dominio, quindi non ci sono intersezioni con l'asse y.
Asse x (y=0): \( \frac{1}{(e^{1/x} - 1)^2} = 0 \) non ha soluzioni, quindi non ci sono intersezioni con l'asse x.
Poiché il numeratore è \( 1 \) (positivo) e il denominatore \( (e^{1/x} - 1)^2 \) è sempre non negativo (ed è definito per \( x \neq 0 \)), la funzione è sempre positiva sul suo dominio.
non ci sono asintoti verticali.
\[ f(x) = \frac{1}{(e^{1/x} - 1)^2} = (e^{1/x} - 1)^{-2} \]
Utilizziamo il teorema: \( \frac{d}{dx}([g(x)]^{\alpha}) = \alpha \cdot [g(x)]^{\alpha - 1} \cdot g'(x) \), dove nel nostro caso \( g(x) = e^{1/x} - 1 \) e \( \alpha = -2 \).
\( \alpha = -2 \)
\( g(x) = e^{1/x} - 1 \)
Dobbiamo trovare la derivata di \( g(x) = e^{1/x} - 1 \). La derivata di \( -1 \) è \( 0 \). Per la derivata di \( e^{1/x} \), applichiamo nuovamente la regola della catena con \( h(x) = 1/x \).
\( \frac{d}{dx}[e^{h(x)}] = e^{h(x)} \cdot h'(x) \)
\( h(x) = \frac{1}{x} = x^{-1} \), quindi \( h'(x) = -1 \cdot x^{-2} = -\frac{1}{x^2} \).
Pertanto, \( \frac{d}{dx}[e^{1/x}] = e^{1/x} \cdot (-\frac{1}{x^2}) = -\frac{e^{1/x}}{x^2} \).
La derivata di \( g(x) \) è quindi: \( g'(x) = \frac{d}{dx}[e^{1/x} - 1] = -\frac{e^{1/x}}{x^2} - 0 = -\frac{e^{1/x}}{x^2} \).
Ora sostituiamo i valori nella formula: \( f'(x) = \alpha \cdot [g(x)]^{\alpha - 1} \cdot g'(x) \)
\[ f'(x) = -2 \cdot (e^{1/x} - 1)^{-2 - 1} \cdot \left( -\frac{e^{1/x}}{x^2} \right) \]
\[ f'(x) = -2 \cdot (e^{1/x} - 1)^{-3} \cdot \left( -\frac{e^{1/x}}{x^2} \right) \]
\[ f'(x) = \frac{2e^{1/x}}{x^2(e^{1/x} - 1)^3} \]
Non ci sono punti critici nel dominio della derivata prima.
Il calcolo della derivata seconda è piuttosto complesso e non verrà riportato qui per brevità.
La funzione \( f(x) = 2^x - x^2 \) è definita per ogni \( x \in \mathbb{R} \) poiché sia la funzione esponenziale \( 2^x \) che la funzione polinomiale \( x^2 \) sono definite su tutto l'insieme dei numeri reali.
\[ \boxed{D = \mathbb{R}} \]
Calcoliamo \( f(-x) \):
\[ f(-x) = 2^{-x} - (-x)^2 = \frac{1}{2^x} - x^2 \]
Poiché \( f(-x) \neq f(x) \) e \( f(-x) \neq -f(x) \), la funzione non è né pari né dispari.
Asse x (y=0):
\[ 2^x - x^2 = 0 \implies 2^x = x^2 \]
Questa equazione non ha soluzioni algebriche semplici. Per analizzare le soluzioni, rappresentiamo nello stesso sistema di riferimento le funzioni \( a(x) = 2^x \) (in rosso) e \( b(x) = x^2 \) (in blu).
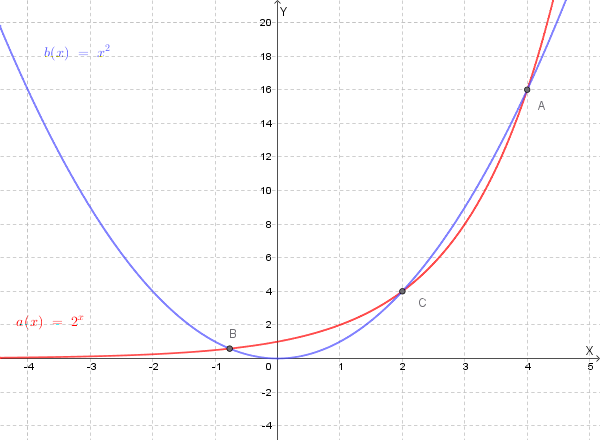
Osservando il grafico, possiamo notare che ci sono tre punti di intersezione, che corrispondono alle soluzioni dell'equazione \( 2^x = x^2 \):
Punti di intersezione approssimativi con l'asse x: \( (-0.7667, 0) \), \( (2, 0) \), \( (4, 0) \).
Asse y (x=0):
\[ f(0) = 2^0 - 0^2 = 1 - 0 = 1 \implies (0, 1) \]
Il segno della funzione \( f(x) = 2^x - x^2 \) può essere dedotto dal seguente grafico, che mostra le funzioni \( a(x) = 2^x \) (in rosso) e \( b(x) = x^2 \) (in blu).

La funzione \( f(x) = 2^x - x^2 \) è positiva dove il grafico di \( 2^x \) è sopra il grafico di \( x^2 \), negativa dove è sotto, e nulla nei punti di intersezione.
| Intervallo | \( 2^x > x^2 \) | Segno di \( f(x) = 2^x - x^2 \) |
|---|---|---|
| \( x < -0.7667 \) | No | Negativo |
| \( -0.7667 < x < 2 \) | Sì | Positivo |
| \( 2 < x < 4 \) | No | Negativo |
| \( x > 4 \) | Sì | Positivo |
In sintesi:
Per \( x \to +\infty \):
\[ \lim_{x \to +\infty} (2^x - x^2) = +\infty - \infty \]
Per risolvere questa forma indeterminata, notiamo che la funzione esponenziale cresce più velocemente di qualsiasi funzione polinomiale:
\[ \lim_{x \to +\infty} (2^x - x^2) = +\infty \]
Per \( x \to -\infty \):
\[ \lim_{x \to -\infty} (2^x - x^2) = 0 - (-\infty)^2 = 0 - (+\infty) = -\infty \]
\[ \lim_{x \to +\infty} \frac{2^x - x^2}{x} = \lim_{x \to +\infty} \left( \frac{2^x}{x} \right) = +\infty \]
\[ \lim_{x \to -\infty} \frac{2^x - x^2}{x} = \lim_{x \to -\infty} \left( \frac{2^x}{x} - x \right) = 0 - (-\infty) = +\infty \]
Poiché il limite di \( m \) non è finito, non ci sono asintoti obliqui.\[ f'(x) = 2^x \ln(2) - 2x \]
Per studiare il segno della derivata prima facciamo uno studio grafico, rappresentando nello stesso sistema di riferimento le funzioni \( c(x) = 2^x \ln(2) \) (in blu) e \( d(x) = 2x \) (in verde).
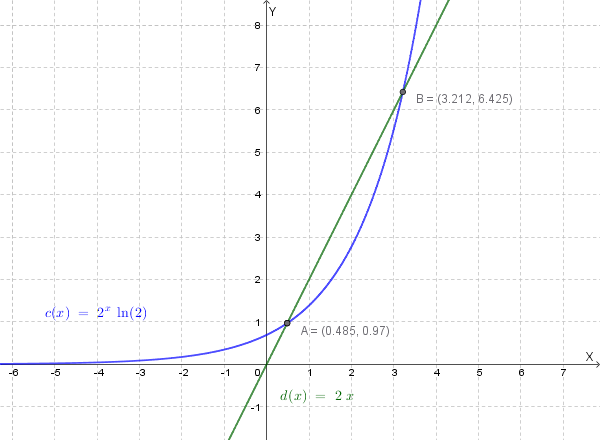
Dal grafico possiamo dedurre che la derivata prima si annulla in due punti: uno tra \( 0 \) e \( 1 \) (che vale circa \( 0.5 \)) ed uno tra \( 3 \) e \( 4 \) (che vale circa \( 3.2 \)).
Quindi abbiamo la seguente tabella dei segni della derivata prima:
| Intervallo | \( 2^x \ln(2) > 2x \) | Segno di \( f'(x) \) | Monotonia di \( f(x) \) |
|---|---|---|---|
| \( x < 0.5 \) | Sì | Positivo | Crescente |
| \( 0.5 < x < 3.2 \) | No | Negativo | Decrescente |
| \( x > 3.2 \) | Sì | Positivo | Crescente |
Punto di massimo locale approssimativo in \( x \approx 0.5 \).
Punto di minimo locale approssimativo in \( x \approx 3.2 \).
\[ f''(x) = \frac{d}{dx} (2^x \ln(2) - 2x) = 2^x (\ln(2))^2 - 2 \]
Per trovare i punti di flesso, risolviamo \( f''(x) = 0 \):
\[ 2^x (\ln(2))^2 - 2 = 0 \implies 2^x = \frac{2}{(\ln(2))^2} \]
\[ x \ln(2) = \ln\left(\frac{2}{(\ln(2))^2}\right) = \ln(2) - 2\ln(\ln(2)) \]
\[ x = 1 - \frac{2\ln(\ln(2))}{\ln(2)} \approx 1 - \frac{2(-0.3665)}{0.6931} \approx 1 + 1.057 \approx 2.057 \]
Punto di flesso approssimativo in \( x \approx 2.057 \).