



Studia la funzione e controlla la soluzione guidata dei vari punti cliccando sul bottone corrispondente. Premi il bottone RIPRISTINA per cancellare gli output.
N.B. la funzione ha periodo \( \pi \), quindi possiamo limitare lo studio all’intervallo \( [0, \pi] \).
\( x \neq \frac{\pi}{2} \) → \( [0, \frac{\pi}{2}) \cup (\frac{\pi}{2}, \pi] \).
Visto il dominio, la funzione non può essere né pari né dispari.
\( \tan x (\frac{1}{3} \tan^2 x + \tan x + 1) > 0 \) se \( \tan x > 0 \): \( 0 < x < \frac{\pi}{2} \), perché il secondo fattore del prodotto è sempre positivo.
\( x = \frac{\pi}{2} \) è un asintoto verticale.
Non ci sono asintoti orizzontali né obliqui poiché la funzione è definita in un intervallo limitato e presenta un asintoto verticale.
\( f'(x) = \frac{d}{dx} (\frac{1}{3} \tan^3 x + \tan^2 x + \tan x) = \tan^2 x \cdot \frac{1}{\cos^2 x} + 2 \tan x \cdot \frac{1}{\cos^2 x} + \frac{1}{\cos^2 x} = \frac{\tan^2 x + 2 \tan x + 1}{\cos^2 x} = \frac{(\tan x + 1)^2}{\cos^2 x} = (\tan x + 1)^2 \cos^{-2} x \).
Nel dominio della funzione risulta \( f'(x) = 0 \) quando \( \tan x + 1 = 0 \) ⟹ \( \tan x = -1 \), quindi per \( x = \frac{3}{4} \pi \) (punto di flesso a tangente orizzontale); \( f(\frac{3}{4} \pi) = \frac{1}{3} (-1)^3 + (-1)^2 + (-1) = -\frac{1}{3} \).
Flesso \( F = (\frac{3}{4} \pi, -\frac{1}{3}) \).
\( f'(x) = (\tan x + 1)^2 \cos^{-2} x > 0 \) per \( \forall x \neq \frac{3}{4} \pi \): la funzione è sempre crescente.
La derivata prima è \( f'(x) = (\tan x + 1)^2 \sec^2 x \).
La derivata seconda è \( f''(x) = 2(\tan x + 1)(\tan^2 x + 1)(2\tan^2 x + \tan x + 1) \).
Il segno di \( f''(x) \) dipende dal segno di \( \tan x + 1 \), poiché \( \tan^2 x + 1 > 0 \) e \( 2\tan^2 x + \tan x + 1 > 0 \) nel dominio.
\( \tan x + 1 > 0 \) per \( 0 \le x < \frac{\pi}{2} \) e \( \frac{3}{4} \pi < x \le \pi \).
\( \tan x + 1 < 0 \) per \( \frac{\pi}{2} < x < \frac{3}{4} \pi \).
\( \tan x + 1 = 0 \) per \( x = \frac{3}{4} \pi \) (punto di flesso).
| Intervallo | \( \tan x + 1 \) | \( f''(x) \) | Concavità |
|---|---|---|---|
| \( 0 \le x < \frac{\pi}{2} \) | \( > 0 \) | \( > 0 \) | Verso l'alto |
| \( \frac{\pi}{2} < x < \frac{3}{4} \pi \) | \( < 0 \) | \( < 0 \) | Verso il basso |
| \( x = \frac{3}{4} \pi \) | \( = 0 \) | \( = 0 \) | Punto di flesso |
| \( \frac{3}{4} \pi < x \le \pi \) | \( > 0 \) | \( > 0 \) | Verso l'alto |
La funzione ha periodo \( T = 2\pi \). È quindi sufficiente studiarla nell'intervallo \( 0 \le x \le 2\pi \).
La funzione, nell’intervallo di studio, è definita quando \( 1 + \sin(x) \neq 0 \), ovvero \( \sin(x) \neq -1 \). Questo si verifica per \( x \neq \frac{3}{2}\pi \).
Dominio: \( [0, \frac{3}{2}\pi) \cup (\frac{3}{2}\pi, 2\pi] \).
Visto il dominio di studio \( [0, \frac{3}{2}\pi) \cup (\frac{3}{2}\pi, 2\pi] \), che non è simmetrico rispetto all'origine, la funzione non può essere né pari né dispari.
Essendo il denominatore \( 1 + \sin(x) \) sempre non negativo (e diverso da zero nel dominio), la funzione è positiva quando \( \cos(x) > 0 \). Questo si verifica per \( 0 \le x < \frac{\pi}{2} \) e \( \frac{3}{2}\pi < x \le 2\pi \).
\( f'(x) = \frac{-\sin(x)(1+\sin(x)) - \cos(x)(\cos(x))}{(1+\sin(x))^2} = \frac{-\sin(x) - \sin^2(x) - \cos^2(x)}{(1+\sin(x))^2} = \frac{-\sin(x) - 1}{(1+\sin(x))^2} = -\frac{1}{1+\sin(x)} \).
Pertanto la funzione è sempre decrescente poiché \( 1 + \sin(x) > 0 \) nel dominio, e la derivata prima non si annulla mai.
\( f''(x) = \frac{d}{dx} \left( -(1+\sin(x))^{-1} \right) = -(-1)(1+\sin(x))^{-2} (\cos(x)) = \frac{\cos(x)}{(1+\sin(x))^2} \).
Il grafico ha quindi la concavità verso l’alto se \( \cos(x) > 0 \) per \( 0 \le x < \frac{\pi}{2} \) e \( \frac{3}{2}\pi < x \le 2\pi \), e la concavità verso il basso se \( \cos(x) < 0 \) per \( \frac{\pi}{2} < x < \frac{3}{2}\pi \).
Si ha un flesso per \( \cos(x) = 0 \), ovvero \( x = \frac{\pi}{2} \), con ordinata \( f(\frac{\pi}{2}) = \frac{\cos(\frac{\pi}{2})}{1+\sin(\frac{\pi}{2})} = \frac{0}{1+1} = 0 \). Flesso in \( (\frac{\pi}{2}, 0) \).
La funzione \( f(x) = \sin(x) + \frac{1}{3}\sin(3x) \) è definita, continua e derivabile su tutto R. Dobbiamo studiarla nell'intervallo \( [-\pi, \pi] \).
La funzione \( \sin(x) \) ha periodo \( 2\pi \), la funzione \( \sin(3x) \) ha periodo \( \frac{2\pi}{3} \). La funzione \( f(x) \) ha come periodo il minimo comune multiplo fra \( 2\pi \) e \( \frac{2\pi}{3} \), che è \( 2\pi \).
Studiamo la parità o disparità della funzione calcolando \( f(-x) \):
\( f(-x) = \sin(-x) + \frac{1}{3}\sin(3(-x)) = -\sin(x) - \frac{1}{3}\sin(3x) = -(\sin(x) + \frac{1}{3}\sin(3x)) = -f(x) \).
Poiché \( f(-x) = -f(x) \), la funzione \( f(x) = \sin(x) + \frac{1}{3}\sin(3x) \) è una **funzione dispari**. Il suo grafico è simmetrico rispetto all'origine degli assi cartesiani.
Valutando \( f(0) = \sin(0) + \frac{1}{3}\sin(0) = 0 \). Il punto di intersezione con l'asse y è \( (0, 0) \).
Risolviamo l'equazione \( \sin(x) + \frac{1}{3}\sin(3x) = 0 \). Per fare ciò, utilizziamo la formula per \( \sin(3x) \).
Derivazione della formula di \( \sin(3x) \):
\( \sin(3x) = \sin(2x + x) = \sin(2x)\cos(x) + \cos(2x)\sin(x) \)
Usando \( \sin(2x) = 2\sin(x)\cos(x) \) e \( \cos(2x) = \cos^2(x) - \sin^2(x) \):
\( \sin(3x) = (2\sin(x)\cos(x))\cos(x) + (\cos^2(x) - \sin^2(x))\sin(x) \)
\( \sin(3x) = 2\sin(x)\cos^2(x) + \sin(x)\cos^2(x) - \sin^3(x) \)
Usando \( \cos^2(x) = 1 - \sin^2(x) \):
\( \sin(3x) = 2\sin(x)(1 - \sin^2(x)) + \sin(x)(1 - \sin^2(x)) - \sin^3(x) = 3\sin(x) - 4\sin^3(x) \)
Sostituendo nella nostra equazione \( \sin(x) + \frac{1}{3}(3\sin(x) - 4\sin^3(x)) = 0 \), otteniamo:
\( 2\sin(x) - \frac{4}{3}\sin^3(x) = 0 \)
\( 2\sin(x) \left( 1 - \frac{2}{3}\sin^2(x) \right) = 0 \)
Questo implica \( \sin(x) = 0 \) o \( \sin^2(x) = \frac{3}{2} \).
Le intersezioni con l'asse x sono quindi nei punti \( (-\pi, 0), (0, 0), (\pi, 0) \).
Il segno di \( f(x) = \sin(x) + \frac{1}{3}\sin(3x) \) è determinato analizzando il segno della sua forma fattorizzata: \( f(x) = 2\sin(x) \left( 1 - \frac{2}{3}\sin^2(x) \right) \).
Poiché il fattore \( \left( 1 - \frac{2}{3}\sin^2(x) \right) \) è sempre non negativo nell'intervallo \( [-\pi, \pi] \), il segno di \( f(x) \) dipende unicamente dal segno di \( \sin(x) \).
| Intervallo | \( \sin(x) \) | \( f(x) \) |
|---|---|---|
| \( -\pi < x < 0 \) | \( < 0 \) | \( < 0 \) |
| \( x = -\pi, 0, \pi \) | \( = 0 \) | \( = 0 \) |
| \( 0 < x < \pi \) | \( > 0 \) | \( > 0 \) |
Dato che la funzione \( f(x) = \sin(x) + \frac{1}{3}\sin(3x) \) è continua nell'intervallo chiuso \( [-\pi, \pi] \), non ci sono limiti da calcolare all'interno dell'intervallo. Tuttavia, possiamo valutare la funzione agli estremi:
Dato che la funzione è continua in un intervallo chiuso, non ci sono asintoti.
La derivata prima di \( f(x) = \sin(x) + \frac{1}{3}\sin(3x) \) è \( f'(x) = \cos(x) + \cos(3x) \).
Derivazione della formula di \( \cos(3x) \):
\( \cos(3x) = \cos(2x + x) = \cos(2x)\cos(x) - \sin(2x)\sin(x) \)
Usando \( \sin(2x) = 2\sin(x)\cos(x) \) e \( \cos(2x) = \cos^2(x) - \sin^2(x) \):
\( \cos(3x) = (\cos^2(x) - \sin^2(x))\cos(x) - (2\sin(x)\cos(x))\sin(x) \)
\( \cos(3x) = \cos^3(x) - \sin^2(x)\cos(x) - 2\sin^2(x)\cos(x) \)
\( \cos(3x) = \cos^3(x) - 3\sin^2(x)\cos(x) \)
Usando \( \sin^2(x) = 1 - \cos^2(x) \):
\( \cos(3x) = \cos^3(x) - 3(1 - \cos^2(x))\cos(x) = \cos^3(x) - 3\cos(x) + 3\cos^3(x) = 4\cos^3(x) - 3\cos(x) \)
Quindi, \( f'(x) = \cos(x) + (4\cos^3(x) - 3\cos(x)) = 4\cos^3(x) - 2\cos(x) = 2\cos(x)(2\cos^2(x) - 1) \).
Imponendo \( f'(x) = 0 \), otteniamo \( \cos(x) = 0 \) o \( \cos^2(x) = \frac{1}{2} \). Le soluzioni nell'intervallo \( [-\pi, \pi] \) sono \( x = -\frac{3\pi}{4}, -\frac{\pi}{2}, -\frac{\pi}{4}, \frac{\pi}{4}, \frac{\pi}{2}, \frac{3\pi}{4} \).
La derivata prima di \( f(x) = \sin(x) + \frac{1}{3}\sin(3x) \) è \( f'(x) = \cos(x) + \cos(3x) = 2\cos(2x)\cos(x) \).
La disequazione \( 2\cos(2x)\cos(x) > 0 \) è soddisfatta quando \( \cos(x) \) e \( \cos(2x) \) hanno lo stesso segno.
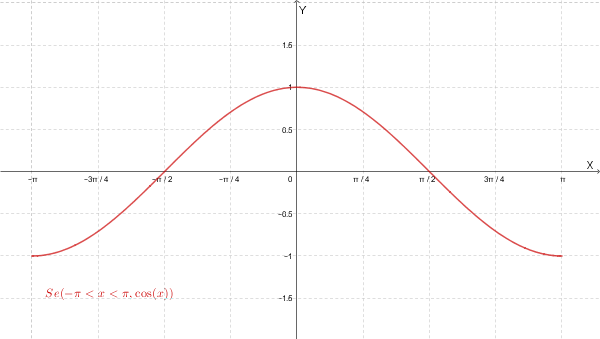
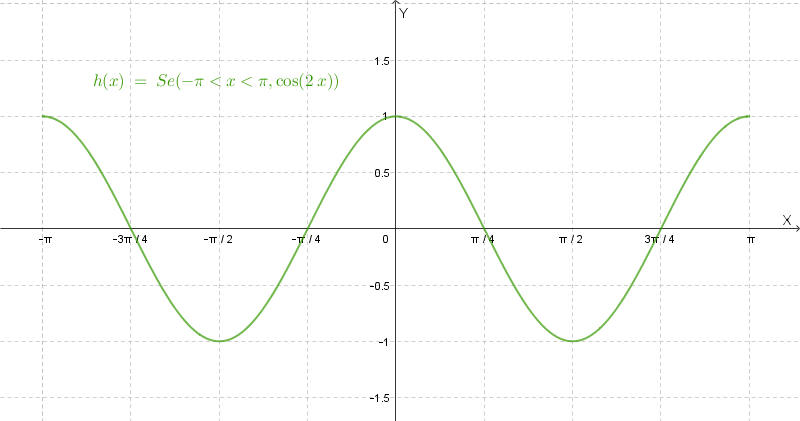
Guardando il seguente grafico e combinando i segni, \( f'(x) > 0 \) quando:
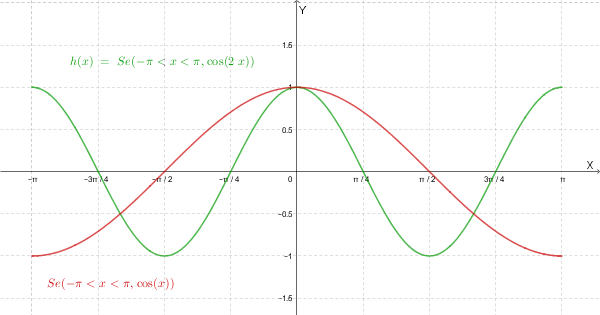
Quindi la disequazione \( 2\cos(2x)\cos(x) > 0 \) è soddisfatta per \( x \in (-\frac{3\pi}{4}, -\frac{\pi}{2}) \cup (-\frac{\pi}{4}, \frac{\pi}{4}) \cup (\frac{\pi}{2}, \frac{3\pi}{4}) \).
| Intervallo | Segno di \( \cos(x) \) | Segno di \( \cos(2x) \) | Segno di \( f'(x) \) | Monotonia |
|---|---|---|---|---|
| \( -\pi < x < -\frac{3\pi}{4} \) | - | + | - | Decrescente |
| \( -\frac{3\pi}{4} < x < -\frac{\pi}{2} \) | - | - | + | Crescente |
| \( -\frac{\pi}{2} < x < -\frac{\pi}{4} \) | - | + | - | Decrescente |
| \( -\frac{\pi}{4} < x < \frac{\pi}{4} \) | + | + | + | Crescente |
| \( \frac{\pi}{4} < x < \frac{\pi}{2} \) | + | - | - | Decrescente |
| \( \frac{\pi}{2} < x < \frac{3\pi}{4} \) | - | - | + | Crescente |
| \( \frac{3\pi}{4} < x < \pi \) | - | + | - | Decrescente |
Partendo dalla funzione \( f(x) = \sin(x) + \frac{1}{3}\sin(3x) \), calcoliamo la derivata prima:
\( f'(x) = \frac{d}{dx}(\sin(x)) + \frac{1}{3}\frac{d}{dx}(\sin(3x)) = \cos(x) + \frac{1}{3}(3\cos(3x)) = \cos(x) + \cos(3x) \).
Ora deriviamo la derivata prima per ottenere la derivata seconda:
\( f''(x) = \frac{d}{dx}(\cos(x)) + \frac{d}{dx}(\cos(3x)) = -\sin(x) - 3\sin(3x) \).
Utilizzando la formula dell'angolo triplo \( \sin(3x) = 3\sin(x) - 4\sin^3(x) \), otteniamo:
\( f''(x) = -\sin(x) - 3(3\sin(x) - 4\sin^3(x)) = -\sin(x) - 9\sin(x) + 12\sin^3(x) = 12\sin^3(x) - 10\sin(x) \).
Fattorizzando \( 2\sin(x) \), arriviamo a:
La derivata seconda di \( f(x) = \sin(x) + \frac{1}{3}\sin(3x) \) è \( f''(x) = 2\sin(x)(6\sin^2(x) - 5) \).
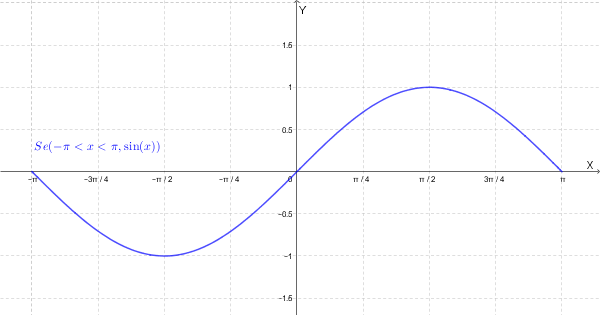
Utilizzando l'identità \( \cos(2x) = 1 - 2\sin^2(x) \), possiamo ricavare \( \sin^2(x) = \frac{1 - \cos(2x)}{2} \).
Sostituendo nell'espressione \( 6\sin^2(x) - 5 \):
\( 6\sin^2(x) - 5 = 6 \left( \frac{1 - \cos(2x)}{2} \right) - 5 = 3(1 - \cos(2x)) - 5 = 3 - 3\cos(2x) - 5 = -3\cos(2x) - 2 \).
Quindi, studiare il segno di \( 6\sin^2(x) - 5 \) è equivalente a studiare il segno di \( -3\cos(2x) - 2 \).
Quindi, studiare il segno di \( 6\sin^2(x) - 5 \) è equivalente a studiare il segno di \( -3\cos(2x) - 2 \).
Questo grafico può essere dedotto dal grafico di \( y=\cos(x) \) mediante trasformazioni geometriche elementari:
1) Da \( y=\cos(x) \) a \( y=\cos(2x) \): contrazione orizzontale di fattore 2.
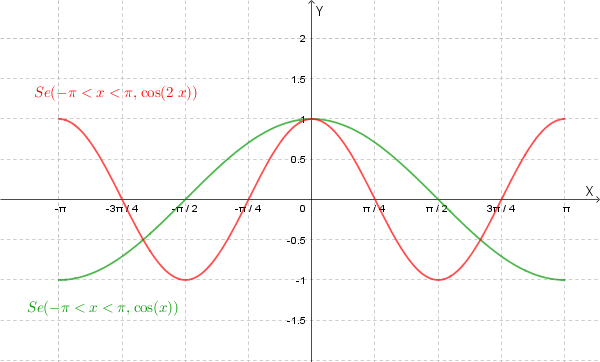
2) Da \( y=\cos(2x) \) a \( y =3\cos(2x) \): dilatazione verticale di fattore 3:
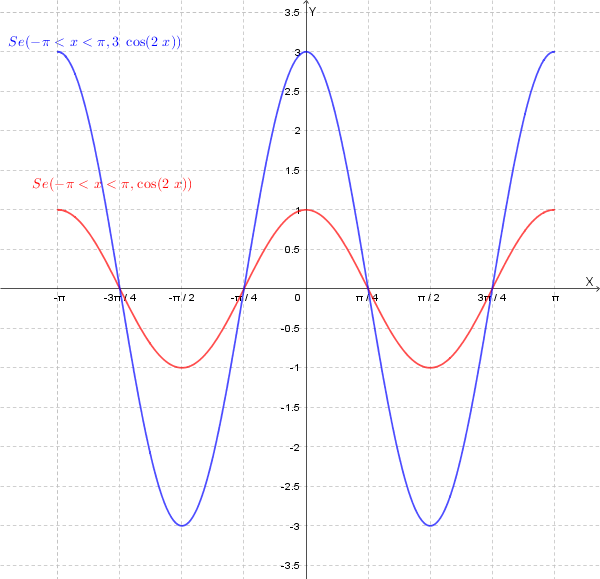
3) Da \( y=3\cos(2x) \) a \( y=-3\cos(2x) \): simmetria rispetto all'asse delle x.
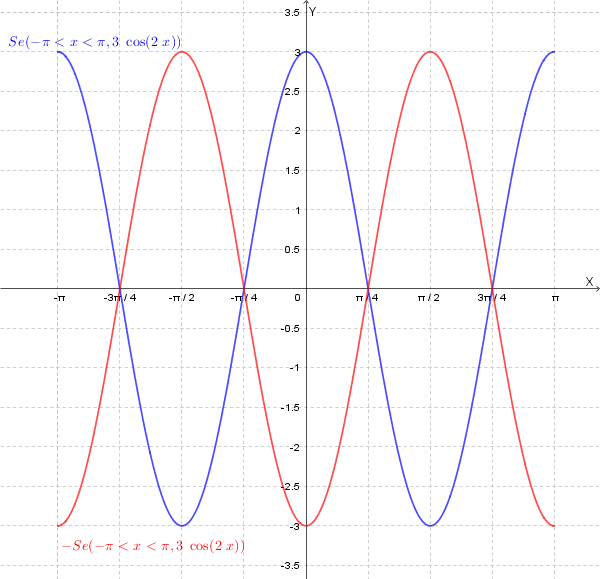
4) Da \( y= -3\cos(2x) \) a \( y=-3\cos(2x)-2 \): traslazione di vettore \( \mathbf{v}=(0,-2) \).
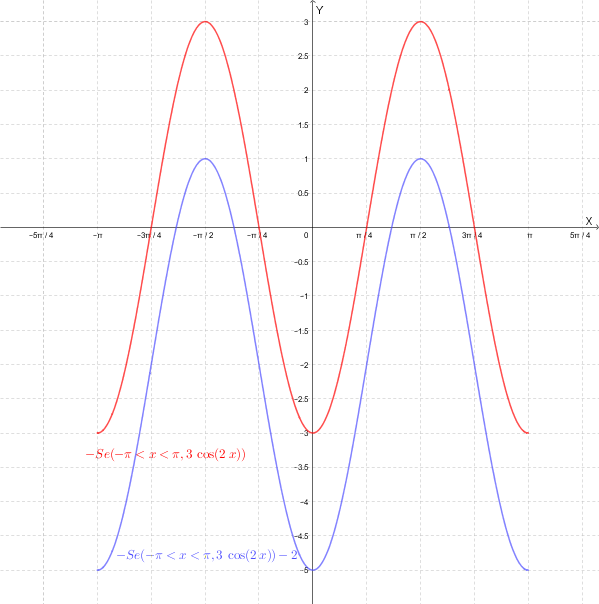
Quindi il grafico di \( 6\sin^2(x) - 5 \), che è uguale al grafico di \( -3\cos(2x) - 2 \) è il seguente:
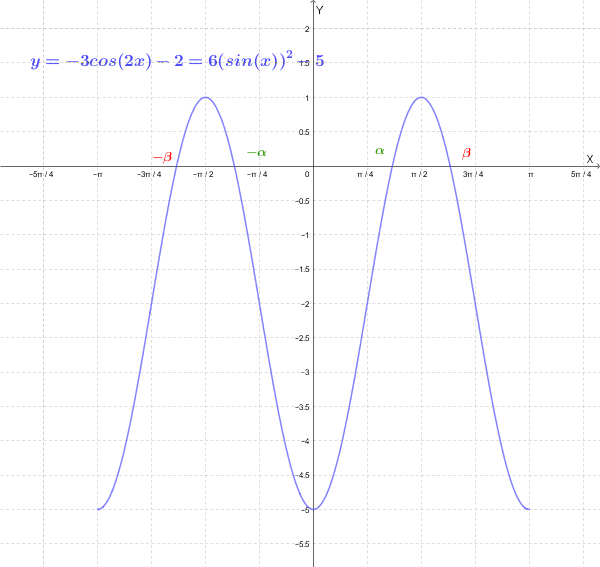
Per studiare il segno della derivata seconda rappresentiamo nello stesso piano cartesiano i grafici di \( y=\sin(x) \) e di \( y=6\sin^2(x) - 5 \)
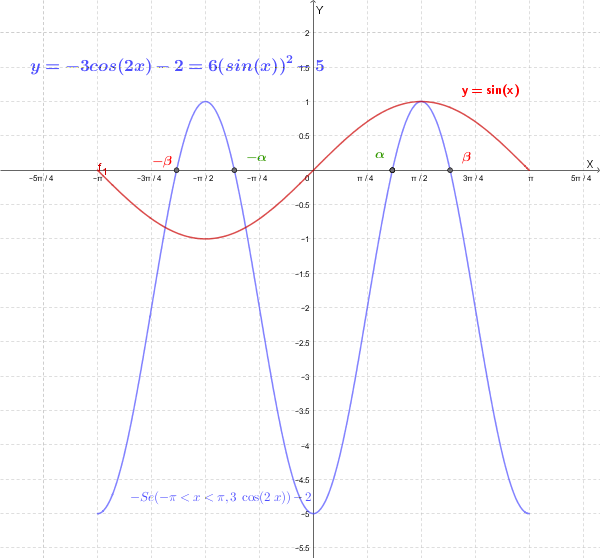
Siano \( \alpha = \arcsin(\sqrt{5/6}) \approx 1.15 \) e \( \beta = \pi - \arcsin(\sqrt{5/6}) \approx 1.99 \).
| Intervallo | Segno di \( \sin(x) \) | Segno di \( 6\sin^2(x) - 5 \) | Segno di \( f''(x) \) |
|---|---|---|---|
| \( -\pi < x < -\beta \) | - | - | + |
| \( -\beta < x < -\alpha \) | - | + | - |
| \( -\alpha < x < 0 \) | - | - | + |
| \( 0 < x < \alpha \) | + | - | - |
| \( \alpha < x < \beta \) | + | + | + |
| \( \beta < x < \pi \) | + | - | - |
La funzione è concava verso l'alto (\( f''(x) > 0 \)) negli intervalli:
La funzione \( f(x) = x + \sin(x) \) è considerata nell'intervallo specificato:
\[ \boxed{D = [-3\pi, 3\pi]} \]
Per verificare la parità, calcoliamo \( f(-x) \):
\( f(-x) = -x + \sin(-x) = -x - \sin(x) = -(x + \sin(x)) = -f(x) \).
Poiché \( f(-x) = -f(x) \), la funzione è dispari. Questa proprietà vale su tutto il dominio \( \mathbb{R} \), e quindi anche sull'intervallo \( [-3\pi, 3\pi] \), che è simmetrico rispetto all'origine.
Asse x (y=0):
\( x + \sin(x) = 0 \implies \sin(x) = -x \).
Oltre alla soluzione in \( x = 0 \), analizzando graficamente l'intersezione tra \( y = \sin(x) \) e \( y = -x \) nell'intervallo \( [-3\pi, 3\pi] \), si nota che l'unica intersezione si verifica in \( x = 0 \).
![Grafico di \( y = \sin(x) \) e \( y = -x \) in \( [-3\pi, 3\pi] \)](graph4-intersezioni.png)
L'unica intersezione con l'asse x è in \( x = 0 \), quindi il punto è \( (0, 0) \).
Asse y (x=0):
\( f(0) = 0 + \sin(0) = 0 \).
L'intersezione con l'asse y è in \( y = 0 \), quindi il punto è \( (0, 0) \).
Il segno della funzione \( f(x) = x + \sin(x) \) nell'intervallo \( [-3\pi, 3\pi] \) dipende dalla relazione tra \( x \) e \( -\sin(x) \).
Dal grafico si evidenzia che \( \sin(x) > -x \) per \( x > 0 \) e \( \sin(x) < -x \) per \( x < 0 \) (escluso \( x=0 \)). Pertanto, la funzione è positiva per \( x > 0 \) e negativa per \( x < 0 \) nell'intervallo considerato.
![Grafico di \( y = x + \sin(x) \) in \( [-3\pi, 3\pi] \)](graph4-intersezioni.png)
Poiché stiamo considerando un intervallo chiuso \( [-3\pi, 3\pi] \), non è necessario calcolare i limiti a \( \pm\infty \). La funzione è continua in questo intervallo.
Valori agli estremi dell'intervallo:
Poiché stiamo considerando un intervallo chiuso \( [-3\pi, 3\pi] \), non ci sono asintoti all'interno di questo intervallo. La funzione è continua.
\[ f'(x) = 1 + \cos(x) \]
Studio del segno di \( f'(x) \) nell'intervallo \( [-3\pi, 3\pi] \):
La funzione è crescente sull'intervallo \( [-3\pi, 3\pi] \), con punti di tangente orizzontale in \( x = -3\pi, -\pi, \pi, 3\pi \).
\[ f''(x) = -\sin(x) \]
Studio del segno di \( f''(x) \) nell'intervallo \( [-3\pi, 3\pi] \):
Punti di flesso in \( x = -3\pi, -2\pi, -\pi, 0, \pi, 2\pi, 3\pi \). L'ordinata dei punti di flesso è \( f(k\pi) = k\pi + \sin(k\pi) = k\pi \) per \( k = -3, -2, -1, 0, 1, 2, 3 \).
N.B.
Osserviamo che nei punti di flesso \( \sin(x) \) si annulla, quindi le coordinate dei punti di flesso \( (k\pi, f(k\pi)) = (k\pi, k\pi + \sin(k\pi)) \) diventano \( (k\pi, k\pi) \). Questo significa che i punti di flesso soddisfano l'equazione \( y = x \). In altre parole, i flessi appartengono alla retta \( y = x \).
Dimostrare che i flessi giacciono sulla retta \( y = x \) fornisce un'ulteriore conferma visiva di come la componente sinusoidale perturba la semplice retta \( y = x \), creando le ondulazioni caratteristiche, ma mantenendo i punti di inflessione allineati con essa.